RSA Beginner

Se nos proporcionan estos números:

e: 3
c: 174422460809195453539354885823735245900172562989776845322302
n: 245841236512478852752909734912575581815967630033049838269083

Tenemos el exponente , el módulo y el texto cifrado .

Está claro que estamos ante un criptosistema RSA. Vamos a recordar cómo funciona RSA:

Se eligen dos números primos y de forma que el módulo . Luego se escoge un exponente (normalmente 3 ó 65537) que sea coprimo con .

Para cifrar un mensaje (en formato numérico), se tiene que realizar esta operación:

Donde es el texto cifrado. Y para descifrar el texto cifrado, tenemos que calcular y luego realizar la siguiente operación:

En este punto, la clave pública es el conjunto , mientras que la clave privada está compuesta por .

El criptosistema RSA será robusto en función de la dificultad para factorizar el módulo . Si se pudiera factorizar, se podrían obtener y a partir de y por tanto calcular y .

Esta vez, el ódulo que tenemos es relativamente pequeño, por lo que podremos factorizarlo. Para ello, podemos ir a factordb.com e introducir el módulo:

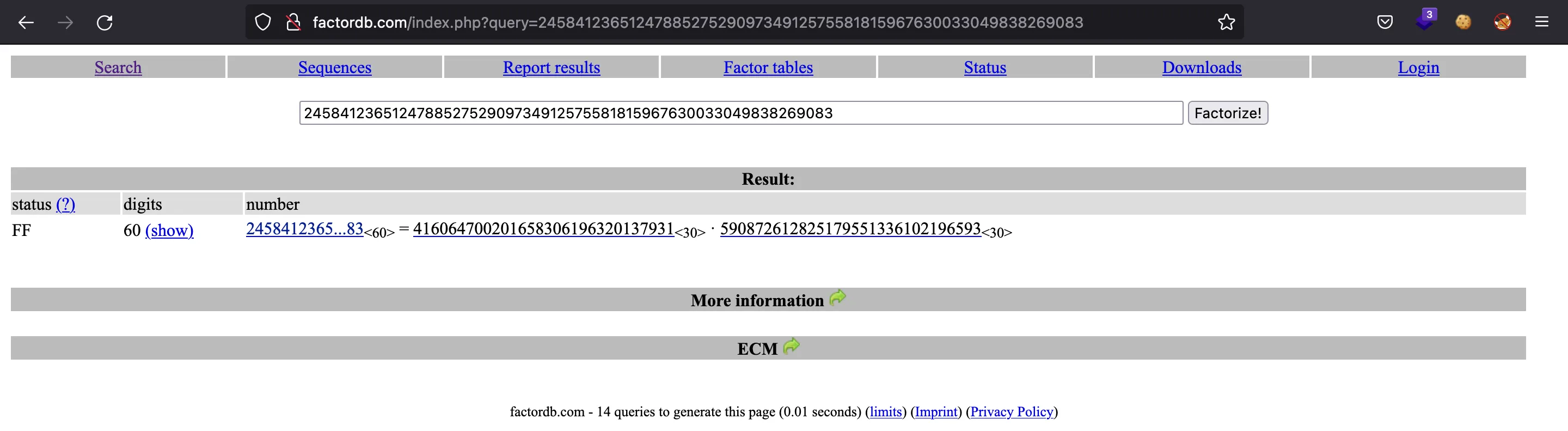
Y ahora que tenemos y , podemos usar Python para calcular y . Y finalmente hallar el mensaje :

$ python3 -q
>>> e = 3
>>> c = 174422460809195453539354885823735245900172562989776845322302
>>> n = 245841236512478852752909734912575581815967630033049838269083
>>> p = 416064700201658306196320137931
>>> q = 590872612825179551336102196593
>>> phi_n = (p - 1) * (q - 1)
>>> d = pow(e, -1, phi_n)
>>> m = pow(c, d, n)
>>> hex(m)
'0x4354466c6561726e7b7273345f69735f61773373306d337d'

El mensaje está en formato numérico, por lo que tenemos que decodificarlo como bytes en ASCII:

>>> bytes.fromhex('4354466c6561726e7b7273345f69735f61773373306d337d')
b'CTFlearn{rs4_is_aw3s0m3}'