Branching Tactics
5 minutos de lectura
Se nos proporciona una instancia remota a la que conectarnos:
$ nc 94.237.49.212 45041
You have a set of troops tasked with placing tnt in the underground tunnel. For every scenario, you will have the below values:
1. The n number of nodes in the terrain, where 2 <= n <= 3 * 10 ** 5.
2. The following n-1 lines will have 2 numbers e1, e2. These will both be nodes of the tunnels, where 1 <= e1, e2 <= n. The pair of nodes e1, e2 are connected.
3. The next number is m, the number of troops carrying tnt, where 1 <= m <= n.
4. m lines will follow, each with 3 values: s (the starting node of the troop), d (the destination node of the troop), and e (the energy of the troop), where 1 <= s, d, e <= n.
Each troop does their best job to move from nodes s to d, but can only make a maximum of e movements between nodes. The troop tries to get as far as possible with what energy it has.
Each movement from one node to another costs 1 energy, decreasing e by 1 - once e is at 0, the troop can not make another move.
Find the node each troop ends up in and place the tnt. Send the node e, in the same order as you received the s-d-e triplets.
Example Scenario:
3
3 2
2 1
2
1 1 1
1 3 1
Example Response:
1
2
Test 1/100
2
1 2
1
1 2 2
Planteamiento del problema
En este desafío, debemos programar un algoritmo para resolver el problema anterior un total de 100 veces. En cada ronda, se nos da un grafo con
Necesitamos saber a qué nodo llegará la tropa cuando se quede sin pasos
Búsqueda en anchura
Uno de los algoritmos más apropiados para encontrar el camino más corto es el de búsqueda en anchura (BFS, Breadth-first Search). Básicamente, este algoritmo comienza desde un nodo raíz del grafo, lo marca como visitado, toma los nodos adyacentes y los pone en una cola. Luego, iterativamente, para cada nodo en la cola, lo marca como visitado y encuentra los nodos adyacentes y los inserta en la cola. Este proceso continúa hasta llegar al destino deseado, que será el camino más corto:
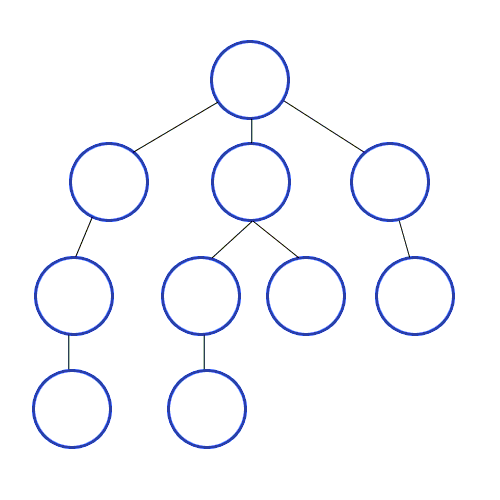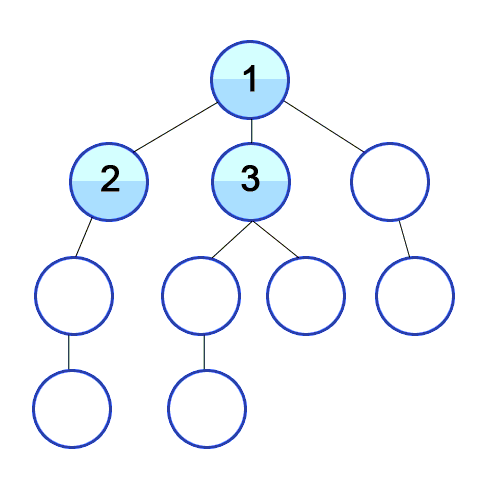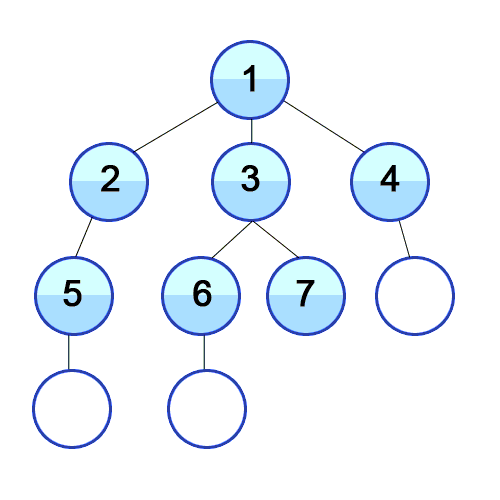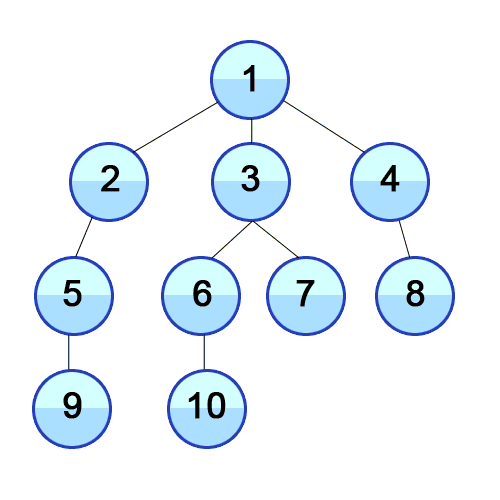
Fuente: https://commons.wikimedia.org/wiki/File:Breadth-First-Search-Algorithm.gif
Implementación
Este algoritmo se puede implementar muy fácilmente en Go:
type path struct {
node int
path []int
}
func bfs(s, d int, edges map[int][]int) []int {
queue := []path{{node: s, path: []int{s}}}
visited := map[int]bool{}
for len(queue) > 0 {
n := queue[0]
queue = queue[1:]
visited[n.node] = true
if n.node == d {
return n.path
}
for _, v := range edges[n.node] {
if !visited[v] {
queue = append(queue, path{node: v, path: slices.Concat(n.path, []int{v})})
}
}
}
return []int{}
}
Observe que utilicé una estructura path para guardar el nodo actual y la ruta hasta ese nodo. Por lo tanto, cuando lleguemos al destino, devolveremos el camino, que será el más corto.
Para resolver el reto, solo necesitamos ver si la tropa puede llegar al destino en
func solve(s, d, e int, edges map[int][]int) int {
path := bfs(s, d, edges)
if e >= len(path) {
return d
} else {
return path[e]
}
}
Por último, pero no menos importante, esta es la función main, que utiliza mi módulo gopwntools para analizar la información enviada por la instancia remota en cada ronda y luego llama a solve para devolver las soluciones:
func main() {
hostPort := strings.Split(os.Args[1], ":")
io := pwn.Remote(hostPort[0], hostPort[1])
defer io.Close()
prog := pwn.Progress("Round")
for range 100 {
io.RecvUntil([]byte("Test"))
prog.Status(strings.TrimSpace(io.RecvLineS()))
n, _ := strconv.Atoi(strings.TrimSpace(io.RecvLineS()))
edges := map[int][]int{}
for i := 0; i < n-1; i++ {
e1, _ := strconv.Atoi(strings.TrimSpace(io.RecvUntilS([]byte{' '})))
e2, _ := strconv.Atoi(strings.TrimSpace(io.RecvLineS()))
edges[e1] = append(edges[e1], e2)
edges[e2] = append(edges[e2], e1)
}
m, _ := strconv.Atoi(strings.TrimSpace(io.RecvLineS()))
for i := 0; i < m; i++ {
s, _ := strconv.Atoi(strings.TrimSpace(io.RecvUntilS([]byte{' '})))
d, _ := strconv.Atoi(strings.TrimSpace(io.RecvUntilS([]byte{' '})))
e, _ := strconv.Atoi(strings.TrimSpace(io.RecvLineS()))
res := solve(s, d, e, edges)
io.SendLine([]byte(strconv.Itoa(res)))
}
}
prog.Success("100/100")
io.RecvUntil([]byte("HTB{"))
pwn.Success("HTB{" + io.RecvLineS())
}
Flag
Si ejecutamos el script anterior, obtendremos la flag:
$ go run solve.go 94.237.49.212:45041
[+] Opening connection to 94.237.49.212 on port 45041: Done
[+] Round: 100/100
[+] HTB{tReE_tR3e_4nD_Tr33_aG4iN!}
[*] Closed connection to 94.237.49.212 port 45041
Como se puede observar, la flag habla sobre árboles (tree), que es una estructura de datos muy común en los retos de programación. Hay algoritmos mejores para resolver este reto, como el ancestro común más bajo (LCA, Least Common Ancestor). Sin embargo, la descripción del problema no fue lo suficientemente clara para mí para poder asumir que todos los grafos eran árboles. Por ejemplo, aunque el grafo tenga
El script completo se puede encontrar aquí: solve.go.