Path of Survival
4 minutos de lectura
Se nos proporciona el siguiente sitio web:
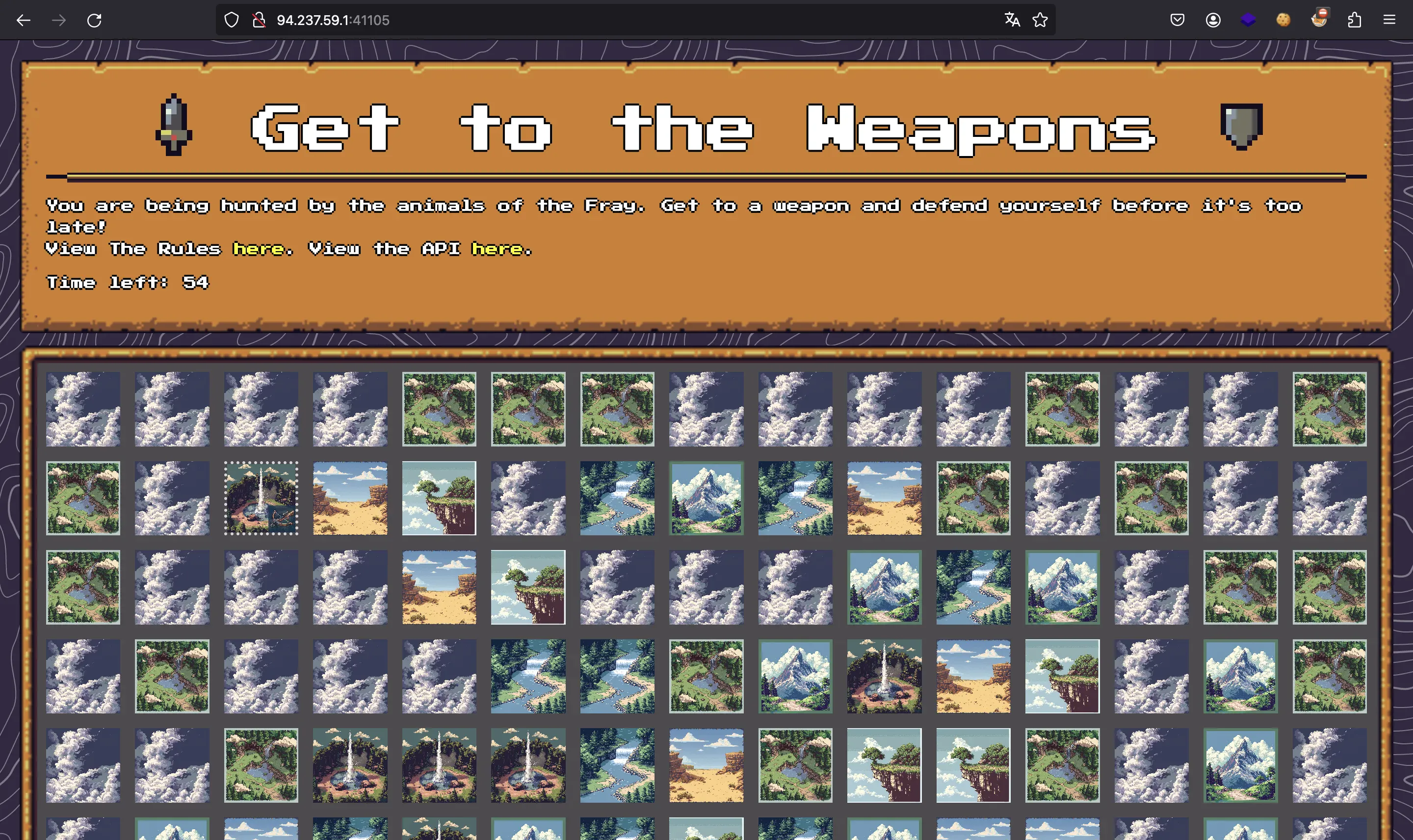
Muestra una especie de laberinto en el que somos un astronauta y necesitamos encontrar un arma en el menor tiempo posible.
El sitio web muestra cómo interactuar con nuestro jugador astronauta y muestra algunas reglas con respecto a las casillas del laberinto. (Cliff, Geyser, Mountain…):
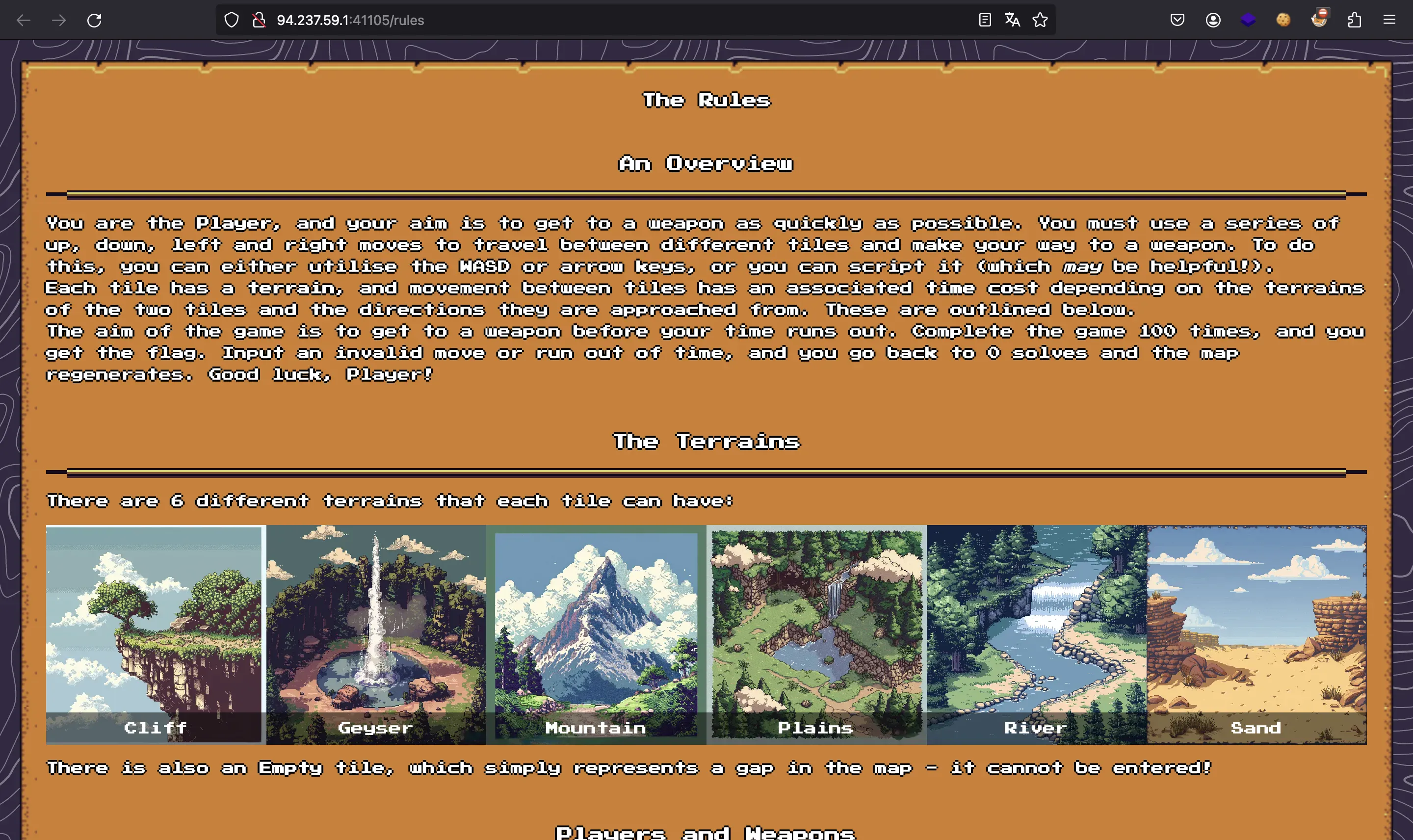
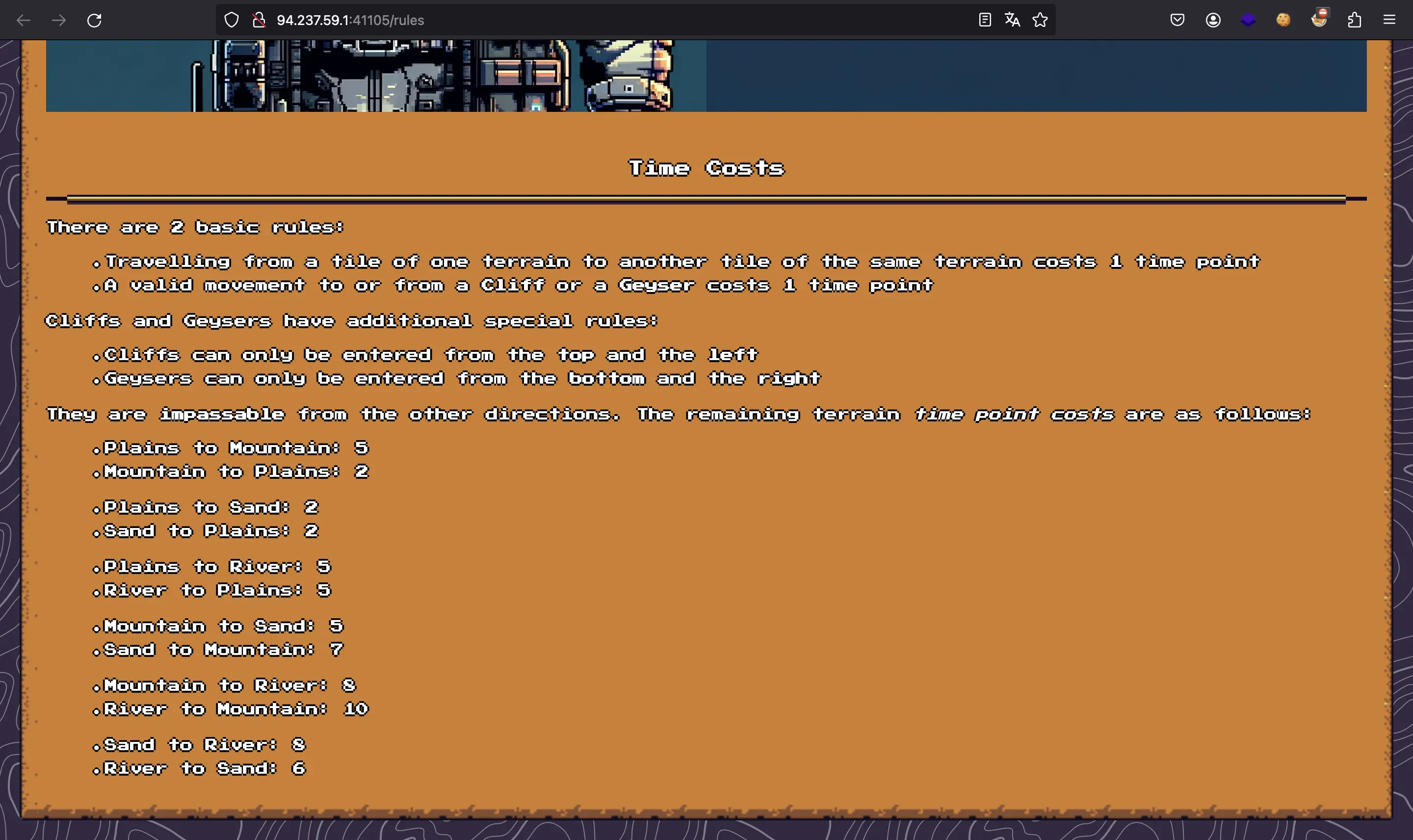
Además, tenemos una API HTTP para obtener el mapa como documento JSON y ejecutar comandos para mover el astronauta:
Path-finding
El algoritmo más adecuado para encontrar un arma en el mapa en el menor tiempo posible es el algoritmo de Dijkstra. Este algoritmo consiste en construir un grafo ponderado donde los nodos son las casillas del mapa y las aristas son las conexiones directas entre las casillas, con su coste de tiempo correspondiente.
Una vez que se completa el grafo, el algoritmo toma el origen y actualiza todos los costes a todas las posiciones del grafo, de modo que tenemos el tiempo necesario para llegar a cualquier casilla del mapa. Finalmente, podemos buscar un arma en el mapa que podamos alcanzar dentro del límite de tiempo establecido por el reto.
Búsqueda en anchura
Sin embargo, utilicé otro algoritmo de path-finding llamado búsqueda en anchura (BFS, Breadth-first Search), porque estoy más acostumbrado.
Básicamente, este algoritmo comienza desde un nodo raíz del grafo, lo marca como visitado, toma los nodos adyacentes y los pone en una cola. Luego, iterativamente, para cada nodo en la cola, lo marca como visitado y encuentra los nodos adyacentes y los inserta en la cola. Este proceso continúa hasta llegar al destino deseado, que será el camino más corto:
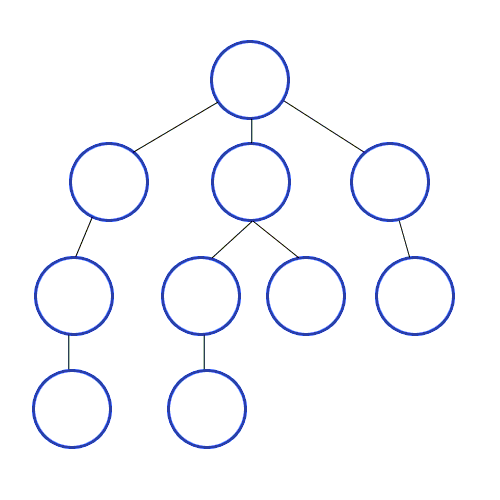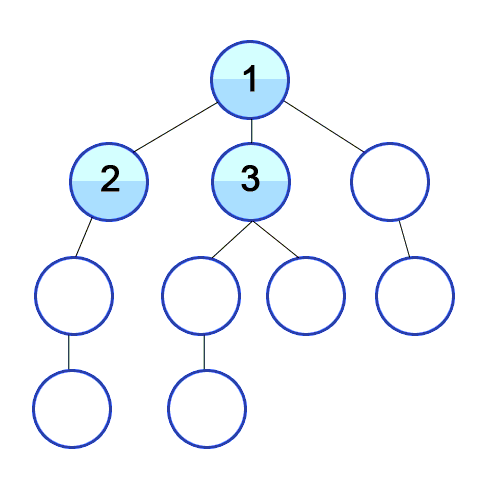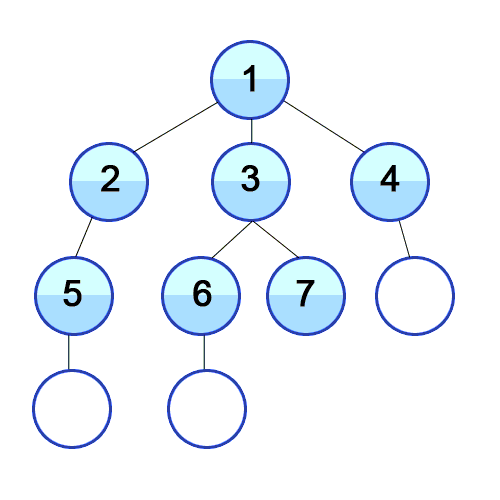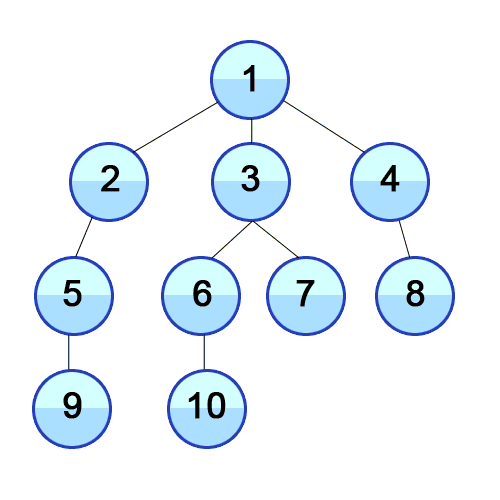
Fuente: https://commons.wikimedia.org/wiki/File:Breadth-First-Search-Algorithm.gif
Implementación
En primer lugar, necesitamos descargar el mapa y procesarlo. Para esto, definiremos tres funciones auxiliares para interactuar con la API:
def get_map():
map_data = requests.post(f'{URL}/map').json()
time = map_data.get('player').get('time')
orig_coords = tuple(map_data.get('player').get('position'))
orig = orig_coords[0] + 1j * orig_coords[1]
weapons = set()
map_tiles = {}
for coord, tile_data in map_data.get('tiles').items():
if tile_data.get('has_weapon'):
dest_coords = ast.literal_eval(coord)
weapons.add(dest_coords[0] + 1j * dest_coords[1])
x, y = ast.literal_eval(coord)
map_tiles[x + 1j * y] = tile_data.get('terrain')
return map_tiles, orig, weapons, time
def update(direction):
return requests.post(f'{URL}/update', json={'direction': direction}).json()
def regenerate():
requests.get(f'{URL}/regenerate')
La parte principal del script de solución es el algoritmo BFS:
def bfs(root, map_tiles):
queue = deque([root])
visited_states = {(root, time)}
while len(queue):
pos, time_left, path = queue.popleft()
if time_left < 0:
continue
if (current_tile := map_tiles.get(pos)) is None:
continue
next_pos = [pos - 1, pos + 1, pos - 1j, pos + 1j]
for n in next_pos:
tile = map_tiles.get(n, 'E')
if tile == 'E':
continue
if tile == 'G' and n - pos in {1, 1j}:
continue
if tile == 'C' and n - pos in {-1, -1j}:
continue
new_time = time_left - terrain_costs.get(current_tile + tile, math.inf)
if new_time >= 0:
if n in weapons:
return path + (n, ), time_left
if (n, new_time) not in visited_states:
queue.append((n, new_time, path + (n, )))
visited_states.add((n, new_time))
return (), 0
El código anterior es bastante estándar, usando collections.deque por cuestiones de rendimiento, aunque necesitamos agregar el tiempo que queda a los nodos visitados en caso de que podamos alcanzar un nodo en menos tiempo. Además, obsérvese cómo consideré casillas vacías, Geyser y Cliff.
Ya que estamos usando Python, las coordenadas
Para conocer los costes entre las casillas, utilicé un diccionario donde la primera letra representa el origen y la segunda letra representa el destino:
terrain_costs = {
'PM': 5, 'MP': 2,
'PS': 2, 'SP': 2,
'PR': 5, 'RP': 5,
'MS': 5, 'SM': 7,
'MR': 8, 'RM': 10,
'SR': 8, 'RS': 6,
'PP': 1, 'MM': 1,
'SS': 1, 'RR': 1,
'CC': 1, 'GG': 1,
'PC': 1, 'CP': 1,
'MC': 1, 'CM': 1,
'SC': 1, 'CS': 1,
'RC': 1, 'CR': 1,
'GC': 1, 'CG': 1,
'PG': 1, 'GP': 1,
'MG': 1, 'GM': 1,
'SG': 1, 'GS': 1,
'RG': 1, 'GR': 1,
}
DIRECTIONS = {-1: 'L', 1: 'R', -1j: 'U', 1j: 'D'}
Finalmente, necesitamos ejecutar el algoritmo 100 veces para obtener la flag:
regenerate()
rounds = 1
round_prog = log.progress('Round')
while rounds <= 100:
map_tiles, orig, weapons, time = get_map()
root = (orig, time, (orig, ))
path, time_left = bfs(root, map_tiles)
round_prog.status(f'{rounds} / 100')
if not path and not time_left:
regenerate()
round_prog.failure('No path found')
round_prog = log.progress('Round')
rounds = 1
continue
path_tiles = list(map(map_tiles.get, path))
prev = orig
for coord in path[1:]:
direction = DIRECTIONS.get(coord - prev, '?')
data = update(direction)
prev = coord
if data.get('error'):
round_prog.failure(data)
round_prog = log.progress('Round')
rounds = 1
break
if (flag := data.get('flag')):
log.success(f'Flag: {flag}')
round_prog.success('100 / 100')
else:
rounds += 1
Flag
Si ejecutamos el script anterior, eventualmente obtendremos la flag:
$ python3 solve.py 94.237.59.1:41105
[+] Round: 100 / 100
[+] Flag: HTB{dIjKStr4_m4estRa_y0U_c4n_f1nD_tH3_p4Th!!!}
El script completo se puede encontrar aquí: solve.py.