<- MISC

Quantum Artifact

9 minutos de lectura

Se nos proporciona el siguiente código fuente en Python que codifica la flag:

from qiskit import *
import qiskit.qasm2

flag = open('flag.txt', 'rb').read()
secret = ''.join("{0:08b}".format(c) for c in flag)
circuit = QuantumCircuit(len(secret)+1, len(secret))

circuit.h(range(len(secret)))
circuit.x(len(secret))
circuit.h(len(secret))

circuit.barrier()

for ii, yesno in enumerate(reversed(secret)): 
    if yesno == '1':
        circuit.cx(ii, len(secret))

circuit.barrier()

circuit.h(range(len(secret)))
circuit.barrier()
circuit.measure(range(len(secret)), range(len(secret)))

qasm_code = qiskit.qasm2.dumps(circuit)

# Write the OpenQASM code to a file
with open('challenge_circuit.qasm', 'w') as file:
    file.write(qasm_code)

También se nos proporciona el circuito cuántico serializado como challenge_circuit.qasm.

Análisis del código fuente

Como se puede ver, el circuito cuántico consiste en varios registros de qbits, específicamente, uno más que la longitud de la flag en binario, y registros de bits clásicos, exactamente de la longitud de la flag en binario:

flag = open('flag.txt', 'rb').read()
secret = ''.join("{0:08b}".format(c) for c in flag)
circuit = QuantumCircuit(len(secret)+1, len(secret))

Podemos comprobar esto importando el circuito cuántico y observando algunos atributos:

$ python3 -q
>>> from qiskit import QuantumCircuit
>>> 
>>> circuit = QuantumCircuit.from_qasm_file('challenge_circuit.qasm')
>>> 
>>> circuit.num_qubits
233
>>> circuit.num_clbits
232

Así que sabemos que la flag está compuesta por 232 bits. El servidor agrega una puerta Hadamard a todos estos qbits de la flag:

circuit.h(range(len(secret)))

Luego, el servidor agrega una puerta Pauli X y una puerta Hadamard al último qbit:

circuit.x(len(secret))
circuit.h(len(secret))

Aquí, el servidor agrega una barrera para separar etapas (no ocurre nada en el circuito cuántico, es solo para mejorar la legibilidad):

circuit.barrier()

Después de eso, el servidor comienza a codificar los bits de la flag en el circuito cuántico:

for ii, yesno in enumerate(reversed(secret)): 
    if yesno == '1':
        circuit.cx(ii, len(secret))

Como se puede ver, los bits se iteran en orden inverso, y si el bit es 1, el servidor agrega una puerta CX (X controlada, también conocida como CNOT) entre el qbit de la flag correspondiente (control) y el último qbit (objetivo).

Después de una segunda barrera, el servidor agrega otra puerta Hadamard a todos los qbits de la flag:

circuit.barrier()

circuit.h(range(len(secret)))

Finalmente, tras una tercera barrera, el servidor agrega mediciones para leer el valor de los qbits de la flag y escribirlos en los registros de bits clásicos correspondientes:

circuit.barrier()
circuit.measure(range(len(secret)), range(len(secret)))

Solución

Hay dos formas de resolver este reto:

La forma fácil

Incluso si no sabemos nada sobre computación cuántica, sabemos que hay una puerta CX siempre que el bit de la flag es 1. Por lo tanto, podemos echar un vistazo a las instrucciones del circuito:

>>> print('\n'.join(map(str, circuit.get_instructions('cx'))))
CircuitInstruction(operation=Instruction(name='cx', num_qubits=2, num_clbits=0, params=[]), qubits=(<Qubit register=(233, "q"), index=0>, <Qubit register=(233, "q"), index=232>), clbits=())
CircuitInstruction(operation=Instruction(name='cx', num_qubits=2, num_clbits=0, params=[]), qubits=(<Qubit register=(233, "q"), index=2>, <Qubit register=(233, "q"), index=232>), clbits=())
CircuitInstruction(operation=Instruction(name='cx', num_qubits=2, num_clbits=0, params=[]), qubits=(<Qubit register=(233, "q"), index=3>, <Qubit register=(233, "q"), index=232>), clbits=())
...
CircuitInstruction(operation=Instruction(name='cx', num_qubits=2, num_clbits=0, params=[]), qubits=(<Qubit register=(233, "q"), index=222>, <Qubit register=(233, "q"), index=232>), clbits=())
CircuitInstruction(operation=Instruction(name='cx', num_qubits=2, num_clbits=0, params=[]), qubits=(<Qubit register=(233, "q"), index=227>, <Qubit register=(233, "q"), index=232>), clbits=())
CircuitInstruction(operation=Instruction(name='cx', num_qubits=2, num_clbits=0, params=[]), qubits=(<Qubit register=(233, "q"), index=230>, <Qubit register=(233, "q"), index=232>), clbits=())

Obsérvese que la puerta CX involucra dos qbits, el qbit de control y el qbit objetivo. Nos interesa tomar el índice del qbit de control, lo cual se puede hacer así:

>>> [i.qubits[0]._index for i in circuit.get_instructions('cx')]
[0, 2, 3, 4, 5, 6, 8, 9, 12, 13, 20, 21, 22, 28, 29, 35, 37, 38, 40, 41, 42, 43, 44, 46, 48, 49, 52, 53, 56, 58, 59, 61, 62, 68, 69, 72, 73, 76, 77, 78, 80, 81, 82, 83, 84, 86, 90, 91, 93, 94, 98, 99, 101, 102, 104, 108, 109, 114, 116, 117, 118, 120, 121, 124, 125, 126, 128, 129, 130, 131, 132, 134, 136, 137, 140, 141, 142, 144, 148, 149, 152, 153, 154, 155, 156, 158, 160, 161, 164, 165, 169, 172, 173, 174, 176, 177, 180, 181, 187, 189, 190, 194, 196, 197, 198, 200, 201, 203, 204, 205, 206, 209, 214, 218, 220, 222, 227, 230]

Ahora solo queda establecer un 1 o un 0 dependiendo de si el índice de la flag aparece o no en la lista anterior:

>>> ''.join(map(str, (int(x in [i.qubits[0]._index for i in circuit.get_instructions('cx')]) for x in reversed(range(circuit.num_qubits - 1)))))
'0100100001010100010000100111101101110100011010000011001101110010001100110101111100110001011100110101111101110011011101000011000101101100011011000101111101110011001100000110110100110011010111110110100000110000011100000011001101111101'

Luego, simplemente convertimos la cadena binaria anterior a bytes y listo, aunque no habremos aprendido nada sobre computación cuántica.

Fundamentos de computación cuántica

Voy a dar algo de contexto sobre computación cuántica y puertas cuánticas:

  • En computación cuántica, los qbits no tienen un valor cierto, tienen un estado de superposición. Esto significa que pueden tener cualquier valor hasta que se mida el qbit. Una vez que se observa un qbit, colapsa a un valor (0 ó 1) y no puede cambiarse. Y esto ocurre con cierta probabilidad, que se puede expresar como , donde y representan la probabilidad de colapsar a 0 ó 1, por lo tanto

  • Una puerta Hadamard (H) produce un “cambio de base”:

  • Medir un qbit que ha sido transformado por una puerta Hadamard tiene un 50% de probabilidad de colapsar a 0 ó a 1

  • La puerta Pauli X se comporta de la siguiente manera:

  • En particular

  • La puerta CX involucra dos qbits: el qbit de control y el qbit objetivo. Si el qbit de control está en , se realiza la operación X sobre el qbit objetivo. En particular:

  • Una aplicación directa de la puerta CX (también conocida como CNOT) es el estado de Bell, que es una forma de entrelazamiento cuántico:

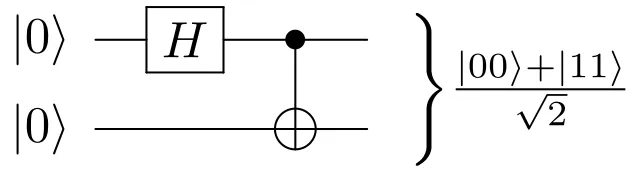
two-wrongs 1

El circuito anterior tiene 3 estados diferentes:

  • Estado inicial:

  • Tras la puerta H:

  • Tras la puerta CX:

En este punto, ambos qbits están entrelazados, lo que significa que si se mide un 0 en el primer qbit, el segundo qbit también tendrá un 0. Lo mismo ocurre para un valor de 1. Ambos qbits colapsarán al mismo estado.

La forma buena

Primero que nada, veamos el circuito cuántico; simplemente podemos imprimirlo (voy a eliminar casi todos los qbits e instrucciones porque el circuito cuántico es enorme):

>>> print(circuit)
       ┌───┐      ░                           ░ ┌───┐ ░ ┌─┐
  q_0: ┤ H ├──────░───■─────── ... ───────────░─┤ H ├─░─┤M├───── ... ───
       ├───┤      ░   │                       ░ ├───┤ ░ └╥┘┌─┐
  q_1: ┤ H ├──────░───┼─────── ... ───────────░─┤ H ├─░──╫─┤M├── ... ───
       ├───┤      ░   │                       ░ ├───┤ ░  ║ └╥┘

...

       ├───┤      ░   │    │         │    │   ░ ├───┤ ░  ║  ║        ┌─┐
q_231: ┤ H ├──────░───┼────┼── ... ──┼────┼───░─┤ H ├─░──╫──╫─── ... ┤M├
       ├───┤┌───┐ ░ ┌─┴─┐┌─┴─┐     ┌─┴─┐┌─┴─┐ ░ └───┘ ░  ║  ║        └╥┘
q_232: ┤ X ├┤ H ├─░─┤ X ├┤ X ├ ... ┤ X ├┤ X ├─░───────░──╫──╫─── ... ─╫─
       └───┘└───┘ ░ └───┘└───┘     └───┘└───┘ ░       ░  ║  ║         ║
c: 232/═══════════════════════ ... ══════════════════════╩══╩═══ ... ═╩═
                                                         0  1        231

El circuito cuántico parece abrumador, pero podemos enfocarnos únicamente en un qbit de la flag y en el último qbit (q_232). Debe haber una forma de saber si el qbit de la flag codifica un 0 o un 1 lógico observando las mediciones al simular el circuito.

En efecto, supongamos que estamos analizando un qbit que codifica un 1. Sea el estado inicial, donde tenemos dos qbits inicializados en , uno para el qbit de la flag y otro para el último qbit:

  • Estado inicial:

Ahora aplicamos la puerta Hadamard en el qbit de la flag y la puerta X en el último qbit:

  • Después de H y X:

A continuación, aplicamos la puerta Hadamard en el último qbit:

  • Después de H:

  • Ahora, hay una puerta CX, que hemos asumido al principio:

  • Finalmente, aplicamos una puerta Hadamard en el qbit de la flag:

Así que esta es la evolución de un qbit de la flag que codifica un 1 y del último qbit:

En caso de que el qbit de la flag codifique un 0, simplemente omitimos la puerta CX, por lo que el estado final es

Por lo tanto, esta es la evolución de un qbit de la flag que codifica un 0 y del último qbit:

Como se puede ver, el qbit de la flag termina en un estado si el bit de la flag es 0 y en un estado si el bit de la flag es 1, con un 100% de probabilidad. Por lo tanto, veremos estos resultados en las mediciones una vez que ejecutemos el circuito con todos los qbits inicializados en .

Podríamos haber inicializado los qbits en , o y obtener un resultado similar, pero vamos a mantener las cosas simples.

Para ejecutar el circuito, solo necesitamos usar las siguientes instrucciones:

>>> from qiskit_aer import AerSimulator
>>> 
>>> simulator = AerSimulator()
>>> result = simulator.run(circuit).result()

Ahora, podemos ver los resultados con get_counts:

>>> result.get_counts()
{'0100100001010100010000100111101101110100011010000011001101110010001100110101111100110001011100110101111101110011011101000011000101101100011011000101111101110011001100000110110100110011010111110110100000110000011100000011001101111101': 1024}

La cadena binaria anterior significa que el qbit q_231 colapsó a 0, el qbit q_230 colapsó a 1 y así sucesivamente hasta q_0 (no sé por qué aparece en orden inverso, pero se cancela con la función reversed inicial sobre los bits de la flag). Nótese que esta es la misma cadena binaria que obtuvimos anteriormente. Ahora, solo necesitamos tomar la cadena binaria anterior y convertirla a bytes.

Hay otra función que nos permite obtener la cadena binaria en formato hexadecimal, lo cual es más fácil de convertir a bytes:

>>> result.data()
{'counts': {'0x4854427b74683372335f31735f7374316c6c5f73306d335f683070337d': 1024}}

Flag

Y aquí está la flag:

>>> bytes.fromhex(list(result.data().get('counts').keys())[0][2:])
b'HTB{th3r3_1s_st1ll_s0m3_h0p3}'