Triangles

6 minutos de lectura

Se nos proporcionan los siguientes archivos fuente de Python:

triangulate.py:

import csv
import math
import random
from secret import getFlagLocation

arr = []
with open('grid.csv') as grid:
    for x in csv.reader(grid):
        arr.append(x)
        pass

def getDistance(x,y,x2,y2):
    return math.sqrt(math.pow(x - x2,2) + math.pow(y - y2,2))

def cap(num):
    if num > 99:
        return 99
    if num < 0:
        return 0
    return num

def createCoords(x,y):
    x1 = random.randint(-7,7)
    y1 = random.randint(-7,7)
    x2 = random.randint(-7,7)
    y2 = random.randint(-7,7)
    x3 = random.randint(-7,7)
    y3 = random.randint(-7,7)

    p1 = [cap(x1 + x), cap(y1 + y)]
    p2 = [cap(x2 + x), cap(y2 + y)]
    p3 = [cap(x3 + x), cap(y3 + y)]

    val1 = arr[p1[0]][p1[1]]
    val2 = arr[p2[0]][p2[1]]
    val3 = arr[p3[0]][p3[1]]

    distances = [(val1,getDistance(x,y,p1[0], p1[1])),(val2,getDistance(x,y,p2[0], p2[1])),(val3,getDistance(x,y,p3[0], p3[1])),(f"{val1}{val2}",getDistance(p1[0], p1[1],p2[0], p2[1])),(f"{val2}{val3}",getDistance(p2[0], p2[1],p3[0], p3[1])),(f"{val1}{val3}",getDistance(p1[0], p1[1],p3[0], p3[1]))]
    return distances

def createTriangulation():
    with open("out1.csv",'w') as out:
        writer = csv.writer(out)
        for coord in getFlagLocation():
            for val, dist in createCoords(coord[0],coord[1]):
                writer.writerow([val,dist])

def main():
    createTriangulation()

if __name__ == "__main__":
    main()

secret.py:

import csv

f = "HTB{fake_flag_for_testing}"

arr = []
with open('grid.csv') as grid:
    for x in csv.reader(grid):
        arr.append(x)
        pass

flagLocation = list()
# Coordinates are all placeholder values
flagLocation.append([1,2]) # H
flagLocation.append([2,2]) # T
flagLocation.append([3,2]) # B
flagLocation.append([4,2]) # {
flagLocation.append([55,2]) # f
flagLocation.append([65,2]) # a
flagLocation.append([75,2]) # k
flagLocation.append([85,2]) # e
flagLocation.append([9,25]) # _
flagLocation.append([5,2]) # f
flagLocation.append([6,2]) # l
flagLocation.append([7,2]) # a
flagLocation.append([8,2]) # g
flagLocation.append([9,2]) # _
flagLocation.append([1,12]) # f
flagLocation.append([2,22]) # o
flagLocation.append([3,32]) # r
flagLocation.append([4,12]) # _
flagLocation.append([5,22]) # t
flagLocation.append([6,32]) # e
flagLocation.append([7,22]) # s
flagLocation.append([8,42]) # t
flagLocation.append([9,52]) # i
flagLocation.append([12,2]) # n
flagLocation.append([11,2]) # g
flagLocation.append([13,2]) # }

def getFlagLocation():
    return flagLocation

def checkFlag():
    for i in range(len(f)):
        if arr[flagLocation[i][0]][flagLocation[i][1]] != f[i]:
            print("error")
            pass

Y también tenemos dos archivos CSV:

grid.csv:

P,1,<,:,M,A,T,b,3,*,V,T,C,E,c,:,$,Y,&,#,P,Y,8,#,f,*,y,T,e,^,C,J,I,I,e,e,r,Y,X,o,z,W,v,1,L,v,",",E,Z,A,Q,9,q,D,I,K,g,.,o,R,V,%,%,2,8,G,w,",",C,l,",",o,:,9,Z,#,T,B,",",W,t,q,c,n,p,2,G,A,6,{,R,v,L,q,j,m,T,:,V,3
u,g,^,R,*,;,>,s,y,D,o,V,J,r,@,I,3,},J,m,2,I,n,C,1,X,?,(,3,Y,o,k,g,W,3,:,8,k,u,m,i,0,m,c,h,b,O,3,3,},Y,.,],X,y,a,{,T,.,",",e,O,<,r,X,V,6,X,P,B,$,v,6,;,V,B,],w,(,*,f,T,*,>,2,",",R,U,x,z,>,5,.,f,&,1,3,3,F,I

...

},k,D,!,",",c,v,%,q,u,k,s,k,0,>,e,3,m,n,E,V,;,9,(,3,3,H,>,t,Y,&,k,b,S,l,^,i,[,0,*,m,R,%,P,D,^,*,0,t,Y,$,D,8,h,D,n,L,4,h,E,X,7,7,[,!,j,N,!,y,&,n,Q,.,5,u,W,&,I,A,X,.,[,q,6,f,K,M,k,[,&,3,d,),],8,},E,8,x,a

out.csv:

[,6.4031242374328485
p,5.0
4,2.23606797749979
[p,8.0
p4,2.8284271247461903
[4,6.324555320336759
X,7.211102550927978
1,7.211102550927978
5,7.0710678118654755
X1,8.0
15,11.045361017187261
X5,14.212670403551895

...

>,5.0
x,3.605551275463989
;,7.810249675906654
>x,7.0710678118654755
x;,4.242640687119285
>;,10.198039027185569

Análisis del código fuente

Como se puede ver, el archivo secret.py utiliza una cuadrícula 2D inicial (grid.csv) y asocia caracteres de la flag a coordenadas dentro de la cuadrícula. La flag mostrada en el archivo secret.py proporcionado es solo un ejemplo, para entender el propósito del script.

La función main en triangulate.py llama a createTriangulation:

def createTriangulation():
    with open("out1.csv",'w') as out:
        writer = csv.writer(out)
        for coord in getFlagLocation():
            for val, dist in createCoords(coord[0],coord[1]):
                writer.writerow([val,dist])

def main():
    createTriangulation()

Como se puede ver, por cada coordenada que proviene de getFlagLocation (de secret.py), se escriben algunas líneas en out.csv. Estas líneas provienen de createCoords:

def createCoords(x,y):
    x1 = random.randint(-7,7)
    y1 = random.randint(-7,7)
    x2 = random.randint(-7,7)
    y2 = random.randint(-7,7)
    x3 = random.randint(-7,7)
    y3 = random.randint(-7,7)

    p1 = [cap(x1 + x), cap(y1 + y)]
    p2 = [cap(x2 + x), cap(y2 + y)]
    p3 = [cap(x3 + x), cap(y3 + y)]

    val1 = arr[p1[0]][p1[1]]
    val2 = arr[p2[0]][p2[1]]
    val3 = arr[p3[0]][p3[1]]

    distances = [(val1,getDistance(x,y,p1[0], p1[1])),(val2,getDistance(x,y,p2[0], p2[1])),(val3,getDistance(x,y,p3[0], p3[1])),(f"{val1}{val2}",getDistance(p1[0], p1[1],p2[0], p2[1])),(f"{val2}{val3}",getDistance(p2[0], p2[1],p3[0], p3[1])),(f"{val1}{val3}",getDistance(p1[0], p1[1],p3[0], p3[1]))]
    return distances

En términos matemáticos, esta función recibe las coordenadas de un carácter de la flag como . Comienza generando tres puntos aleatorios: , , . Esos puntos se suman a las coordenadas de la flag:

Nótese que cap solo limita la cota superior e inferior dentro de la cuadrícula:

def cap(num):
    if num > 99:
        return 99
    if num < 0:
        return 0
    return num

A continuación, val1, val2 y val3 son los caracteres que aparecen en las coordenadas , y , respectivamente, en la cuadrícula.

La función retorna 6 tuplas:

val1 y
val2 y
val3 y
val1, val2 y
val2, val3 y
val1, val3 y

Donde representa la distancia euclídea:

def getDistance(x,y,x2,y2):
    return math.sqrt(math.pow(x - x2,2) + math.pow(y - y2,2))

En resumen, por cada carácter de la flag, se nos dan 6 líneas en la salida. Por ejemplo, para el primer carácter, tenemos:

[,6.4031242374328485
p,5.0
4,2.23606797749979
[p,8.0
p4,2.8284271247461903
[4,6.324555320336759

Solución

Nombramos algunos resultados:

Ahora, dibujamos un ejemplo:

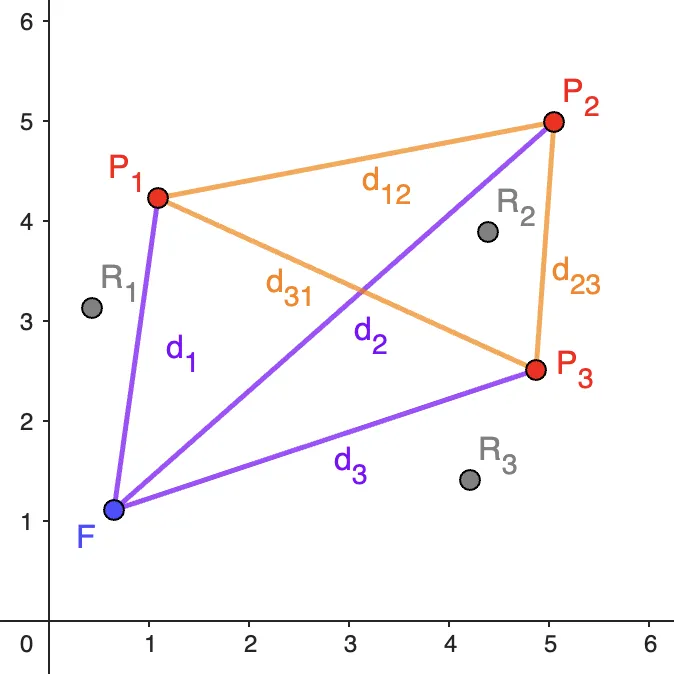
Triangles 1

Usando solo las distancias, no podemos ubicar las coordenadas del punto , necesitaremos los tres puntos , o . Si tuviéramos un solo punto , podemos asegurar que se encuentra en una circunferencia de radio y centro . Si también tenemos , sabemos que se encuentra en la intersección de las circunferencias de radios y y centros y , respectivamente. Sin embargo, hay dos intersecciones, por lo que necesitamos un tercer punto para asegurar un único punto donde ubicar .

Para encontrar los puntos , y adecuados, podemos probar varios puntos dentro de la cuadrícula y verificar si resultan en distancias , y . Nótese que se nos dan val1, val2 y val3, por lo que podemos tomar algunos candidatos para , y y probarlos.

Implementación

Comencemos escribiendo la solución en un script de Python. Primero, leemos los archivos CSV y definimos el diccionario de valores y las coordenadas que contienen esos valores:

#!/usr/bin/env python3

import csv

from collections import defaultdict
from itertools import product


with open('grid.csv') as f_grid, open('out.csv') as f_out:
    grid = [row for row in csv.reader(f_grid)]
    results = f_out.read().splitlines()

values = defaultdict(list)

for x, row in enumerate(grid):
    for y, value in enumerate(row):
        values[value].append(x + 1j * y)

Cuando se trabaja con coordenadas 2D en Python (y en Go), me gusta usar números complejos, porque es más fácil operar con ellos. Por ejemplo, la distancia euclídea entre dos puntos es simplemente el valor absoluto de la diferencia de dos números complejos:

Ahora, para cada secuencia de 6 líneas en out.csv (results), tomaremos val1, val2, val3 y las distancias , , , , y :

for i in range(0, len(results), 6):
    val1, d1 = results[i + 0][:1], float(results[i + 0][2:])
    val2, d2 = results[i + 1][:1], float(results[i + 1][2:])
    val3, d3 = results[i + 2][:1], float(results[i + 2][2:])

    d12 = float(results[i + 3][3:])
    d23 = float(results[i + 4][3:])
    d31 = float(results[i + 5][3:])

Primero, encontramos los puntos , y considerando todas las combinaciones de puntos que contienen val1, val2 y val3, y encontramos la que tiene las distancias , y :

    for P1, P2, P3 in product(values[val1], values[val2], values[val3]):
        if abs(P1 - P2) == d12 and abs(P2 - P3) == d23 and abs(P3 - P1) == d31:
            break

Una vez encontrados esos puntos, iteramos por todos los puntos de la cuadrícula (iterando el diccionario) e imprimimos el valor del punto que tiene distancias , y a los puntos , y , respectivamente:

    for value, points in values.items():
        for F in points:
            if abs(F - P1) == d1 and abs(F - P2) == d2 and abs(F - P3) == d3:
                print(value, end='')
                break

Flag

Si ejecutamos el script, obtendremos la flag:

$ python3 solve.py
HTB{sQU@r3s_R_4_N3rD$}

El script completo se puede encontrar aquí: solve.py.