<- CORCTF

two-wrongs

18 minutos de lectura

Se nos proporciona el código fuente en Python que cifra la flag:

from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile
from qiskit_aer import AerSimulator
import numpy as np
import random, os, binascii, sys
from Crypto.Cipher import AES
from flag import flag

key = os.urandom(16)
cipher = AES.new(key, AES.MODE_ECB)

sv_sim = AerSimulator(method="statevector")
bit_idxs = list(map(int, input('Select a sensor index to remove from each bit: ').split(' ')))

def enc_byte(b):
    sensor_vals = ''
    bit_encs = []
    for bit in format(b, '08b'):
        seed = int.from_bytes(os.urandom(8), sys.byteorder)
        sensor_val = enc_bit(bit, seed)
        sensor_vals += ''.join(sensor_val.split(' '))
        bit_encs.append((bit, seed))
    sensor_vals = list(sensor_vals)
    for i in range(8):
        sensor_vals[i * 6 + bit_idxs[i]] = '?'
    return ''.join(sensor_vals), bit_encs

def rand_bit_flip(qc, main, seed):
    if seed % 3 == 0:
        qc.x(main[seed % 7])
    elif seed % 3 == 1:
        qc.z(main[seed % 7])

def enc_bit(bit, seed):
    main = QuantumRegister(7)
    anc_x = QuantumRegister(3)
    anc_z = QuantumRegister(3)
    syn_x = ClassicalRegister(3)
    syn_z = ClassicalRegister(3)

    qc = QuantumCircuit(main, anc_x, anc_z, syn_x, syn_z)

    if bit == '1':
        qc.initialize([0, 1], main[6])

    for i in range(3):
        qc.h(main[i])

    qc.cx(main[6], main[3])
    qc.cx(main[6], main[4])

    for idx in [3,4,5]:
        qc.cx(main[0], main[idx])

    for idx in [3,5,6]:
        qc.cx(main[1], main[idx])

    for idx in [4,5,6]:
        qc.cx(main[2], main[idx])

    rand_bit_flip(qc, main, seed)

    qc.h(anc_x)
    qc.h(anc_z)


    norms = [[1, 0, 0, 1, 1, 1, 0],
             [0, 1, 0, 1, 0, 1, 1],
             [0, 0, 1, 0, 1, 1, 1]]

    for i in range(3):
        for j in range(len(norms[i])):
            if norms[i][j] == 1:
                qc.cx(anc_x[i], main[j])
                qc.cz(anc_z[i], main[j])

    qc.h(anc_x)
    qc.h(anc_z)
    qc.measure(anc_x, syn_x)
    qc.measure(anc_z, syn_z)

    cc = transpile(qc, sv_sim)
    result = sv_sim.run(cc).result()
    sv = [*result.get_counts()][0]
    return sv

def run_insts(qc, main, res, insts):
    for inst in insts:
        toks = inst.split(' ')
        if len(toks) < 2 or len(toks) > 3:
            continue
        arg1 = res if toks[1] == 'r' else main[int(toks[1])]
        if len(toks) == 3:
            arg2 = res if toks[2] == 'r' else main[int(toks[2])]
        if toks[0] == 'x':
            qc.x(arg1)
        elif toks[0] == 'y':
            qc.y(arg1)
        elif toks[0] == 'z':
            qc.z(arg1)
        elif toks[0] == 'h':
            qc.h(arg1)
        elif toks[0] == 'cx':
            qc.cx(arg1, arg2)
        elif toks[0] == 'cy':
            qc.cy(arg1, arg2)
        elif toks[0] == 'cz':
            qc.cz(arg1, arg2)
        else:
            exit()

def measure_bit(bit, seed, insts):
    main = QuantumRegister(7)
    res = QuantumRegister(1)
    ans = ClassicalRegister(1)
    anc_x = QuantumRegister(3)
    anc_z = QuantumRegister(3)
    syn_x = ClassicalRegister(3)
    syn_z = ClassicalRegister(3)

    qc = QuantumCircuit(main, res, ans, anc_x, anc_z, syn_x, syn_z)

    if bit == '1':
        qc.initialize([0, 1], main[6])

    for i in range(3):
        qc.h(main[i])

    qc.cx(main[6], main[3])
    qc.cx(main[6], main[4])

    for idx in [3,4,5]:
        qc.cx(main[0], main[idx])

    for idx in [3,5,6]:
        qc.cx(main[1], main[idx])

    for idx in [4,5,6]:
        qc.cx(main[2], main[idx])

    rand_bit_flip(qc, main, seed)

    qc.h(anc_x)
    qc.h(anc_z)

    norms = [[1, 0, 0, 1, 1, 1, 0],
             [0, 1, 0, 1, 0, 1, 1],
             [0, 0, 1, 0, 1, 1, 1]]

    for i in range(3):
        for j in range(len(norms[i])):
            if norms[i][j] == 1:
                qc.cx(anc_x[i], main[j])
                qc.cz(anc_z[i], main[j])

    qc.h(anc_x)
    qc.h(anc_z)
    qc.measure(anc_x, syn_x)
    qc.measure(anc_z, syn_z)

    run_insts(qc, main, res, insts)

    qc.measure(res, ans)

    cc = transpile(qc, sv_sim)
    result = sv_sim.run(cc).result()
    sv = [*result.get_counts()][0]
    return sv[-1]

print("Here's your flag:", binascii.hexlify(cipher.encrypt(flag.encode())))
print("Alright, good luck decoding.")
for b in key:
    sens, bits = enc_byte(b)
    print('Sensor measurements:', sens)
    insts = []
    print('Help me decode, one bit per line, instructions (ex. x 1, z 2) separated by semicolons:')  
    print('You can only touch main or res. Use an integer to index main, or r for res.')
    for _ in range(len(bits)):
        inst_set = input('').split(';')
        insts.append(inst_set)
    bit_ans = ''
    print(insts)
    for i in range(len(bits)):
        bit, seed = bits[i]
        bit_ans += measure_bit(bit, seed, insts[i])
    print('Your byte:', bit_ans)
    print('On to the next byte!')

El servidor del reto genera una clave de AES aleatoria de 16 bytes para cifrar la flag. Se nos da el texto cifrado, y luego el servidor usa un circuito cuántico para codificar cada bit de la clave de AES. Se nos permite obtener algunas medidas y agregar instrucciones al circuito después para que podamos intentar adivinar cada bit de la clave de AES.

Análisis del código fuente

Aquí está la flag cifrada:

# ...

from Crypto.Cipher import AES
from flag import flag

key = os.urandom(16)
cipher = AES.new(key, AES.MODE_ECB)

# ...

print("Here's your flag:", binascii.hexlify(cipher.encrypt(flag.encode())))  
print("Alright, good luck decoding.")

# ...

Luego, debemos ingresar algunos índices de mediciones que queremos “ocultar”:

sv_sim = AerSimulator(method="statevector")
bit_idxs = list(map(int, input('Select a sensor index to remove from each bit: ').split(' ')))  

def enc_byte(b):
    sensor_vals = ''
    bit_encs = []
    for bit in format(b, '08b'):
        seed = int.from_bytes(os.urandom(8), sys.byteorder)
        sensor_val = enc_bit(bit, seed)
        sensor_vals += ''.join(sensor_val.split(' '))
        bit_encs.append((bit, seed))
    sensor_vals = list(sensor_vals)
    for i in range(8):
        sensor_vals[i * 6 + bit_idxs[i]] = '?'
    return ''.join(sensor_vals), bit_encs

Durante los pasos iniciales de la resolución del reto, no entendí para qué era esto. Luego, me di cuenta de que cada byte de la clave de AES está codificado por separado, y luego cada uno de los 8 bits también está codificado por separado. La cuestión es que, en cada circuito cuántico, habrá 6 qbits que actúan como “sensores”, y el servidor medirá estos qbits. Sin embargo, se nos dice que ocultemos una de estas medidas.

Cada una de las 6 mediciones para cada bit se concatena a las siguientes 6 medidas del siguiente bit, y así sucesivamente. Después de eso, el servidor reemplazará los índices elegidos con un signo ?. Debido al formato de la salida de mediciones, fui más inteligente que el servidor y logré ocultar una sola medida para las 48 medidas ($6 \times 8$) mediante:

0 -6 -12 -18 -24 -30 -36 -42

El payload anterior engaña al bucle for para sobrescribir siempre la primera medición por un signo ?.

Además, el servidor calculará una semilla aleatoria y la usará para codificar el bit en el circuito cuántico. Entonces, recibiremos las medidas de los sensores.

Codificación de bits

Para cada bit, se genera un nuevo circuito cuántico con esta función:

def enc_bit(bit, seed):
    main = QuantumRegister(7)
    anc_x = QuantumRegister(3)
    anc_z = QuantumRegister(3)
    syn_x = ClassicalRegister(3)
    syn_z = ClassicalRegister(3)

    qc = QuantumCircuit(main, anc_x, anc_z, syn_x, syn_z)  

    if bit == '1':
        qc.initialize([0, 1], main[6])

    for i in range(3):
        qc.h(main[i])

    qc.cx(main[6], main[3])
    qc.cx(main[6], main[4])

    for idx in [3,4,5]:
        qc.cx(main[0], main[idx])

    for idx in [3,5,6]:
        qc.cx(main[1], main[idx])

    for idx in [4,5,6]:
        qc.cx(main[2], main[idx])

    rand_bit_flip(qc, main, seed)

    qc.h(anc_x)
    qc.h(anc_z)


    norms = [[1, 0, 0, 1, 1, 1, 0],
             [0, 1, 0, 1, 0, 1, 1],
             [0, 0, 1, 0, 1, 1, 1]]

    for i in range(3):
        for j in range(len(norms[i])):
            if norms[i][j] == 1:
                qc.cx(anc_x[i], main[j])
                qc.cz(anc_z[i], main[j])

    qc.h(anc_x)
    qc.h(anc_z)
    qc.measure(anc_x, syn_x)
    qc.measure(anc_z, syn_z)

    cc = transpile(qc, sv_sim)
    result = sv_sim.run(cc).result()
    sv = [*result.get_counts()][0]
    return sv

Parece aterrador, ¡y lo es! En resumen, tenemos un circuito cuántico con 7 qbits llamados main, luego 3 qbits nombrados anc_x y 3 qbits llamados anc_z. También hay registros clásicos para almacenar las medidas de anc_x y anc_z.

Lo único que cambia entre codificar un bit 0 o un bit 1 es que el qbit main[6] se inicializa en $\ket{0}$ o en $\ket{1}$, respectivamente.

El circuito comprende muchas puertas cuánticas, principalmente puertas de Hadamard, X-controlada y Z-controlads entre los qbits de main. Después de eso, se produce un bit-flip aleatorio, que depende de la semilla:

def rand_bit_flip(qc, main, seed):  
    if seed % 3 == 0:
        qc.x(main[seed % 7])
    elif seed % 3 == 1:
        qc.z(main[seed % 7])

Esta función agrega una puerta X o una puerta Z a uno de los qbits de main. Como se puede ver, hay 21 casos posibles ($3 \times 7$), aunque 7 de ellos (seed % 3 == 2) son equivalentes (no hay bit-flip).

Después del bit-flip, se aplican algunas puertas entre anc_x, anc_z y main. El servidor mide anc_z y anc_z y genera los resultados como una cadena de 6 bits. Una vez que se completan los 8 bits de un byte, recibimos la cadena de 48 bits de las mediciones (con signos ? en las ocultas):

for b in key:
    sens, bits = enc_byte(b)
    print('Sensor measurements:', sens)
    insts = []
    print('Help me decode, one bit per line, instructions (ex. x 1, z 2) separated by semicolons:')  
    print('You can only touch main or res. Use an integer to index main, or r for res.')
    for _ in range(len(bits)):
        inst_set = input('').split(';')
        insts.append(inst_set)
    bit_ans = ''
    print(insts)
    for i in range(len(bits)):
        bit, seed = bits[i]
        bit_ans += measure_bit(bit, seed, insts[i])
    print('Your byte:', bit_ans)
    print('On to the next byte!')

A continuación, se nos permite agregar más puertas al circuito y tener una medición adicional, utilizando measure_bit:

def measure_bit(bit, seed, insts):
    main = QuantumRegister(7)
    res = QuantumRegister(1)
    ans = ClassicalRegister(1)
    anc_x = QuantumRegister(3)
    anc_z = QuantumRegister(3)
    syn_x = ClassicalRegister(3)
    syn_z = ClassicalRegister(3)

    qc = QuantumCircuit(main, res, ans, anc_x, anc_z, syn_x, syn_z)  

    if bit == '1':
        qc.initialize([0, 1], main[6])

    for i in range(3):
        qc.h(main[i])

    qc.cx(main[6], main[3])
    qc.cx(main[6], main[4])

    for idx in [3,4,5]:
        qc.cx(main[0], main[idx])

    for idx in [3,5,6]:
        qc.cx(main[1], main[idx])

    for idx in [4,5,6]:
        qc.cx(main[2], main[idx])

    rand_bit_flip(qc, main, seed)

    qc.h(anc_x)
    qc.h(anc_z)

    norms = [[1, 0, 0, 1, 1, 1, 0],
             [0, 1, 0, 1, 0, 1, 1],
             [0, 0, 1, 0, 1, 1, 1]]

    for i in range(3):
        for j in range(len(norms[i])):
            if norms[i][j] == 1:
                qc.cx(anc_x[i], main[j])
                qc.cz(anc_z[i], main[j])

    qc.h(anc_x)
    qc.h(anc_z)
    qc.measure(anc_x, syn_x)
    qc.measure(anc_z, syn_z)

    run_insts(qc, main, res, insts)

    qc.measure(res, ans)

    cc = transpile(qc, sv_sim)
    result = sv_sim.run(cc).result()
    sv = [*result.get_counts()][0]
    return sv[-1]

Esta función genera el mismo circuito cuántico que enc_bit, pero usando un qbit res adicional y un registro clásico para medir dicho qbit al final. El circuito se inicializa como antes y usa la misma semilla para rand_bit_flip. Además, se realizan las mismas 6 mediciones en anc_x y anc_z. Está aquí donde se nos permite agregar puertas cuánticas entre los qbits main y res antes de medir el qbit res.

Las puertas que podemos usar son estas:

  • Puertas de Pauli (X, Y, Z)
  • Puertas controladas (CX, CY, CZ)
  • Puerta de Hadamard (H)
def run_insts(qc, main, res, insts):
    for inst in insts:
        toks = inst.split(' ')
        if len(toks) < 2 or len(toks) > 3:
            continue
        arg1 = res if toks[1] == 'r' else main[int(toks[1])]
        if len(toks) == 3:
            arg2 = res if toks[2] == 'r' else main[int(toks[2])]  
        if toks[0] == 'x':
            qc.x(arg1)
        elif toks[0] == 'y':
            qc.y(arg1)
        elif toks[0] == 'z':
            qc.z(arg1)
        elif toks[0] == 'h':
            qc.h(arg1)
        elif toks[0] == 'cx':
            qc.cx(arg1, arg2)
        elif toks[0] == 'cy':
            qc.cy(arg1, arg2)
        elif toks[0] == 'cz':
            qc.cz(arg1, arg2)
        else:
            exit()

Entonces, con todo esto, debemos encontrar una manera de determinar si el circuito cuántico se inicializó con main[6] puesto a $\ket{0}$ o a $\ket{1}$ Para obtener los bits de la tecla AES.

Contexto

Este reto necesita ciertos conocimientos sobre computación cuántica. Probablemente, todavía no esté preparado para escribir sobre estos conceptos cuánticos de manera rigurosa aquí, pero puedo enumerar algunos recursos que me parecieron buenos para comprender estos conceptos:

Intentaré expresar algunos conceptos clave en caso de que no desee sumergirse en los enlaces anteriores:

  • En computación cuántica, los qbit no tienen un valor concreto, tienen un estado de superposición. Esto significa que pueden tener cualquier valor, hasta que se mida el qbit. Una vez que se observa un qbit, colapsa a un valor (0 o 1) y no se puede cambiar. Y esto sucede con cierta probabilidad, que puede expresarse como $\ket{\psi} = \alpha \cdot \ket{0} + \beta \cdot \ket{1}$, donde $|\alpha|^2$ y $|\beta|^2$ representar la probabilidad de colapsar a 0 o a 1, por lo que $|\alpha|^2 + |\beta|^2 = 1$

  • Una puerta de Hadamard (H) produce un “cambio de base”:

    • $H \ket{0} = \displaystyle\frac{1}{\sqrt{2}} \big(\ket{0} + \ket{1}\big) \equiv \ket{+}$

    • $H \ket{1} = \displaystyle\frac{1}{\sqrt{2}} \big(\ket{0} - \ket{1}\big) \equiv \ket{-}$

  • Medir un qbit que ha sido transformado por una puerta de Hadamard tiene un 50% de posibilidades de colapsar a 0 y a 1

  • Las puertas de Pauli (X, Y, Z) se comportan de la siguiente manera:

    • $X \ket{\psi} = X(\alpha \cdot \ket{0} + \beta \cdot \ket{1}) = \beta \cdot \ket{0} + \alpha \cdot \ket{1}$

    • $Y \ket{\psi} = Y(\alpha \cdot \ket{0} + \beta \cdot \ket{1}) = - \mathrm{i} \cdot \beta \cdot \ket{0} + \mathrm{i} \cdot \alpha \cdot \ket{1}$

    • $Z \ket{\psi} = Z(\alpha \cdot \ket{0} + \beta \cdot \ket{1}) = \alpha \cdot \ket{0} - \beta \cdot \ket{1}$

  • Las puertas controladas (CX, CY, CZ) implican dos qbits: el qbit de control y el qbit objetivo. Si el qbit de control es $\ket{1}$ la operación (X, Y o Z) se realiza en el qbit objetivo.

  • Una aplicación directa de la puerta CX (también conocida como CNOT) es el estado de Bell, que es una forma de entrelazamiento cuántico:

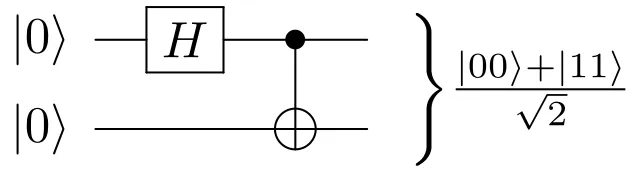
two-wrongs 1

El circuito anterior tiene 3 estados diferentes:

  • Estado inicial: $\ket{0} \otimes \ket{0} \equiv \ket{00}$

  • Después de la puerta H: $(H \ket{0}) \otimes \ket{0} = \left(\displaystyle\frac{\ket{0} + \ket{1}}{\sqrt{2}} \right) \otimes \ket{0} = \displaystyle\frac{\ket{00} + \ket{10}}{\sqrt{2}}$

  • Después de la puerta CNOT: $\mathrm{CNOT} \left(\displaystyle\frac{\ket{00} + \ket{10}}{\sqrt{2}}\right) = \displaystyle\frac{\ket{00} + \ket{11}}{\sqrt{2}} \equiv \ket{\Phi^+}$

En este punto, ambos qbits están entrelazados, lo que significa que si medimos un 0 en el primer qbit, el segundo qbit tendrá un 0 también, y viceversa. Lo mismo sucede para un valor de 1. Ambos qbits colapsarán al mismo estado.

Solución

Al final, mi solución no requería mucho conocimiento sobre computación cuántica. En cambio, lo que hice fue encontrar patrones probando dinámicamente el circuito dado.

De hecho los circuitos generados por enc_bit y measure_bit son muy complejos para analizarlos a mano. Este es un ejemplo para un circuito que codifica un bit 1 con una semilla que es 15 módulo $3 \times 7$:

               ┌───┐                                          ┌───┐
q254_0: ───────┤ H ├──────────────■────■─────────■────────────┤ X ├───────────■────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────  
               ├───┤              │    │         │            └─┬─┘     ┌───┐ │                           ┌───┐                                                           ┌───┐
q254_1: ───────┤ H ├──────────────┼────┼────■────┼─────────■────┼────■──┤ X ├─┼───────────────────────────┤ X ├─────────■─────────────────────────────────────────────────┤ X ├────────────────────────────────
               ├───┤              │    │    │    │         │    │    │  └───┘ │                           └─┬─┘┌───┐    │                                                 └─┬─┘                ┌───┐
q254_2: ───────┤ H ├──────────────┼────┼────┼────┼────■────┼────┼────┼────■───┼────────■────────────────────┼──┤ X ├────┼───────■───────────────────────────────────────────┼──────────────────┤ X ├───────────
               └───┘       ┌───┐┌─┴─┐  │  ┌─┴─┐  │    │    │    │    │    │   │ ┌───┐  │                    │  └─┬─┘    │ ┌───┐ │                                           │                  └─┬─┘
q254_3: ───────────────────┤ X ├┤ X ├──┼──┤ X ├──┼────┼────┼────┼────┼────┼───┼─┤ X ├──┼───■────────────────┼────┼──────┼─┤ X ├─┼────────────■──────────────────────────────┼────────────────────┼─────────────
                           └─┬─┘├───┤┌─┴─┐└───┘  │  ┌─┴─┐  │    │    │    │   │ └─┬─┘  │   │ ┌───┐          │    │      │ └─┬─┘ │ ┌───┐      │                              │                    │
q254_4: ─────────────────────┼──┤ X ├┤ X ├───────┼──┤ X ├──┼────┼────┼────┼───┼───┼────┼───┼─┤ X ├─■────────┼────┼──────┼───┼───┼─┤ X ├──────┼───────■──────────────────────┼────────────────────┼─────────────
                             │  └─┬─┘└───┘     ┌─┴─┐└───┘┌─┴─┐  │    │  ┌─┴─┐ │   │    │   │ └─┬─┘ │ ┌───┐  │    │      │   │   │ └─┬─┘      │ ┌───┐ │               ┌───┐  │                    │
q254_5: ─────────────────────┼────┼────────────┤ X ├─────┤ X ├──┼────┼──┤ X ├─┼───┼────┼───┼───┼───┼─┤ X ├──┼────┼───■──┼───┼───┼───┼────────┼─┤ X ├─┼─────■─────────┤ X ├──┼───■────────────────┼─────────────
        ┌─────────────────┐  │    │            └───┘     └───┘  │  ┌─┴─┐└───┘ │   │  ┌─┴─┐ │   │   │ └─┬─┘  │    │   │  │   │   │   │        │ └─┬─┘ │     │ ┌───┐   └─┬─┘  │   │ ┌───┐          │
q254_6: ┤ Initialize(0,1) ├──■────■─────────────────────────────┼──┤ X ├──────┼───┼──┤ X ├─┼───┼───┼───┼────┼────┼───┼──┼───┼───┼───┼────────┼───┼───┼─────┼─┤ X ├─■───┼────┼───┼─┤ X ├──────■───┼─────────────
        └──────┬───┬──────┘                                     │  └───┘      │   │  └───┘ │   │   │   │    │    │   │  │   │   │   │  ┌───┐ │   │   │ ┌─┐ │ └─┬─┘ │   │    │   │ └─┬─┘      │   │
q255_0: ───────┤ H ├────────────────────────────────────────────■─────────────┼───■────────┼───■───┼───■────┼────┼───┼──┼───┼───┼───┼──┤ H ├─┼───┼───┼─┤M├─┼───┼───┼───┼────┼───┼───┼────────┼───┼─────────────
               ├───┤                                                          │            │       │        │    │   │  │   │   │   │  └───┘ │   │   │ └╥┘ │   │   │   │    │   │   │  ┌───┐ │   │  ┌─┐
q255_1: ───────┤ H ├──────────────────────────────────────────────────────────┼────────────┼───────┼────────■────┼───┼──┼───■───┼───┼────────┼───■───┼──╫──┼───■───┼───┼────■───┼───┼──┤ H ├─┼───┼──┤M├────────
               ├───┤                                                          │            │       │             │   │  │       │   │        │       │  ║  │       │   │        │   │  └───┘ │   │  └╥┘┌───┐┌─┐
q255_2: ───────┤ H ├──────────────────────────────────────────────────────────┼────────────┼───────┼─────────────■───┼──┼───────┼───■────────┼───────┼──╫──┼───────┼───■────────┼───■────────┼───■───╫─┤ H ├┤M├
               ├───┤                                                          │            │       │                 │  │ ┌───┐ │  ┌─┐       │       │  ║  │       │            │            │       ║ └───┘└╥┘
q256_0: ───────┤ H ├──────────────────────────────────────────────────────────■────────────■───────■─────────────────■──┼─┤ H ├─┼──┤M├───────┼───────┼──╫──┼───────┼────────────┼────────────┼───────╫───────╫─
               ├───┤                                                                                                    │ └───┘ │  └╥┘       │       │  ║  │       │ ┌───┐ ┌─┐  │            │       ║       ║
q256_1: ───────┤ H ├────────────────────────────────────────────────────────────────────────────────────────────────────■───────┼───╫────────■───────┼──╫──■───────■─┤ H ├─┤M├──┼────────────┼───────╫───────╫─
               ├───┤                                                                                                            │   ║                │  ║            └───┘ └╥┘  │            │ ┌───┐ ║  ┌─┐  ║
q256_2: ───────┤ H ├────────────────────────────────────────────────────────────────────────────────────────────────────────────■───╫────────────────■──╫───────────────────╫───■────────────■─┤ H ├─╫──┤M├──╫─
               └───┘                                                                                                                ║                   ║                   ║                  └───┘ ║  └╥┘  ║
 c62: 3/════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╬═══════════════════╩═══════════════════╬════════════════════════╩═══╬═══╩═
                                                                                                                                    ║                   0                   ║                        1   ║   2
 c63: 3/════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╩═══════════════════════════════════════╩════════════════════════════╩═════
                                                                                                                                    0                                       1                            2

En realidad, este es un circuito de corrección de errores cuánticos, pero no es tan relevante para resolver el reto.

Entonces, recordemos que hay 21 semillas posibles (estamos considerando módulo $3 \times 7$), aunque 7 de ellas son equivalentes. Luego, tenemos un bit 0 o un bit 1. Eso nos da 42 casos. Usé el siguiente código para obtener estas ideas:

for seed in range(21):
    for bit in range(2):
        print(f'{bit = }; {seed = :2d}; enc = {enc_bit(str(bit), seed)}')  

$ python3 test.py
bit = 0; seed =  0; enc = 001 000  
bit = 1; seed =  0; enc = 001 000
bit = 0; seed =  1; enc = 000 010
bit = 1; seed =  1; enc = 000 010
bit = 0; seed =  2; enc = 000 000
bit = 1; seed =  2; enc = 000 000
bit = 0; seed =  3; enc = 011 000
bit = 1; seed =  3; enc = 011 000
bit = 0; seed =  4; enc = 000 101
bit = 1; seed =  4; enc = 000 101
bit = 0; seed =  5; enc = 000 000
bit = 1; seed =  5; enc = 000 000
bit = 0; seed =  6; enc = 110 000
bit = 1; seed =  6; enc = 110 000
bit = 0; seed =  7; enc = 000 001
bit = 1; seed =  7; enc = 000 001
bit = 0; seed =  8; enc = 000 000
bit = 1; seed =  8; enc = 000 000
bit = 0; seed =  9; enc = 100 000
bit = 1; seed =  9; enc = 100 000
bit = 0; seed = 10; enc = 000 011
bit = 1; seed = 10; enc = 000 011
bit = 0; seed = 11; enc = 000 000
bit = 1; seed = 11; enc = 000 000
bit = 0; seed = 12; enc = 111 000
bit = 1; seed = 12; enc = 111 000
bit = 0; seed = 13; enc = 000 110
bit = 1; seed = 13; enc = 000 110
bit = 0; seed = 14; enc = 000 000
bit = 1; seed = 14; enc = 000 000
bit = 0; seed = 15; enc = 010 000
bit = 1; seed = 15; enc = 010 000
bit = 0; seed = 16; enc = 000 100
bit = 1; seed = 16; enc = 000 100
bit = 0; seed = 17; enc = 000 000
bit = 1; seed = 17; enc = 000 000
bit = 0; seed = 18; enc = 101 000
bit = 1; seed = 18; enc = 101 000
bit = 0; seed = 19; enc = 000 111
bit = 1; seed = 19; enc = 000 111
bit = 0; seed = 20; enc = 000 000
bit = 1; seed = 20; enc = 000 000

Como se puede ver, la salida de enc_bit es siempre la misma para cada semilla, sin importar el bit codificado. Además, hay que tener en cuenta que no hay dos salidas iguales (excepto para seed % 3 == 2). Como resultado, si se nos da una cadena de mediciones de 6 bits, podemos saber directamente qué semilla se usó para rand_bit_flip.

Recordemos que en cada byte, ocultaremos una medición (la primera). Esto significa que tendremos un 50% de posibilidades de adivinar el primer bit correctamente. Como la clave de AES está compuesta por 16 bytes, terminaremos la solución con una fuerza bruta de 16 bits.

Ahora, debemos saber si la inicialización de main[6] fue $\ket{0}$ o $\ket{1}$. Para esto, podemos usar el sentido común. ¿Qué pasa si “deshacemos” las operaciones del circuito? Sorprendentemente, funcionó.

Observe que el anc_x y anc_z ya se midieron, por lo que no los necesitaremos en absoluto. El enfoque a seguir es aplicar las puertas cuánticas inversas en orden inverso. Esta vez, las puertas inversas son las propias puertas (es decir, el inverso de CX es CX, el inverso de H es H…). Además, debemos agregar la puerta adicional de rand_bit_flip, ya que conocemos la semilla.

Finalmente, agregaremos una puerta CX entre main[6] (control) y res (objetivo), de manera que si main[6] se decodifica como $\ket{0}$, tendremos un $\ket{0}$ en res; y si main[6] se decodifica como $\ket{1}$, actuará en res para tener también $\ket{1}$.

Implementación

En primer lugar, nos conectamos al reto, tomamos la flag cifrada y establecemos las medidas ocultas (con el truco anterior):

io = get_process()

io.sendlineafter(b'Select a sensor index to remove from each bit: ', b'0 -6 -12 -18 -24 -30 -36 -42')  
io.recvuntil(b"Here's your flag: b'")
enc_flag = bytes.fromhex(io.recvuntilS(b"'", drop=True))

Luego, definimos el mapeo entre salidas de medición y puertas adicionales de rand_bit_flip, usando el formato de run_insts (para 000000, no hay puerta adicional). También definimos la lista de puertas en orden inverso, con el CX final entre main[6] y res:

rands = {
    '000000': [],
    '001000': ['x 0'],  
    '000010': ['z 1'],
    '011000': ['x 3'],
    '000101': ['z 4'],
    '110000': ['x 6'],
    '000001': ['z 0'],
    '100000': ['x 2'],
    '000011': ['z 3'],
    '111000': ['x 5'],
    '000110': ['z 6'],
    '010000': ['x 1'],
    '000100': ['z 2'],
    '101000': ['x 4'],
    '000111': ['z 5'],
}

rev_insts = [
    'cx 2 6',
    'cx 2 5',
    'cx 2 4',
    'cx 1 6',
    'cx 1 5',
    'cx 1 3',
    'cx 0 5',
    'cx 0 4',
    'cx 0 3',
    'cx 6 4',
    'cx 6 3',
    'h 2',
    'h 1',
    'h 0',
    'cx 6 r',
]

A continuación, para cada medición de cada uno de los 8 bits, creamos la lista de instrucciones y recibimos la medición de res, que debería ser el estado de main[6]:

key = bytearray()
prog = io.progress('Bytes')

for b in range(16):
    prog.status(f'{b + 1} / 16')
    io.recvuntil(b'Sensor measurements: ')
    all_sensors = io.recvlineS().strip().replace('?', '0')
    sensors = [all_sensors[i : i + 6] for i in range(0, 8 * 6, 6)]
    io.recvuntil(b'You can only touch main or res. Use an integer to index main, or r for res.\n')  

    for i in range(8):
        insts = ';'.join(rands[sensors[i]] + rev_insts).encode()
        io.sendline(insts)

    io.recvuntil(b'Your byte: ')
    key.append(int(io.recvlineS(), 2))

prog.success(f'16 / 16')
io.info(f'Almost {key = }')

Finalmente, aplicamos una fuerza bruta de 16 bits sobre el bit más significativo de cada byte de la clave de AES hasta que obtengamos la flag:

for p in product(range(2), repeat=16):
    for i, b in enumerate(p):
        key[i] = (b << 7) | (key[i] & 0x7f)

    if b'corctf{' in (flag := AES.new(key, AES.MODE_ECB).decrypt(enc_flag)):  
        io.success(f'{key = }')
        io.success(f'Flag: {flag.decode()}')
        break

Flag

Si ejecutamos el script, encontraremos la flag:

$ python3 solve.py be.ax 32422
[+] Opening connection to be.ax on port 32422: Done
[+] Starting local process '/usr/bin/bash': pid 358568
[*] Stopped process '/usr/bin/bash' (pid 358568)
[+] Bytes: 16 / 16
[*] Almost key = bytearray(b'5\xc8(f\xe4U\x88v\xd25\xc9\xa1F\xc6\xc8\x8c')  
[+] key = bytearray(b'5\xc8(\xe6\xe4U\x88v\xd25\xc9\xa1F\xc6\xc8\x8c')
[+] Flag: corctf{c0rr3ct_CORr3Ct!nG_9aenq}
[*] Closed connection to be.ax port 32422

El script completo se puede encontrar aquí: solve.py.