winter
5 minutos de lectura
Se nos proporciona el código fuente en Python de un servidor:
#!/usr/local/bin/python
import os
from hashlib import sha256
class Wots:
def __init__(self, sk, vk):
self.sk = sk
self.vk = vk
@classmethod
def keygen(cls):
sk = [os.urandom(32) for _ in range(32)]
vk = [cls.hash(x, 256) for x in sk]
return cls(sk, vk)
@classmethod
def hash(cls, x, n):
for _ in range(n):
x = sha256(x).digest()
return x
def sign(self, msg):
m = self.hash(msg, 1)
sig = b''.join([self.hash(x, 256 - n) for x, n in zip(self.sk, m)])
return sig
def verify(self, msg, sig):
chunks = [sig[i:i+32] for i in range(0, len(sig), 32)]
m = self.hash(msg, 1)
vk = [self.hash(x, n) for x, n in zip(chunks, m)]
return self.vk == vk
if __name__ == '__main__':
with open('flag.txt') as f:
flag = f.read().strip()
wots = Wots.keygen()
msg1 = bytes.fromhex(input('give me a message (hex): '))
sig1 = wots.sign(msg1)
assert wots.verify(msg1, sig1)
print('here is the signature (hex):', sig1.hex())
msg2 = bytes.fromhex(input('give me a new message (hex): '))
if msg1 == msg2:
print('cheater!')
exit()
sig2 = bytes.fromhex(input('give me the signature (hex): '))
if wots.verify(msg2, sig2):
print(flag)
else:
print('nope')
Análisis del código fuente
El servidor implementa Winternitz One-Time Signature (WOTS), que es un algoritmo de firma asimétrico basado en funciones hash. El propósito de este reto es decirle al servidor que firme un mensaje y luego falsificar una firma para un mensaje diferente:
if __name__ == '__main__':
with open('flag.txt') as f:
flag = f.read().strip()
wots = Wots.keygen()
msg1 = bytes.fromhex(input('give me a message (hex): '))
sig1 = wots.sign(msg1)
assert wots.verify(msg1, sig1)
print('here is the signature (hex):', sig1.hex())
msg2 = bytes.fromhex(input('give me a new message (hex): '))
if msg1 == msg2:
print('cheater!')
exit()
sig2 = bytes.fromhex(input('give me the signature (hex): '))
if wots.verify(msg2, sig2):
print(flag)
else:
print('nope')
El algoritmo WOTS en sí está bien implementado. El problema aquí es que se usa de forma errónea, ya que es “one-time”, por lo que no es seguro usar la misma clave privada para firmar dos mensajes diferentes.
WOTS
Revisemos cómo funciona WOTS:
- La clave privada está compuesta por 32 valores, cada uno de ellos se compone de 32 bytes aleatorios. Llamemos a la clave privada
- La clave pública se deriva de la clave privada utilizando una función de hash SHA256 iterada, denotada por
. Entonces, cada para
Nótese que
Podemos representar la relación entre clave privada y pública de la siguiente manera:
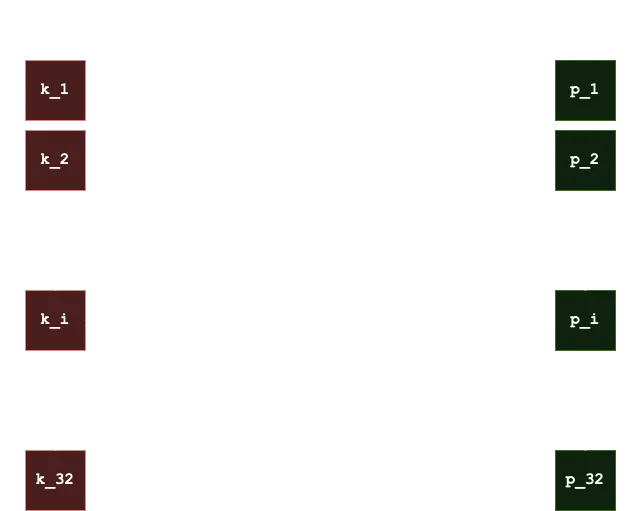
Ahora, para firmar un mensaje, se toma el hash SHA256 del mensaje como 32 bytes (
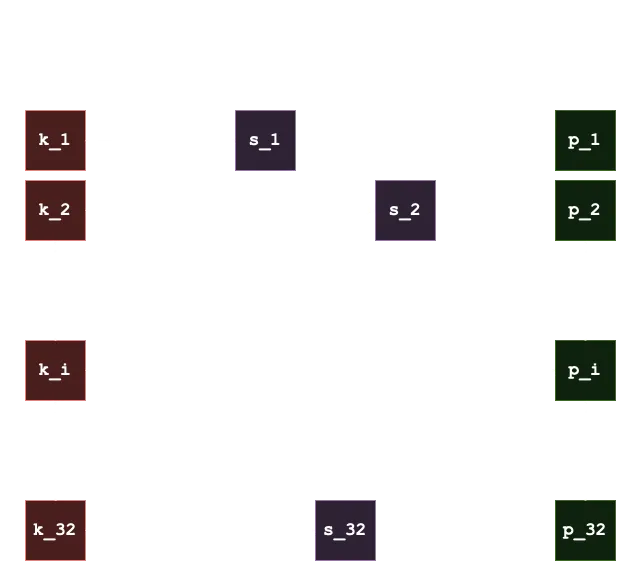
Luego, para verificar que un mensaje tiene una firma dada, tomamos el hash SHA256 del mensaje como 32 bytes (
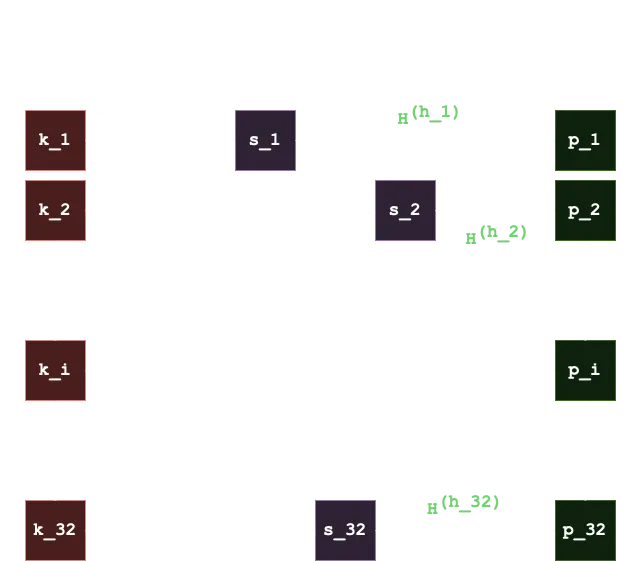
Explotación
La idea aquí es que, si tenemos dos mensajes cuyos hashes SHA256 cumplen que todos los bytes del primer hash son más grandes que todos los bytes del segundo hash (elemento a elemento), entonces podemos hallar la firma para el segundo mensaje a partir de la primera firma:
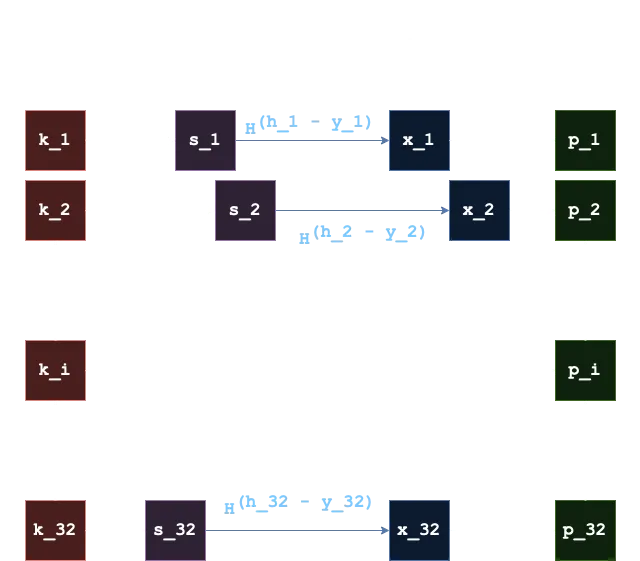
Si encontramos tales mensajes, podremos falsificar una firma aplicando la función hash un número de veces igual a la diferencia entre los bytes de cada hash.
Implementación
En lugar de probar dos mensajes aleatorias y ver si todos los bytes de sus hashes son más grandes que los demás, decidí usar otro enfoque. Generé mensajes aleatorios hasta que encontré uno cuyos bytes de hash son todos mayores que 0x80. Luego, busqué otro mensaje cuyos bytes de hash son todos menores que 0x80. Como resultado, tengo un mensaje cuyos bytes de hash son todos mayores que los bytes de hash del otro mensaje:
$ python3 -q
>>> from hashlib import sha256
>>> import os
>>>
>>> while True:
... msg = os.urandom(32)
... h = sha256(msg).digest()
... if all(hh >= 0x80 for hh in h):
... break
>>> msg
b'\xa8\xf1\x16\xa4\xf6#sH|\xa4\xbbV\xc5\x08\xeaY\x1b\xc8\x0f\x9bbC:\x19\x0c\xd8i\x1d*\xa7M)'
>>>
>>>
>>> while True:
... msg = os.urandom(32)
... h = sha256(msg).digest()
... if all(hh < 0x80 for hh in h):
... break
>>> msg
b'C:\xe5\xf71\xec\xf7![n/\xaa\xed6\xbb\xdd\x14\xc8\xd6E\xb7\xc0\n}9\x19\x13\xd3g\x1a\x86\xc3'
Con ambos mensajes, podemos firmar el primero (todos los bytes de hash más grandes que 0x80) y usar esa firma para hallar la firma del segundo mensaje:
def sha256_n(msg, n):
for _ in range(n):
msg = sha256(msg).digest()
return msg
msg1 = b'\xa8\xf1\x16\xa4\xf6#sH|\xa4\xbbV\xc5\x08\xeaY\x1b\xc8\x0f\x9bbC:\x19\x0c\xd8i\x1d*\xa7M)'
msg2 = b'C:\xe5\xf71\xec\xf7![n/\xaa\xed6\xbb\xdd\x14\xc8\xd6E\xb7\xc0\n}9\x19\x13\xd3g\x1a\x86\xc3'
h1, h2 = sha256_n(msg1, 1), sha256_n(msg2, 1)
assert all(a > b for a, b in zip(h1, h2))
io = get_process()
io.sendlineafter(b'give me a message (hex): ', msg1.hex().encode())
io.recvuntil(b'here is the signature (hex): ')
sig1 = bytes.fromhex(io.recvline().decode())
sig2 = b''
for i in range(0, len(sig1), 32):
sig2 += sha256_n(sig1[i: i + 32], h1[i // 32] - h2[i // 32])
io.sendlineafter(b'give me a new message (hex): ', msg2.hex().encode())
io.sendlineafter(b'give me the signature (hex): ', sig2.hex().encode())
io.success(io.recvline().decode())
Flag
Con esto, podemos conectarnos a la instancia remota y obtener la flag:
$ python3 solve.py mc.ax 31001
[+] Opening connection to mc.ax on port 31001: Done
[+] dice{according_to_geeksforgeeks}
[*] Closed connection to mc.ax port 31001
El script completo se puede encontrar aquí: solve.py.