<- HACKON CTF

El Reset de 1745

16 minutos de lectura

Se nos proporciona un script en Python que crea una clave privada de RSA y nos da algo de información adicional:

from Crypto.PublicKey import RSA
from Crypto.Util.number import getPrime,inverse
from sage.all import cos,floor,sqrt


def main():
    p = getPrime(1024)
    q = getPrime(1024)
    N = p*q
    print(N,q >> 450)
    print(cos(q >> 450).n(4096))
    # -0.83677025469083783941541701752761854754793836436580928644247008941810266469532458996045447348443859400152817824525738732652478723578550322419681449352934903962868272432839950443728133311767399079690030001079242722034971856216464693298008475334803612328029119715730610948114017183466860376219520135065944451843458471230390067711216822465611823803314088335568327990572989813880317949003496128817743756941657517592732976171161188449564836856703887590653409218974871687234942350215936871374265782174012360582549759635891009261305443677350659234691411334888094583016691447506478413851786692210332884103069291530840376504431016357464401672842279159473862600445695092589720790836314505433051945268839223026728538635526261735680020640125514694922387865117641745486767737807560114356069413145843513030254057578430063498955558945235100024577603060294061771113596755818633721728098654211982059793050427304804021628754473574523763161349682175284850419236582818156064980865716476145483816198034274679778084438576624517718459301374217997767985615596748052223448537502912453071556058736828589970943263917953424626006378389407199956646994682638376389500968564930356704561568053846692273026900362154710217069324829901876963571359354949212621973636284
    e = 0x10001
    priv = RSA.construct((p*q, e, inverse(e, (p - 1) * (q - 1))))
    with open("priv.pem",'wb') as f:
        f.write(priv.exportKey('PEM'))


if __name__ == '__main__':
    main()

Además, disponemos de un archivo PCAP con datos cifrados mediante TLS 1.2:

El Reset de 1745 1

Aunque en el script aparece la instrucción print(N, q >> 450), no disponemos de esta información. El número decimal que aparece comentado parece ser el resultado de cos(q >> 450).n(4096).

RSA

La clave pública de RSA la podemos extraer del PCAP durante la negociación de TLS 1.2:

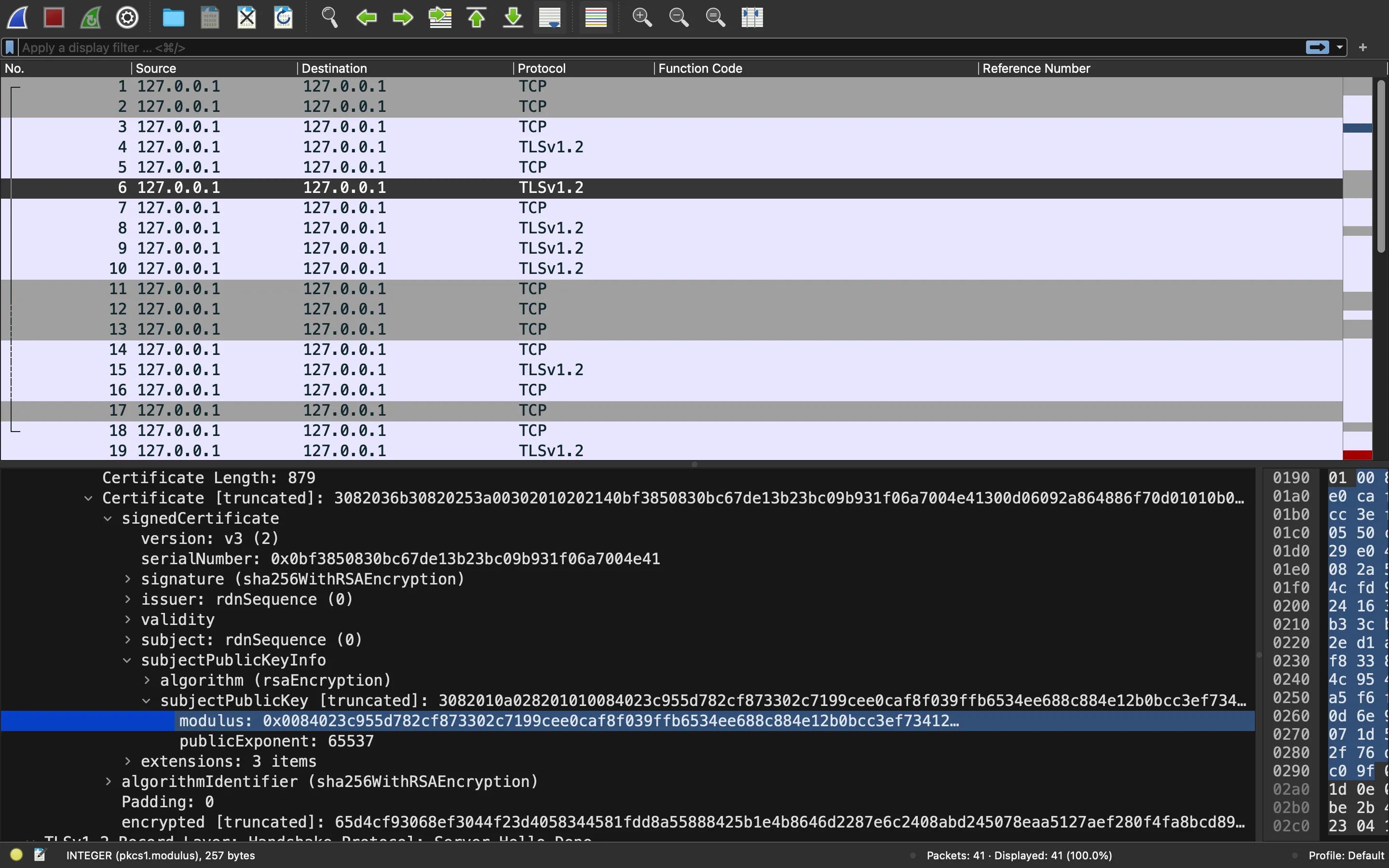
El Reset de 1745 2

Ahora, necesitamos obtener la clave privada (números primos y tales que ) para poder descifrar la comunicación. Para ello, nos vendría bien saber el valor de q >> 450, ya que con esto podríamos aplicar el método de Coppersmith para encontrar . Pero para ello, necesitamos obtener q >> 450 a partir de cos(q >> 450).n(4096).

Relaciones lineales enteras

Esta parte es muy similar al reto Tan del ImaginaryCTF 2023. Lo único que cambia es que se utiliza el coseno en lugar de la tangente. La manera de resolverlo es usando un retículo y LLL para obtener un vector corto.

Sabemos que , y queremos obtener . Por un lado, tenemos muchísimos decimales de , y por otro, sabemos que es un número entero. El coseno es una función , pero el arcocoseno está definido normalmente como . Esto es así porque la función coseno es periódica y se toma solo un periodo como imagen, por convenio:

Sabiendo esto, tenemos lo siguiente:

Esta es una relación lineal entera, que se puede resolver mediante LLL. Podemos adaptar el retículo que propone el creador del reto Tan a nuestra situación, donde :

De esta manera, estaremos buscando el siguiente vector corto del retículo:

En SageMath, esto se puede implementar de la siguiente manera:

N = 0x0084023c955d782cf873302c7199cee0caf8f039ffb6534ee688c884e12b0bcc3ef734128a1a0253f0a878dc7abf060550cb695066686bcd52abba1227bd6f29e0422076ea9aadb4093346c321b16f082a579f467098fa6cf4f199abaa9c434cfd9bae44e08a689665ae223f9d9d12241637a083cdba46033a43674bb3704ab33cb930404171416a84a1fb2a55dfa12ed1ad939c4c37906affd81ee06c5602f8338a1dc958ea4d707f82c81132d4bd4c954f612ecad6633bc3b0d93905eacca5f6feacae5bb4210eb8ff74473253220d6e97d4e2ae9711c4b2ca3d2b1bd3b2071d5066f897ef909faab1a0f94f88be2f76d8bff6fbb1344c39257dfeea663ac09f

print(f'{hex(N) = }')
print(f'{int(N).bit_length() = }')

B = 4096
c = -0.83677025469083783941541701752761854754793836436580928644247008941810266469532458996045447348443859400152817824525738732652478723578550322419681449352934903962868272432839950443728133311767399079690030001079242722034971856216464693298008475334803612328029119715730610948114017183466860376219520135065944451843458471230390067711216822465611823803314088335568327990572989813880317949003496128817743756941657517592732976171161188449564836856703887590653409218974871687234942350215936871374265782174012360582549759635891009261305443677350659234691411334888094583016691447506478413851786692210332884103069291530840376504431016357464401672842279159473862600445695092589720790836314505433051945268839223026728538635526261735680020640125514694922387865117641745486767737807560114356069413145843513030254057578430063498955558945235100024577603060294061771113596755818633721728098654211982059793050427304804021628754473574523763161349682175284850419236582818156064980865716476145483816198034274679778084438576624517718459301374217997767985615596748052223448537502912453071556058736828589970943263917953424626006378389407199956646994682638376389500968564930356704561568053846692273026900362154710217069324829901876963571359354949212621973636284

ac = arccos(c)
pi_n = (2 * pi).n(B)

L = matrix(QQ, [[1, 0, 0], [ac, 1, ac], [pi_n, 0, pi_n]])
L[:, 0] *= 2 ** B
L = L.LLL()
L[:, 0] /= 2 ** B

qH = abs(round(L[0][-1])) << 450
assert c == cos(qH >> 450).n(B)
print(f'{hex(qH) = }')
print(f'{int(qH).bit_length() = }')

Y con esto conseguimos el valor de (q >> 450):

$ sage solve.sage
hex(N) = '0x84023c955d782cf873302c7199cee0caf8f039ffb6534ee688c884e12b0bcc3ef734128a1a0253f0a878dc7abf060550cb695066686bcd52abba1227bd6f29e0422076ea9aadb4093346c321b16f082a579f467098fa6cf4f199abaa9c434cfd9bae44e08a689665ae223f9d9d12241637a083cdba46033a43674bb3704ab33cb930404171416a84a1fb2a55dfa12ed1ad939c4c37906affd81ee06c5602f8338a1dc958ea4d707f82c81132d4bd4c954f612ecad6633bc3b0d93905eacca5f6feacae5bb4210eb8ff74473253220d6e97d4e2ae9711c4b2ca3d2b1bd3b2071d5066f897ef909faab1a0f94f88be2f76d8bff6fbb1344c39257dfeea663ac09f'
int(N).bit_length() = 2048
hex(qH) = '0xb1eb9278a603d830a202f0c2a46b9c97e0563d8e710948527e185e2f2b4fbba2564309f004bb2ca615b378f494c769890afc6c1f4e7c17c9aa88a8fe99214e3bc88b8d47d335d2700000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000'
int(qH).bit_length() = 1024

Método de Coppersmith

Ahora podemos usar el método de Coppersmith para hallar el valor completo de , ya que sabemos algunos de sus bits más significativos. Un reto similar es Bank-er-smith.

Aún así, no es tan sencillo de implementar puesto que necesitamos hallar 450 bits de un número de 1024 bits. Se trata de una proporción bastante pequeña como para que el método de Coppersmith funcione bien. Por este motivo, podemos ayudar al algoritmo con una pequeña fuerza bruta (hasta 16 bits es asequible) y sabiendo que el bit menos significativo será siempre (ya que el número es primo, y por tanto, impar). También podemos usar distintos parámetros (normalmente, entorno a porque ). Así, el código de SageMath queda como sigue:

import itertools

P.<x> = PolynomialRing(Zmod(N))

for qq, beta in itertools.product(range(2 ** 11), [0.49, 0.499, 0.5, 0.501, 0.51]):
    qqH = qH + (qq << (450 - 11))
    roots = (1 + 2 * x + qqH).monic().small_roots(X=2 ** (450 - 11 - 1), beta=beta)

    if roots:
        q = int(1 + 2 * roots[0] + qqH)

        if N % q == 0 and 1 < q < N:
            print(f'{beta = }')
            print(f'{hex(q) = }')
            break

Y al ejecutarlo, obtenemos el valor de :

$ sage solve.sage
hex(N) = '0x84023c955d782cf873302c7199cee0caf8f039ffb6534ee688c884e12b0bcc3ef734128a1a0253f0a878dc7abf060550cb695066686bcd52abba1227bd6f29e0422076ea9aadb4093346c321b16f082a579f467098fa6cf4f199abaa9c434cfd9bae44e08a689665ae223f9d9d12241637a083cdba46033a43674bb3704ab33cb930404171416a84a1fb2a55dfa12ed1ad939c4c37906affd81ee06c5602f8338a1dc958ea4d707f82c81132d4bd4c954f612ecad6633bc3b0d93905eacca5f6feacae5bb4210eb8ff74473253220d6e97d4e2ae9711c4b2ca3d2b1bd3b2071d5066f897ef909faab1a0f94f88be2f76d8bff6fbb1344c39257dfeea663ac09f'
int(N).bit_length() = 2048
hex(qH) = '0xb1eb9278a603d830a202f0c2a46b9c97e0563d8e710948527e185e2f2b4fbba2564309f004bb2ca615b378f494c769890afc6c1f4e7c17c9aa88a8fe99214e3bc88b8d47d335d2700000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000'
int(qH).bit_length() = 1024
beta = 0.490000000000000
hex(q) = '0xb1eb9278a603d830a202f0c2a46b9c97e0563d8e710948527e185e2f2b4fbba2564309f004bb2ca615b378f494c769890afc6c1f4e7c17c9aa88a8fe99214e3bc88b8d47d335d273853ffec0cf7b36bc4d3095ccec142bd53ef2e79ecb1ac926646beede6b327383ccd62af2908299c4ab193808281b330249f0fd4e7d92f4ff'

Genial, ahora con este valor de podemos hallar la clave privada de RSA y descifrar todo el tráfico del PCAP de Wireshark:

#!/usr/bin/env python3

from Crypto.PublicKey import RSA
from Crypto.Util.number import inverse, isPrime

n = 0x84023c955d782cf873302c7199cee0caf8f039ffb6534ee688c884e12b0bcc3ef734128a1a0253f0a878dc7abf060550cb695066686bcd52abba1227bd6f29e0422076ea9aadb4093346c321b16f082a579f467098fa6cf4f199abaa9c434cfd9bae44e08a689665ae223f9d9d12241637a083cdba46033a43674bb3704ab33cb930404171416a84a1fb2a55dfa12ed1ad939c4c37906affd81ee06c5602f8338a1dc958ea4d707f82c81132d4bd4c954f612ecad6633bc3b0d93905eacca5f6feacae5bb4210eb8ff74473253220d6e97d4e2ae9711c4b2ca3d2b1bd3b2071d5066f897ef909faab1a0f94f88be2f76d8bff6fbb1344c39257dfeea663ac09f
q = 0xb1eb9278a603d830a202f0c2a46b9c97e0563d8e710948527e185e2f2b4fbba2564309f004bb2ca615b378f494c769890afc6c1f4e7c17c9aa88a8fe99214e3bc88b8d47d335d273853ffec0cf7b36bc4d3095ccec142bd53ef2e79ecb1ac926646beede6b327383ccd62af2908299c4ab193808281b330249f0fd4e7d92f4ff

assert n % q == 0 and isPrime(q)

p = n // q
e = 0x10001
priv = RSA.construct((p * q, e, inverse(e, (p - 1) * (q - 1))))

with open('priv.pem','wb') as f:
    f.write(priv.exportKey('PEM'))

Y con este archivo priv.pem ya podemos ver el tráfico del PCAP al importar la clave en Wireshark: (Preferences… -> RSA keys). Lo que vemos es una petición HTTP a /secrets.zip y su respuesta:

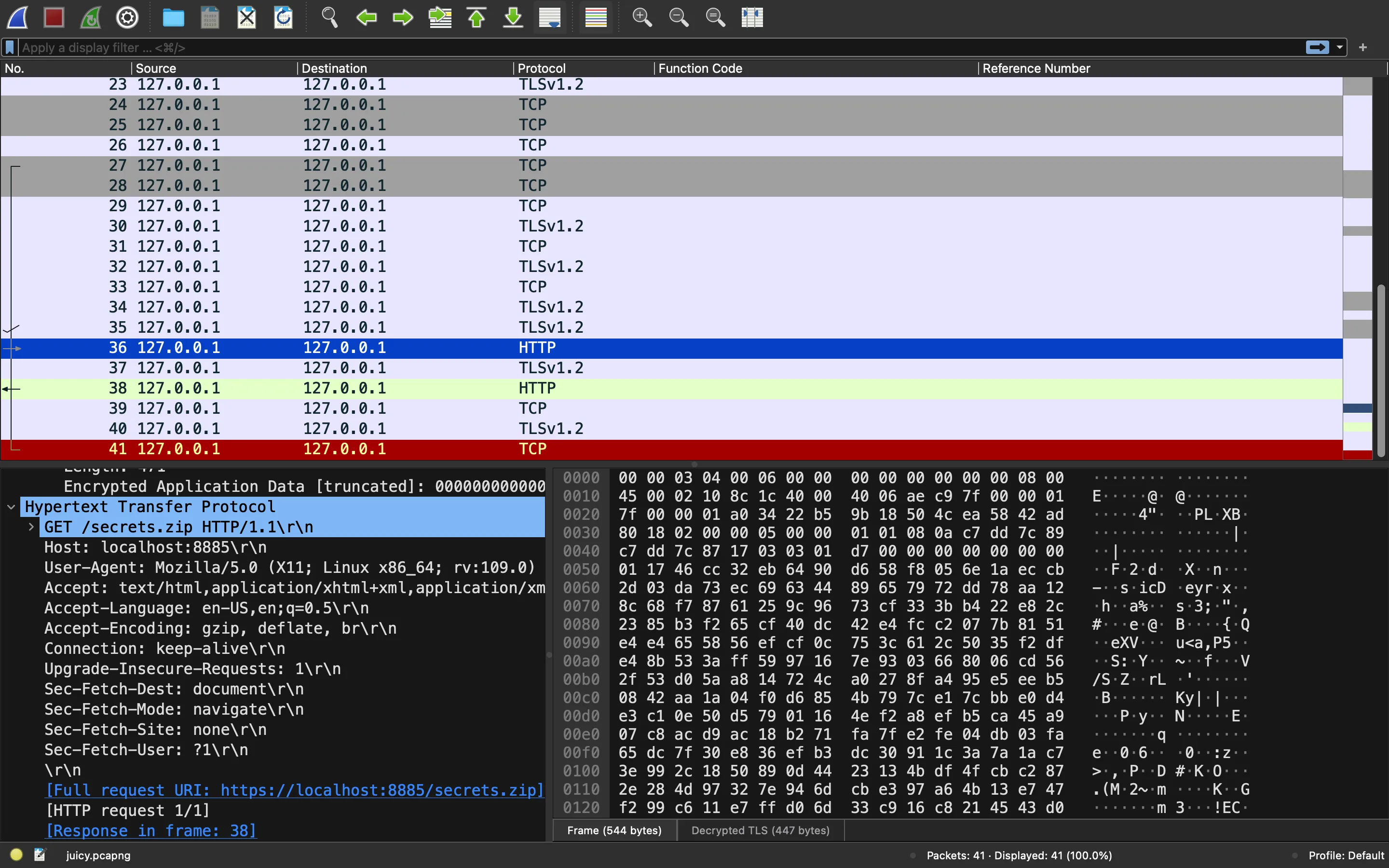
El Reset de 1745 3

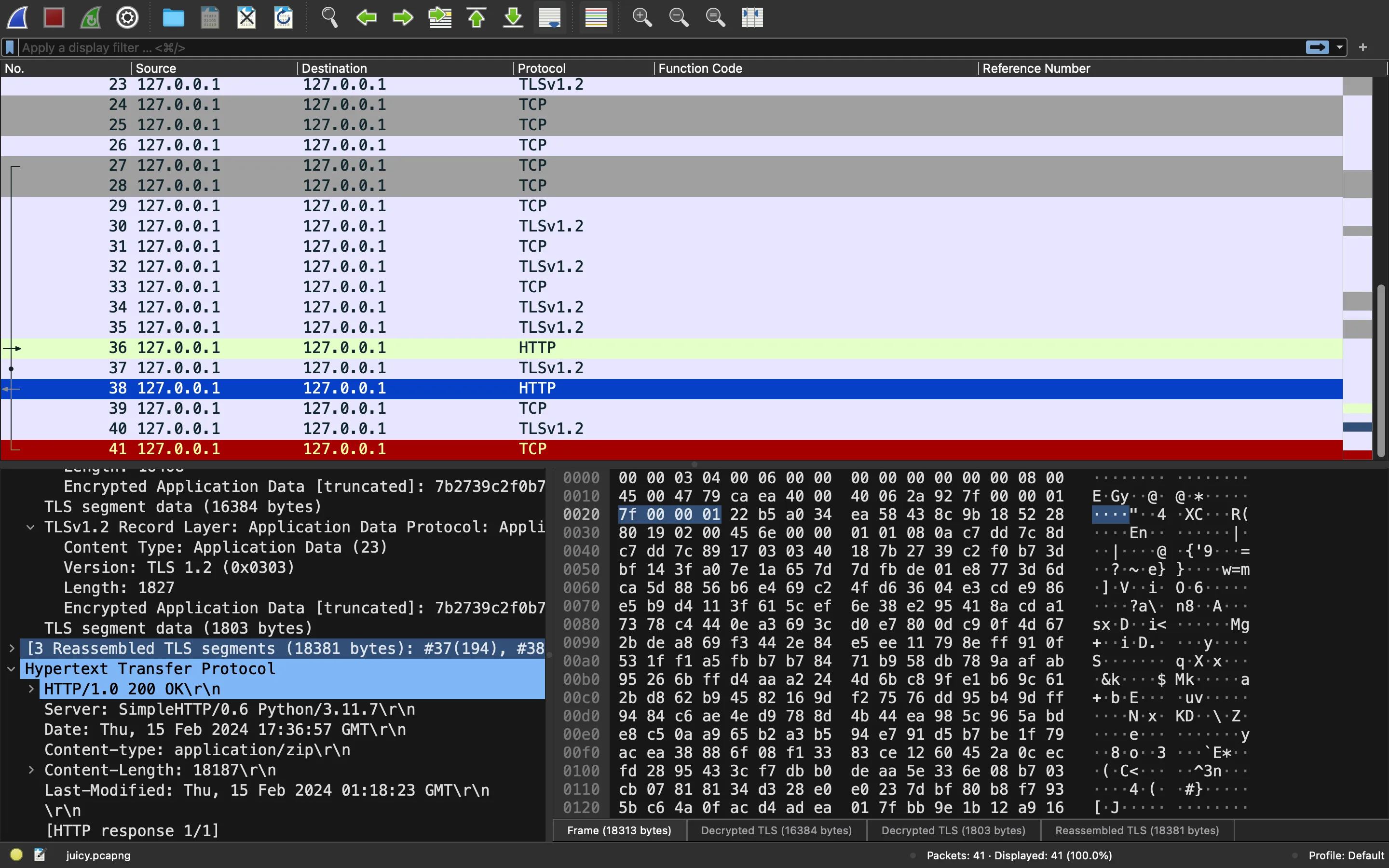
El Reset de 1745 4

ECC

Al extraer el archivo ZIP y descomprimirlo, descubrimos dos archivos:

  • chad_encryption.sage
from Crypto.Util.number import  getPrime
from Crypto.Util.Padding import pad
from Crypto.Cipher import AES
from hashlib import sha256

def hide_flag_between_reptilians(key,plaintext):
    iv = b"iseeyou!"*2
    cipher = AES.new(key, AES.MODE_CBC, iv)
    ciphertext = cipher.encrypt(pad(plaintext, 32))
    return ciphertext.hex()


def get_master_parameters():
    p = getPrime(431)
    q = getPrime(431)
    Gx, Gy = randrange(2**256,2**257), randrange(2**256,2**257)
    a = randint(2, (p*q)**2)
    b = (Gy**2 - Gx**3 - a*Gx) % (p*q)**2
    return (a,b,p,q,(Gx,Gy))


def third_dimension_ecc(G,N):
    garbage = [randint(1,N) for _ in range(32)]
    secret_array = [garbage[i] * G for i in range(32)]
    print(f"In your dimension you are able to see this: {[x.xy() for x in secret_array]}")
    return sha256(str(sum(garbage)).encode()).digest()


def main():
    a,b,p,q, G = get_master_parameters()
    N = p*q
    E = EllipticCurve(Zmod(N) , [a,b])
    B = E(G)
    master_eye = int(E.change_ring(GF(q)).order()*E.change_ring(GF(p)).order())
    point2inf = E(0,1,0)
    assert master_eye*B == point2inf
    print(f"The Master Eye is granted to you: {master_eye}")

    EM = EllipticCurve(Zmod(N**2) , [a,b])
    with open("flag.txt","rb") as f:
        FLAG = f.read()
    KEY = third_dimension_ecc(EM(G),N)
    print("enc_flag = ",hide_flag_between_reptilians(KEY, FLAG))
    

if __name__ == "__main__":
    main()
  • output.txt:
The Master Eye is granted to you: 16265471931640785828934127858946752538285468297743536678369884769655894080669562147795213991083005768993394358509783223221158858616114956533429224780974963093860223870869151381622793452378040102391285088110131930993214655276327069828109098832154854719776594644
In your dimension your are able to see this: [(79364468785236952279306319947486981248865881109689880151701940694064893979908366213038221679380344986127502056375006658490264731158574287241753313341555481402017633356285197771242603178001464846171145411665369899716221278004315749554836475575261046450436145959429152755593843874272934087644242937261243790850746058845526628319552492967085187705098606977143896792510184949161152227872504750529657542182084860998608178545130782929487362604009699589317802551001766633251821245604199207911871496973183520003360060704663214, 16687868136816790667937853246796901063040944936759940662722448380093920072006750947759005398743346758508016260528885932320663505212977936388527162162700995881129762284545953159504084714702981447856577155545734415853887630161403524590482445165827667785041932424914364528689537173920286382744504598070079197190571583803626137199250536574114579102857674775519365478519464262272039879237629974345129100337321029345797122618346654708409642719988452075056672175360303595214679844777756177806896404220841682828148652726672638), (18899724296709356965234494619104772779470606388931481117456688008818773207217366971633275128353972861633690819420635187472982517415400458909499316310931735946901572543121761179549512998697352800479852589929855627415400504246815106263800422957389670026191418168234235240406098997159721205877122915135525815565333680276051547563185321448352067894786538244048272702500927838999047658003300634824432270546232541050231457086443144424139179909585041352826454599094625605744436472796192783054911539407677446501812033471321524, 181969980377542764707955040897437722784709145520407120692028567222043813796008600849964806554297247610034947681294613264869782056823632123233711963621923181395296514822877676280308872426739819929410735010216364608798913264921312771916561066019134544296445889808932682039938044349353633612260789631107610936747968998606077205378127104320871869801486116872451256587440551053631039031230396157049192240149053601614033999746393390194723403360681914729802280523975083933174774134319246514382925460749896675407154805485284511), (68471692495575172133443182331265395323780023618521247524518268730711946951940988673749804251758452778660185511305483225416051708878357189530595965992350055334820378387109046064384283138464825854455750319884417034907809207922174034293151428401066968153603720309881678240489554389902246968911783683529409598893006732050710469464502354213081471824890463157409366264164051370265213326073053285020204917375631748764264712643374983681057721917952358757015432749432908948261428353275093151790075022197714189206163134215315103, 21086153520048598786169857750936805604277664567817774664460508684003670502302309090451996890460669084397056007859256108355293069289180286744069869788034455379356774892426063355812211938369687363613649187261276214647682224924760631173273646480179734923052819579729206566136998202738004693357079772445998313417118811575716713719713425456903643208635220241330814329516583323942979855886550421694669869092246154864251064889038193612822797937736925854371199646805580554872113726878535438082715356751200540213482107525098188), (116969053282694964799384771184091326303783633954428385196195106448482795095537983186445774516345149664381173834220871423555644858263622043970631708050194494865598220654365692163194726440427226462426292354441330021886333830775935143649055408074223466986424355324037704727682925776252702628182654864848940761049870226530117740598115594078111417658004448199672691637414626676511064717083418122102790469776547004932065495742273400807655050349768888802235266816179305399411904017010194674411837318963119660814179508659522079, 50084014889793959696599960870266488490551570031242416218275044365044406279560773812159187876069277424936558566002408934269450009685126762919422186537900216338665358746852202216630815904714706257229182538937888481607640416939802948615453184222442533517179199989078012953988190237579277262608278898391324918782630916840313135675473154777780855027523835253960743640206425166079504138147039127770593334045531030931479175201464964155413852798543401227075673058536367848947304461742267492110565792799164008125042863814750484), (75495634491380681480755034982641869190790206884849110723256175106318578661884367627647143036688535570791725909016139335131090112769001955747766299722705758599159778181042043453667346349033547319312262250475534057045860453347457133690528259902127083849168115417362595686165076571790325723969187880950829034560735006803713082244776521462470725461944018138446316622326672180314948459934243221388622927753353641287295474464745004329035876313365899195265984567422425276920658644349603345662940685219340306202950650607462424, 36253213840544424135747639984625468377126489352389007053380932532914480713717870396970116475077843047531097911732210943486983201258877192757861153015876591828621816348899115209925885000722027312971132000986223661591438360763777219039380763132328418089417368883034318747845529041436281909436209997433288486880452129344883136566180200589020934893263313246425182857484118510922258585583154053518563004163870433471783169696048347094801055344875002707558347225173012259302506287684325108055470698444963530011674895234940861), (192481455040907281329193584721852105461149835280168733847414582510382943795683937046047272270386155455427903029708072280124641608091666028101203441908633497627017890386867343567857125870268607159026410298301416630232047646360786504167687619545786494459446199856135388394976238012143847784593439590750118221999002429721920816932370398509030842536157171976181011006850034186822030054621552078384154095398615589672184024311433279726791936051360592141198012580769956217276136748224000824970866935881059774801322488495734737, 263750748030593406555372960075339347959501012664293859999528761406646617202885255209546013672103696519460696026989591318113562143370752757504971207850886357088200588529406714681418094672394611241767914354242709867737587173914012871284335033363056451884058022592279355794323391316627257591556094592398182461024352393825325635906355111844626491458756610991526543618068466546705753811183653095707925663763039824680079042497299645105323384745735490293862452599416389420082263130648481405274914126094178915535243279138216891), (255417412247910237204056992220045681879601415453288901101493272549214517912477637905405057604185717193019107588463580766046854561097661737623152334645649813648085887341524457445897093708191115078479102309838323390531754049310253939778322042103086681614882877414565503266734052030713798844268300288931266616639070681932489338231071158921404363210396384266907626544529764539182475404302001747080341642167481344327297753736338699702763493207235894318368979448459989566928583831763472499113910984819179772191593553652132474, 216838227007896475467505545385808596622593627839947735482086337073695133835970632571085739743178459369081219447146261545489025016023191480118835913846110397255114648919854819641700710717424878468620182038420695530305995881014362474635138548754798584240818513132332952780471786911557099270185846735324286244202698215309265097328428369735979500503151382847521451988517209863599729938833413473246217315543633075429285724935075345739203874313074322507039546739903067587047347937253792823522407423759267865629674811587336735), (124096126188514803544503955059315279141132559829237017973895020854171803237264834921222239856902238141179876125883968947274872965203378100360103207367714763024384163506879494701103972703086350129968586526203471429720871699511033522121952069111450022016969221035561423806264769591980121521115751553028030488337106779564554084983419507958422995036643408111208147569385927747112032878129152578402922719412406569384357851502035073976747328543651617464058989532223729123880689755690748865232003435467745311460600569632062195, 79795929489497405541344074279045484311257046279349845074266797064963552718105676350112801481079796697379543842277745402508713939382393071567528053085584437224203083580852710549037874369323959513137365714211165782436080036247333330794646390255560519641038629449067754438673314304868898813042624277285756041579001910407073190691633730020025977695329396764438605452385145610146775049817517456197497958984225616236669698260373850993781035376644766912592244717606326819474841714478055835222357317541164073792768197449976805), (190703286030345244045469778665561974216325069308265949202325894850227791765904139485525133899256922401602997366124011248349376295580261874319338852553684877393759367840644756984940510336404382711261363588684354508782828978401315935725937405785634244395621036683704621600788947421051146412108450650360926888325295167558040472336174751620673578392573280408257149796768348815768625550159870118878124609165630736159309639790673200547390682579251405402083531773765502679177847618650304506944498168089416322240738303940653213, 24736645903036881803140323581228716611113404998832076832196705758532168994501238783666375149022287321792427144500995307601858381136965807435697339506741211246927952932690067441621139167964194664193434621736623395830739730041951079386866340029257422408469503684333096054282304496745395068380277705022308880154716936569675145590997527120346373478094696152761116815474531993309298675688562696276172987521492269383043279810681588686656859154216730700730536263035848904078841458919347823245082214554180323650026964599193449), (258703341869999263552696566941924062917262532623427112981841289107534325684990395930426708646820618617158698098807584327410715882613007054798579382797202218924771823397597250874444158233109489433439437861168171982652882535734326225316450293623741694672869263741406310745286481287471748736505002599328297372513945104194558584930703398823479254727890496522036645921691948539312161687230707649623943993196786543478056821803577376429265789558098025007309268634834269286613805213473295723199595802084698720821452641690348762, 157597653185058333749305618814281541720926026316916248894515953007654834382945318302782897071081232168734135231503541126542944853455636669320882162239580132818141369909385380309951303769335111171767021649073648211864119796372073673232431330520655857858471659683744957380388861533423069333178715676730080139275594800569694523547635241524786097810950368839577943317787129038527925602633331544524871784599829599691035333266868107278941473293754170485781398238637499037126629714954539370303741202156428560403509971269120259), (144029484484143740842105007898750587818400259866067203106619661765763196612852225351180802281798132738759712673153837981988639932431947090809824592374750203985082077932231250238993558934126045641958929154545019638665302385408753639772238214965583998593458523982768916457289049350438036003586345084629417537221581589792274874386127526724174033010886505160380617273573415323932040916826340570542462697219927548091751481509377962625757071590735901774613456978510749747386546939521455040718702532592290387855298509964335504, 81136403803938509674953360140216723808828994157366853530661289992039975024693660530412770844694016294799917019166287093752795881772713038987632126846487124365054635128318325215698759027661009762825117366778570281270937841455064304807681267714958371425526732088357275832549199054044120705515004113312778633030563138690914909627177849996617456660673293755637236050697184282677574577668950305536160357560245868725179346462569085515282246946818804551864995963132631326540113293786152201453968620257820912842230789280672879), (167933423643310489968736909399339291074532111423728809018251315108934196550988975700904712999504968918797886060359964419385418362138089494181042173732835977776288115501526781854180140081384888294467362388183968192889440693933788263691009913440459578937986555297497010971816134549682779591167883513859028748417671900766328167176421597712058150529821656694452760283330487597721120507927015978002030880379686393503772683299429146980224934216236258524809257894318690697716404775604790364766740110823609354214543678454335207, 249060203030314638656800525340380123405021821952904721849953191711065909060250501335838898260047436743185888780451959829884660980671620355155805987888739105567254190879933334691411436378354628161756038668310804522041631705561214001778546633300265947270561795770260431256098931841216149131420253712922540548278872260455771972510899952597837538488876155123609496441312030794339392252544212884101476954780198469300130297678877552887865118112329028954549930740352455919380615142366214732987382847820614960930054016512403685), (81531132387261687911917499446685797723971871365375671509000262296850261719634523323876587160746818150479196876938791972820817931157649714415936984850766979784687364441837634119019081500667512591299111427780436432976950026422776044193795432616317613520986261395626116948865296824517463828639995464038528157308915881004595745408077589331144910923977821241124679034305505478460626044978730506369719002450030831539905895506531403799691784318024460051225878101146939170314725597099259252484920566074712476020128146708728763, 2937120054477468141509617584718072841466725665936920849977929083765990055665939440305887249811696047078394520908428092839293350858414170848178164083344045344698200810920746906003705786425990783693973403162815180341354385994880845699003303202234732248708097094724976024552659615350213712717065586514234121293071473763401980455740807740160917980173788010327993607060642470248510559196661609000914685808353954049312164318177565333183579224288193591968204930301057232213051631057654211493148123839424779942852687340685859), (103644260861603589957248808023254195447470005051473901151854421472615182158114771695576397034699248112789770191530282302797868406969984836822917079823398511974177377027477715431406825405053605595879747122357745078872754130028142971701445852516659874028185272404314555307882576155287855648800598012051775334174420913382203557539801927105317596120387809472648928484865311968302940472396169283793012693982543833931245644607885977240792560196956780193270009230312161519165925549238619384488289402663988278459288965755045202, 13386131823381627746769871412188175354099500837026101545007050182395652213622116827516458708885503040423176624137354534217799527216400345533053176835186505390864762712683850484524757574534628840609687178597044082451530395700669918033403997664280245962765624164711393899615828305969266729155003151307376498365166318455594869316786666702572444740194586528840860391405316667797716685898051306351300068423693781875048265594832229743511143553177543907602987672492835074752327279125873635511855999185175110114329459883377537), (49806447733446335028783340650616199033338438619086297731292629401023714767537877728133378993911023452403002227083159364255769432882774341778909294590221930944811276789872595855728949386605648638168750044129790208111103100331015942951240705120476205432357062176913813923085615505235799335479085172612638542586397849084541871749283790134400068035128471694535143019228346147248907280201471476695674163387417128954358898944253662151554055947196719426143186764729676220385474455614516558327773933799259609604596713816808540, 67153879925391225704783520063321728291841246303771866370802949117008384122412140630611604172020608684305418836497124227910945398307322662493354546743254952303151830473091638175848920166466803499511290396766988373587222642302671831397081157040791215851705427492378162911106643097070740607333182057088894418177665114567377267999038233912213229123903048082371574624240893841173078444693780515417133220692841998171028137554861232812549476624566311728736485760045414080572245456064999665273894920043788708634808692721225111), (121259199659160450418948388268391671626763025328320946113219792501668203928186402325839464256295141580273373580230405155605770463172239061805223622554363862547879300443826551552724595822125684018396490933825583005990724827277076614006784797779689099622702460506413009438350060304272340392268432807413132707604981714652259643802514139444520463112200299452118287602493071775805573055176357194744688372487796393645874066138755543916937978565303290845579555253269930091309454226581952736942651259771285494328313841696719176, 54423785383353167245475846055742639414462824811528992154255919783122213594530026632096607760980193960486608312853375968958284421107224238091920595029896291015596986820214401232689927476113723708035744569656886855911932772506245596347237606736702765609624147987779604630980992572618251242821548630723856294062865887942586987410202233110518443350460787360988488460220225272399530872204640419820350367837356650390876309151879191299124610782813723570535829463907264642390350356162471637889917462673983296700274587307954465), (92977303619726373774401333534444147442488907995426361498879182990025454415553018333510508171552601209120558825262326946206424684031961499092804928326240295304486879568678879403499951176191105736205078630584013388298255658637491139786884227468870908840259825869871138175305278010052511608139487753205231824362171703992332827590103700189042458984190221436070514094303300081382771155591123233515363366709552805738441658312586231620217316133963684195358526529253054377690560419819547756625965095265987708024421058924420032, 17534083239981379559980686853294607180922082121446077383464277173041051133747075976359326283052436801964963297772275562097872932301281868876431190065920949359745987270625836847527970947817991199732508451593735881928613879776080915431405451290973033569319514193671669728141214871416017947828875927229222881168169257475334995978506638522562727082841621103377534674314230094515648566698775749021699250522226914566251601033319352322004841943102716282077117990514212749731767331369952932713217468397590156019717599467826551), (151714288904469334580506311699687786932470047567590570627562909313285345196856604545832204480874695065076751985948503804773320989285516729101449384425625868713665574733542588482486855117947345613674296154473648201573294656067965326647224949611860214628357359309132040214209027790777151678914123082601456378886356732067541268132080748126762522835420758316631537412494961049197204205425016010352396151454741704273031546867105807470915616417638914866181520925045778461950631479727411682307627799765986827626393424093734894, 113195138575713276051356285353595608257964537355789624720904791904726154999652921625323202826448756838634725794845270773644628040704179463307506514170317679747518970223913451987204840944885539492431928207306649322098820553336366010453320453438302826748962194453073126072743462627626115533593121954332373216153303456196916042716877032156444624816270538578390571230115119658190341882710839242167009432905590403357945527537819618201757354986156989592243059863622832218854572529390202728216950457641950272095047333787845133), (143273408433100301029438629162157732007505901763968878422325872934638796541841921963880559171658699771599739944152860051396803691318827873678982069208535949317553094600976400547016789455183839578913564138947854902083200750061811236297222300037227275227735722169533644406492707041807445447669789156423983937337719273019297023253445936781670574157403858317609232724531493177053685096399564928522819896437359216101466084634086335795457115176098126076627222756666882660350843183492723945161110628940344165059531642659523383, 146674949633658124025273827347861739617972591213255422589451591241575751755759465692501605421798064451279436966144748850444994638018170033409916882690257065465451494369820928610739864416954101393861243749516295000434508472045269683452155382300622934680549683807475343006424675084022636524729510032850421728560842788745437895154746501644714259838329525121421521371090662294754870193345645037618193357860641995113251403596073075572702204621066922420230140482691977493775315013737307525071003333168203735454796604053833545), (249403491506281311380969267380571404400571727185603034767598580858666786446738167171913111309031464069379363518911333160553855193326393702713315185030611815951152637452746142527720323983558876002146517342279115230804997355865418057903304497673749142638365374144470739441077179470538767458050046177835858994825609702629664894934918018990719979984975720592480571603874761730644357479552994821055677150758155915862526298576933222903943787581240032930566464815465204077024966262935795336546362399011433775662246247111398239, 220026583481159087233455062019670620573362768860109890275771463721572578698600501321802550891913369288645565111669790293890107298985819301987334470845204887838326523986148919044265423495050278621214141338819744106934635120845496939830822733488219002062348108603935860045393020164701405072467539274006065291082813376084700667518290775010951235883727637485506655896607963039368820379051422268084714127890377382608847667294781936288634493994597515091795456078934847649806729629586190284753683050015906539243957697001022023), (215079273711572876410986208369683751294908183118379806386470679715006826521170132721726567905439942811382303605708056664603360017394551900388730088190217419850878783175574888901650563370610979038087942241376746471780988908912202971215079064900140401113825730922891606699754858802818433393292483508699051884185015859425552120339604916848864621271989828730706632512180758062407093767038158443746033606152375556179657992769575646334869657982412168590556206097067487695947784501185834313278349861463587166621658897486961285, 165567166071807415210098884820764709496153202096646908950619075676969166055854408565385662974546628510018441833788996418834797201726509458995351065808801225062402256327061845600825747669765288510624735507443675920510399006294180586052938942717561974376882538088092265694134635957495100715662266267357612266079433484517807375368429704206604635121324513004453596132019914682211594230617872219093487683074011218155282605906006194375075803005611967842695926548707579195433499994415413239784543530160970447676692869869775676), (228640244303908717297167044778358038077902415175263705677701277564554270721639076536848778203545648125859327404830206543807475124805809333701155019527553638924049712539331364884394462007690016542789938920025584886621196279327226524440087499458342989252357755491410890483133060523953494059732343775334979996866384865935940617099927020557347955903470709779090391882774438879675954149657556507819136838955515558446346085651316020265457443778053298058612260871138738040683307567599833900424381965386410969307647307369384337, 50165978141277819866049506699428057948802298519848104269621195645506935211584635274953826734316042747547515285609143893926944616496665386006349117172998096582280910144517457297702276740861716885437586834114054074206762165813673080314532603338459131607867567911958178781739505569816626312228165860061197202805933649452157563939564094961259760708185312146707171518968545037144370645198264879962319609864920134620742014988290980148541839415818403783076111150948944201550612135282717822173823751686257249500946118268104684), (260772944033526649752040603039686583353866815340829345188533891968004157467437167053710372219786485894088629376882326037936018907830890211870975702462740982328255444349717705245571849629146899762401559087996404759952457290427825581600106649293512652464779359266335650503918992764721684994867827583945612335934204038413816090349940775896656941750661067477541878792538967929065878101983413114812547001636708105307101185316535811926701056506444389655899925460725232919103379480543873872663434597493298813809089638160216500, 178822297670557205167893884671789644494733002710980842013844409963257117977727466427973839291798664502187859871290871392663447194614632215617775851356048586688401675157884835686198745209102861687009247775089840237122905831291304107610469327023876013149997285955560827672550035934501475882105008318345702835710511139568555607450691543879827538078967647488713788236537917448993732693958930584796688889209027167790147994500386404418863068804471331354407391195350272032834736051454815212017456171393538604058440084178785138), (153951520673385600585961203675637598772601638997436454635342055186847630642649668335965719208548586394720698759337915374432017680802144574982195131450687416186157048436598230083986127273557613203138054681250267787104668155803300164220352768363677389975389879906251331431662461990044058915429571767891876553813802059111070091377174616114219840922496478719633748862558761260936593076772050749815146554186743403077990697502097617642694431073886078861243520255713835477305063044518118066338897871379418786916048308001969642, 156677641648933384765684691841278862645672754960550364491841534426373366855026169555313043450342179770319758154010346709165462884527668929783331518815234286818109634304084831326103818198387741069702702752332554903172870825713486344211463198732464292089738363752466400950781915098607771340376959222392923586445885108829631888240542595711945606244159113099631894036295416012830825883435869636226984125330515770450372976608451137637329197460905623926500239295398492662897852793832046161329679123965719170637821852017541626), (182121275786448274703764860722207288688504251090526347386757201912164299971660589134892392593241000207363015377123532378065868724162125833912530972394915958665480631907067587572014039907112757035041814867937944633329495525743116952775108181544154895419181248880103117645953572669852637658173135330666489107513016628573955811775466684165143992392582744844394450653190459150090420140982302633882320923586679381748714431459394022990660732442705410510333910511438790458145935472292717646314404943912425265028499888510174598, 203440028868962984833821327933789556292629799184980205949050297313869882325162938301832971394230086020203937893809586214315999984427107160219912194805861777145741298008459998847103235243151628211509976280466653813611751247864428514134005135222162797493409369979305348203986570673847042670733283319660635425580706085693423174093318482780132615052711623695122664139057281605247745929023719568948004049990752313628422178360038895083650988297135247676372740583180753811984847210662578351383128821641159416840888477928682078), (218823575478368993955048790301926838437881143334348547262286809656812028268317304117409196876147138768171269470142474896692100140880755219823221990741488174315700621873115881799875553774369475082536987154562339321080637214185501516400621440388225723796980982899499623333730581949456459563202708568004908699142703905181478123703124547955265445070084332319889770567425486299504192535917180867591651719599910708571157067795615339103935726452179859088482325394789423729638822803813023195364259090039516707595275620606223098, 238360831921645517033282852001853402704192593646552818549162257086131847495832206207536403824297663424275603654870000653597808272307859106152007825595353459253005711098749795572570443393454435526757269349583998699531628152424144085951574812986232887851420719883402359586733609130991895552759814577684367961852962954957142339493218345367856462618197020620224169353973697144908034084747802499066704624535556265014878529090655506836355781206186508004035222663675445692924362410085183466479682020421951634577195038189582468), (7605308948924713893554832066864121414252483808305011091620612954856641658669367332357087398584404497275705301412227300132578417133173046053080772734818034453592192660914525809258158102936364260896213514380057335541283089086072298851758871406982865424218623716834685065557610594958011992745774101791101476219252968301741083316175066203079039213553580734030289747773949653701560564634653634860835561109658488968900667869196390219359276163732091789449610499277368225539853863255513232114666428859799256253673733736659934, 84338265593158215073600285774268951532171030715482815121324903198740799001477695481022777242719096465783467452535757377773297443527190828821051666329343779990168147101359925275718790254346877292701611345915823716088047741419538003476861653674067582773629818569266305858464954225803492630796727802186048224313050739888896540519497030255394106498300870595202213057412239405023629489623432730026664229571431460166590904128615265134596663917268529201962732873572258496676098364394367451264108741454944171782819942195095341), (260574236488407935488628660869550896326797079442686943514628661629687399953873851351524123117678854245330138146883940465164632401241414354283763993006051409910547635993821167683763784377300171479035704071118316710560399835534541136502396716751872135374863702011670440373059039486855344367530019761146394096881285791796980662052288525887698305777038723190087660859458441551938560031917347933816170298126009833562473518886720754679296740435464958844554206717306339055626973734868160598112213246395854439553619910006602141, 215031607965289395841597958782668037673484825089737077680116503967686961841667136969161392233440749102334833530419916926904430230760368898665628347399517114710948182534421920881834061302840221573802306449366480749919988514946580495147534756949978412713550979077019198599738941387116501782579306035864628214179812916834096486956736908275485194857938819787685023366084861770486853029181761022412161076373564613780204140998658159981842030287716923797731294561007312770312377377200056945449000311171752181205441965528935874), (198650576114165882449288026892214156276310958538011770523786728908105721360166101586279901877256531212257550264666494397314854415530372455940040150000010464517188336179827548221813135688964063397759290819652552869032850475218576198380858804434982221752101529325232884185525464193387767853411736259300751746214902051788858890055001236520152969180010172699764643110516920458462497046758742780733065725918173268086172671600452269919046762751217264939972190320714063861500100730343214043940778545664923273954431822712458287, 98575677753024287556019342929363679053982268955883779060795868148514132469159057938577626286714738458880375542997435176228749972239849021765147899018326553134629305587630983987645333121909724303395753140044547644366980019247720029923521164816180269979075442608444144431202613744990379185147853120702658487250116464883053687214761782785364318531008585387852132690487409708623886477690527271931747982661236178782523900957816260304362680211164984895592121752024391716149630257731393458732924761811426589241282290399095942), (133239237361361811696048540847458002212650695618301830827793891053639158166896674746134234523487135397403954524183567898886271486999571641531735158385404357658102658615539986689461289623145800299293935203492505727751870154133777899999222627625429326191129944696381042246624406490311860471634501715534659706946193422960549385790867868364451316422996956308516881589568763130787648575177095185336254852857468636860618577916534359157560688439784211466848879111128248465929528606516810076772919357973993801977193176114082633, 91993476954022760012798281670772708974247590300533609094245183822546756179517685689556735104286180548746323121584555720933324078992320978166897622353779701361126291322413292697697396543199293764590408581810818990685090527780478292097542106699940483205806149443174482967568300230425843760446653203856070462189339134604330157898491668720364014222964691584546427448260833308773860654718614894674905336051468516174232055942686622203957221449760803027397791234923638079424420066167267329350115771383830077528497272156638506), (95582621179135234162644663973759115030280708105173042864643748820898368161340863849390296104736276377098268450466214656481306123639700508027953901051290602167543644403815267941649482259183013123386204623097548703992945451692699742180719629475227930324881627331813906906508914901060228391057700936398107111821208803611542219630887301456153687209236199542403045434348094180112509184244726118896660624616403473132543257734828812611125323216911743462747983375152094663325459065388691057143880240380997574071376853464247035, 232352441732141135103454694828789409695750521085516707673246640367598676004047358260302254213092756665608390600758286850148614086134444187559526307489875627257575726111105762131815461870322981755137649000376767125396510619885683103239625485770683659802497093679638121418808084113118832714735551581184248380109440381623813485630097624684044974323307573190413869646763288463464923237420994040221148913548050627902538591565441845343995830686332202964403908307760184053940232271993381347882801989168889743238527356213855452), (258077403654756237716504509389411450264086564167441197441992247041683977605292742137327564976821856572413513401676985367106470072675968010369293214122880029016779939107521858890678568060848094862941480840987133595171797018800289787199783252896262873627767237196210053178254269524723135216496799679281365275621756340432147482265982099094739471498473746177912190376569719635941552555622213874734197454882799555744886325184069583870028520520148657134565959771591400315189969688904284018357614841113544340835425223265680147, 132619711305230755023718414178727374860129372168380541236154544169652117680402142337603417839580343610412910242758120828063112527040245594832613214330126362748191108746206127128051213878124100598393743003465997856657505974679274302377336989381816351610608074708062960998916948448170373532794915312522943031887089971768553107015227988908849150040972068906638987306481505099609598863656873588776064450399947837586887592565715213866014274642313127496432902232963787467375168488326815943797992382485889955510144119668259991)]
enc_flag =  5d130cc326373ca55bc593d06dfe84e33f52b5ef0d1eab5154d47c77c502663bd0a05196f5ad666c69d70ac94dcbb58ada1da640c8df212fd85968ace999e7c70ab1cb8a2050bbe4f82a570936e8b2fd5bf25d376d9cdfeaae1f94b842918ea1

Esta es la segunda parte del reto, que emplea ECC para cifrar la flag.

En primer lugar, vemos que genera dos números primos y , luego unas coordenadas aleatorias para un punto generador de una curva sobre . El parámetro de la curva se genera aleatoriamente, pero el parámetro está determinado por , y (esto se suele hacer para comenzar con un punto que pertenece a la curva).

Luego, nos muestran un valor master_eye () que se corresponde con el resultado de multiplicar el orden de la curva bajo y . Y además, nos muestran que , el punto en el infinito (en la curva bajo ). En cierto modo, este valor es como el orden de , ya que al multiplicarlo por obtenemos el elemento identidad del grupo.

Después, el servidor toma en la curva bajo y multiplica este punto por 32 valores aleatorios. Posteriormente, toma la suma de estos valores aleatorios para derivar una clave de AES y cifrar la flag. A nosotros nos dan el resultado de multiplicar todos los valores aleatorios por , pero no los valores aleatorios ni siquiera .

Parámetros de la curva

Estamos en una situación bastante limitada, ya que no tenemos casi nada de información de la curva. Sin embargo, disponemos de 32 puntos (coordenadas e ) que sabemos que pertenecen a la curva.

Por tanto, sabemos esto:

Si empleamos dos de los puntos que tenemos, podemos deshacernos del parámetro :

Si hacemos esto con otros dos puntos, tenemos una ecuación similar:

Y ahora podemos multiplicar la primera por y la segunda por para poder eliminar la :

Perfecto, ahora tenemos una ecuación que se cumple y que solo depende de las coordenadas de 4 puntos y de . Podemos usar otros 4 puntos para tener otra ecuación similar:

Si pasamos todos los términos a un lado, tenemos dos valores que son divisibles entre :

Entonces, podemos usar el máximo común divisor (GCD) para recuperar (bueno, un múltiplo de , pero podemos quitarle los factores pequeños que tenga).

Una vez que tenemos el módulo sobre el que se opera en la curva, ya es más sencillo encontrar los parámetros y a partir de dos puntos cualesquiera de la curva. Partimos de una expresión anterior:

Como ahora sabemos , podemos calcular inversos respecto al producto, y por tanto, despejar :

Y después de hallar , podemos calcular como

Todo esto se puede implementar con el siguiente código en SageMath:

x, y = [], []
for xx, yy in outputs[:8]:
    x.append(xx)
    y.append(yy)

kN2 = gcd((x[0] - x[1]) * (x[2] ** 3 - x[3] ** 3 - y[2] ** 2 + y[3] ** 2) - (x[2] - x[3]) * (x[0] ** 3 - x[1] ** 3 - y[0] ** 2 + y[1] ** 2), (x[4] - x[5]) * (x[6] ** 3 - x[7] ** 3 - y[6] ** 2 + y[7] ** 2) - (x[6] - x[7]) * (x[4] ** 3 - x[5] ** 3 - y[4] ** 2 + y[5] ** 2))
N2 = kN2

for pp in primes(1000):
    if N2 % pp == 0:
        N2 //= pp

N = isqrt(N2)

print(f'N^2 =', N2)
print(f'N =', N)

a = (y[0] ** 2 - y[1] ** 2 - x[0] ** 3 + x[1] ** 3) * pow(x[0] - x[1], -1, N2) % N2
b = (y[0] ** 2 - x[0] ** 3 - a * x[0]) % N2

print(f'{a = }')
print(f'{b = }')

Y con esto, conseguimos los parámetros de la curva:

$ sage solve_ecc.sage
N^2 = 264565577158994236590031855153889858642149293847448847970649031816068290144718943726237580763969647903770543375415221480423145106277967483944055518720771189157189592025839010707415649298934802554818600881343671391830933519779439364174223387859553464007199819265502917701981157545728448143450273367259289276152361264709006325795000613690279714089006075705019812688622337567736625576157696248463678172321658741121121141186095188499520441835623507334604791145463181077781478470093570533678182144421450743423516076239451209
N = 16265471931640785828934127858946752538285468297743536678369884769134613070708011877740082736319382017849667570641090507172991939418666182470818730451631260930161158328837538561881241462033418605418414010577396121712695567318179840613434951995896817726886735203
a = 255016168931197818685062305277467475939147310316032851940562629263766273806848827361574161304193387338790695002038199730358872156231618756413472252089556793554595535751713490844781606041715667333542594625070573351900213140641050218811210932150487739254199296509019565794946174873502371514562154033669982225110484375322837401197720028302647760803541964996213018205876600519059980832702437327295820859281072782162433368802258604600450884470883303464689592355860840174477238043947992440101763465668785090298241602420559775
b = 50127732115018484203170702229784545965146420529082726037385256846562169633784145549965749115939355046938153878636690046505434313448672070728706649287121339198111456597206969317341833429883720351526802757158855937829665701077162207162706822082172196818620358232889005030349353850169533514493407744045253838278286262204977117355796158321792643972401350420922296278450361220874255243965850220373605475047095584092551599895968561340721051061489824446629675800132597230488528303354169479640856219344579732617565600333600980

Punto generador

Del punto generador sabemos que sus coordenadas e son números de 257 bits, y sabemos que cumple la ecuación de la curva. Además, como el módulo de la curva es , que es un número de bits, si definimos este polinomio:

Tendremos una raíz en , que además es pequeña en comparación con los bits que tiene . Por tanto, podemos usar el método de Coppersmith sobre un polinomio de dos variables para hallar esta raíz pequeña. Para ello, podemos usar la implementación de defund, que admite polinomios de varias variables:

load('coppersmith.sage')
P.<Gx, Gy> = PolynomialRing(Zmod(N2))
f = Gx ** 3 + a * Gx + b - Gy ** 2
roots = small_roots(f, (2 ** 257, 2 ** 257))
Gx, Gy = roots[0]
print(f'{Gx = }')
print(f'{Gy = }')

Y aquí tenemos :

$ sage solve_ecc.sage
N^2 = 264565577158994236590031855153889858642149293847448847970649031816068290144718943726237580763969647903770543375415221480423145106277967483944055518720771189157189592025839010707415649298934802554818600881343671391830933519779439364174223387859553464007199819265502917701981157545728448143450273367259289276152361264709006325795000613690279714089006075705019812688622337567736625576157696248463678172321658741121121141186095188499520441835623507334604791145463181077781478470093570533678182144421450743423516076239451209
N = 16265471931640785828934127858946752538285468297743536678369884769134613070708011877740082736319382017849667570641090507172991939418666182470818730451631260930161158328837538561881241462033418605418414010577396121712695567318179840613434951995896817726886735203
a = 255016168931197818685062305277467475939147310316032851940562629263766273806848827361574161304193387338790695002038199730358872156231618756413472252089556793554595535751713490844781606041715667333542594625070573351900213140641050218811210932150487739254199296509019565794946174873502371514562154033669982225110484375322837401197720028302647760803541964996213018205876600519059980832702437327295820859281072782162433368802258604600450884470883303464689592355860840174477238043947992440101763465668785090298241602420559775
b = 50127732115018484203170702229784545965146420529082726037385256846562169633784145549965749115939355046938153878636690046505434313448672070728706649287121339198111456597206969317341833429883720351526802757158855937829665701077162207162706822082172196818620358232889005030349353850169533514493407744045253838278286262204977117355796158321792643972401350420922296278450361220874255243965850220373605475047095584092551599895968561340721051061489824446629675800132597230488528303354169479640856219344579732617565600333600980
Gx = 187542020032288314214490630204741820227829303492195652833504798640124300158900
Gy = 168843703689929435984972726423710110843417547332425176249556408870268071035700

Factorización basada en curva elíptica

Antes de poder resolver el logaritmo discreto que nos dará la clave para descifrar la flag, necesitamos factorizar , ya que para resolver el logaritmo discreto en la curva definida sobre necesitamos resolverlo antes en y en , y luego utilizar el Teorema Chino del Resto (CRT) para juntar ambos resultados.

La factorización de es algo peculiar, ya que es necesario comprender cómo funciona el método de factorización de curva elíptica de Lenstra:

  • Si queremos factorizar un número , definimos una curva elíptica sobre y un punto sobre dicha curva (podemos generar coordenadas e aleatorias, un parámetro aleatorio y después encontrar un parámetro para que el punto esté en la curva)
  • El objetivo es encontrar un par de puntos en los que la suma de ambos no esté bien definida
  • Para sumar dos puntos, es necesario calcular la pendiente de la recta que une estos puntos. Si esta pendiente es vertical, el resultado es el punto en el infinito. Si resulta que el GCD de este valor de pendiente con es mayor que , el punto no está definido. Pero lo importante es que tendremos un factor de

Para aplicar este conocimiento al reto, tenemos que recordar el valor de (master_eye) que cumplía que en la curva definida sobre :

sage: E = EllipticCurve(Zmod(N), [a, b])
sage: EM = EllipticCurve(Zmod(N2), [a, b])
sage:
sage: G = E((Gx, Gy))
sage: m = 1626547193164078582893412785894675253828546829774353667836988476965589408066956214779521399108300576899339435850978322322115885861611495653342922478
....: 0974963093860223870869151381622793452378040102391285088110131930993214655276327069828109098832154854719776594644
sage: m * G
(0 : 1 : 0)
sage:
sage: P = EM(outputs[0])
sage: m * P
...
ZeroDivisionError: Inverse of 16265471931640785828934127858946752538285468297743536678369884769134613070708011877740082736319382017849667570641090507172991939418666182470818730451631260930161158328837538561881241462033418605418414010577396121712695567318179840613434951995896817726886735203 does not exist (characteristic = 264565577158994236590031855153889858642149293847448847970649031816068290144718943726237580763969647903770543375415221480423145106277967483944055518720771189157189592025839010707415649298934802554818600881343671391830933519779439364174223387859553464007199819265502917701981157545728448143450273367259289276152361264709006325795000613690279714089006075705019812688622337567736625576157696248463678172321658741121121141186095188499520441835623507334604791145463181077781478470093570533678182144421450743423516076239451209 = 16265471931640785828934127858946752538285468297743536678369884769134613070708011877740082736319382017849667570641090507172991939418666182470818730451631260930161158328837538561881241462033418605418414010577396121712695567318179840613434951995896817726886735203*16265471931640785828934127858946752538285468297743536678369884769134613070708011877740082736319382017849667570641090507172991939418666182470818730451631260930161158328837538561881241462033418605418414010577396121712695567318179840613434951995896817726886735203)

Vemos que aparecen errores de que el punto no está definido. Todavía aquí no encontramos un factor de , porque el error dice que no existe inverso de en módulo .

Lo que podemos hacer es encontrar algunos factores de usando factordb.com:

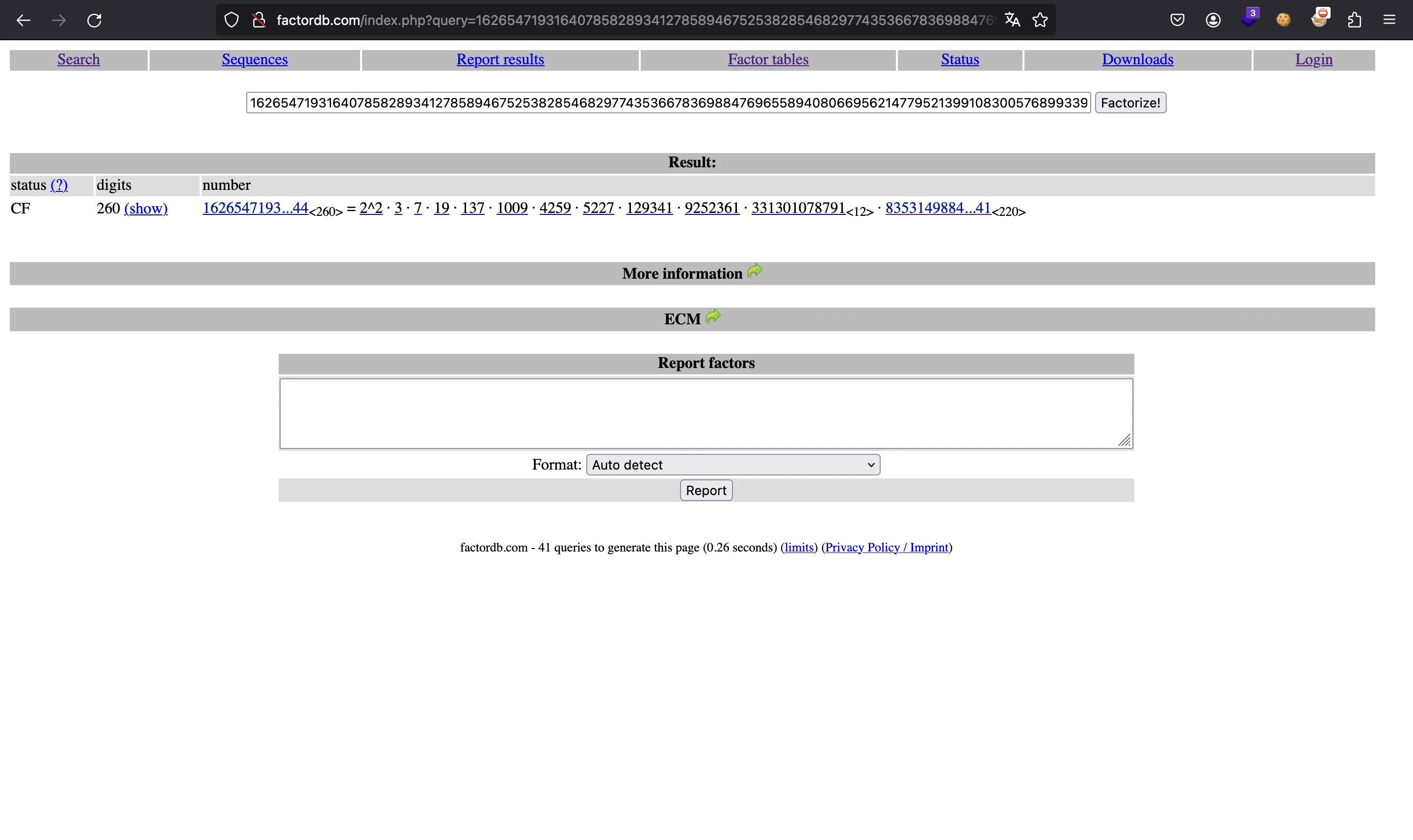
El Reset de 1745 5

Y ahora, en vez de multiplicar por , le quitamos algún factor. Y después de probar un poco, vemos un error algo distinto:

sage: (m // (2 ** 2 * 3)) * P
...
ZeroDivisionError: Inverse of 3306666750998407949290614826810384435005357289027507523518097170844397310630405493724231782674473208511099023446178055658897571567 does not exist (characteristic = 264565577158994236590031855153889858642149293847448847970649031816068290144718943726237580763969647903770543375415221480423145106277967483944055518720771189157189592025839010707415649298934802554818600881343671391830933519779439364174223387859553464007199819265502917701981157545728448143450273367259289276152361264709006325795000613690279714089006075705019812688622337567736625576157696248463678172321658741121121141186095188499520441835623507334604791145463181077781478470093570533678182144421450743423516076239451209 = 3306666750998407949290614826810384435005357289027507523518097170844397310630405493724231782674473208511099023446178055658897571567*80009749116421201819460392082932543369781073296146200526104333277735370142669725871106604546514530470592721417838917956283421712140325370081541030574865070485541235289513992448161233817820635108170971961669125453845627344044069052189301381281546319302677223308512323449970971168044792073413850208786719548578234348518037138428508360825551264023856385886924097308601393744682119824794566727)

Aquí tenemos un factor de :

sage: p = 3306666750998407949290614826810384435005357289027507523518097170844397310630405493724231782674473208511099023446178055658897571567
sage: N % p
0
sage: q = N // p

Logaritmo discreto

El último paso que queda es resolver un logaritmo discreto. El servidor calcula 32 valores aleatorios y los multiplica por en la curva definida sobre :

Luego, utiliza la suma para derivar la clave de AES que cifra la flag.

Una opción es resolver 32 logaritmos discretos y luego sumar los resultados. Sin embargo, parece más eficiente sumar todos los puntos y resolver un solo logaritmo discreto, resultando en , ya que:

Aún así, no es trivial resolver este logaritmo discreto porque estamos en la curva definida sobre . Una curva definida sobre un módulo compuesto se puede descomponer en el “producto” de varias curvas definidas sobre módulos primos (más información en crypto.stackexchange.com). Un reto que puede servir de ejemplo es Ecchimera del CryptoCTF 2021.

Y por otro lado, después de investigar cómo resolver este logaritmo discreto, encontramos un reto llamado “pure division” del zer0pts CTF 2021, y dos writeups que muestran cómo resolverlo:

En este reto, se presenta una curva definida módulo . Para resolverlo, es necesario redefinir la curva sobre (los números -ádicos) con dígitos de precisión. En este cuerpo, el logaritmo discreto es sencillo de resolver porque existe un isomorfismo entre los puntos de la curva y .

Aunque el trasfondo del ataque es altamente complejo, la implementación en SageMath es bastante sencilla. Para nuestro caso, tenemos que poner los puntos de la curva en y , resolver los logaritmos discretos y luego usar el CRT para obtener el resultado en la curva definida sobre :

sage: EM = EllipticCurve(Zmod(N2), [a, b])
sage: G = EM((Gx, Gy))
sage: P = sum(map(EM, outputs))
sage:
sage: Ep_order = EllipticCurve(GF(p), [a, b]).order()
sage:
sage: EQp = EllipticCurve(Qp(p, 2), [a, b])
sage: pG = EQp(G[0] % (p ** 2), G[1] % (p ** 2)) * Ep_order
sage: pP = EQp(P[0] % (p ** 2), P[1] % (p ** 2)) * Ep_order
sage:
sage: sol_p = ZZ((pP[0] / pP[1]) / (pG[0] / pG[1]))
sage: sol_p * pG == pP
True
sage:
sage: Eq_order = EllipticCurve(GF(q), [a, b]).order()
sage:
sage: EQq = EllipticCurve(Qp(q, 2), [a, b])
sage: qG = EQq(G[0] % (q ** 2), G[1] % (q ** 2)) * Eq_order
sage: qP = EQq(P[0] % (q ** 2), P[1] % (q ** 2)) * Eq_order
sage:
sage: sol_q = ZZ((qP[0] / qP[1]) / (qG[0] / qG[1]))
sage: sol_q * qG == qP
True
sage:
sage: sol = crt([sol_p, sol_q], [p, q])
sage: sol * G == P
False

Sin embargo, esta solución no es correcta ya que no se cumple la última igualdad. Pero las igualdades anteriores sí se cumplen.

Lo que está pasando es que esta solución está en módulo , y es el resultado de sumar 32 números menores que . Por tanto, es de esperar que la suma sea algo mayor que , y el resultado que tenemos es menor:

sage: sol < N
True

Entonces, podemos sumarle al resultado hasta que se cumpla la igualdad (serán menos de 32 iteraciones):

sage: while sol * G != P:
....:     sol += N
....:
sage: sol // N
14
sage: sol
228783371310953134200979693682284782082294455467926861967477800951173709471659482447103308284512776967919781995204775749869580375084462240509528430246695076210060525582252947319050463647309271053406795093984733161889288695889919185344579992689803192397436707284

Y ya está. Con este número podemos derivar la clave de AES.

Flag

Finalmente, podemos descifrar la flag con AES:

$ python3 -q
>>> from hashlib import sha256
>>> from Crypto.Cipher import AES
>>> from Crypto.Util.Padding import unpad
>>>
>>> key = sha256(b'228783371310953134200979693682284782082294455467926861967477800951173709471659482447103308284512776967919781995204775749869580375084462240509528430246695076210060525582252947319050463647309271053406795093984733161889288695889919185344579992689803192397436707284').digest()
>>>
>>> unpad(AES.new(key, AES.MODE_CBC, b'iseeyou!' * 2).decrypt(ct), 32)
b'HackOn{3r3s_un4_l3y3nd4_d3_l4_cr1pt0_y_s1nc3r4m3nt3_b4st4nt3_r3pt1li4n0}'