Calibrator
6 minutos de lectura
Se nos proporciona una instancia remota a la que conectarnos:
$ nc 165.227.224.40 31139
[OK] Memory check
[OK] Syncing filesystem
[OK] Detecting sensors
[OK] Module loader
[OK] Reading configurations
Inititing calibration process ...
┌──────────────────────────────────────────────────────────────────────┐
│┼───────────────────┼────────────────────────┼┼──────────────────────┼│
││ XenoCal 2000 │ . ││ ││
│┼───────────────────┤ ┌─┐ x││ . . ││
││ Iteration: 42 │ x ► └─┘ ││ x ││
│┼─────────┬─────────┤ ││ ││
││ X:1337 │ Y:65189 │ . x ┌───┼┼───┐ ││
│┼─────────┴─────────┘ x ┌─┘ ││ └─┐ x ││
││ . ┌─┘ ││ └─┐ ││
││ ┌─┐ x ▼ ┌┘ . ││ └┐ x ││
││ └─┘ . ┌┘ ││ └┐ ││
││ . │ ││ . │ ││
│┼──────────────────────────────────┼─────────┼┼─────────┼────────────┼│
││ x │ x ││ │ ▼ ││
││ x ──►x └┐ ││ ┌┘ ││
││ . ▼ └┐ ││ ┌┘ . ││
││ . └─┐ ││ ┌─┘ ││
││ ┌─┐ x └─┐ ││ ┌─┘ x ││
││ └─┘ ┌─┐ ┌─┐ └───┼┼───┘ ││
││ └─┘ └─┘ ││ ││
││ x . . ││ . ││
││ . x ││ x ││
││ x ▼ x . ││ x ││
││ ││ ││
│┼────────────────────────────────────────────┼┼──────────────────────┼│
└──────────────────────────────────────────────────────────────────────┘ ┌─
│
┌─┬───────────────────────────┬─┐ ┌──────┐ ┌───┼┐
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ │[=()=]│ ├────┤
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ ┌──┼──────┼──┐ │ │
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ │◄├┼┼┼┼┼┼┼┼┤►│ │ │
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ └──┼──────┼──┘ ├────┤
└─┴───────────────────────────┴─┘ │[=()=]│ └────┘
└──────┘
Iteration 0:
>
Análisis de código fuente
Y también tenemos el código fuente en Python:
from FLAG import flag
import random
import math
import time
ITERATIONS = 47
SIDE_LENGTH = 2 * 10 ** 9
ATTEMPTS = 300
HI = SIDE_LENGTH // 2
LO = -SIDE_LENGTH // 2
def banner():
banner = """
┌──────────────────────────────────────────────────────────────────────┐
│┼───────────────────┼────────────────────────┼┼──────────────────────┼│
││ XenoCal 2000 │ . ││ ││
│┼───────────────────┤ ┌─┐ x││ . . ││
││ Iteration: 42 │ x ► └─┘ ││ x ││
│┼─────────┬─────────┤ ││ ││
││ X:1337 │ Y:65189 │ . x ┌───┼┼───┐ ││
│┼─────────┴─────────┘ x ┌─┘ ││ └─┐ x ││
││ . ┌─┘ ││ └─┐ ││
││ ┌─┐ x ▼ ┌┘ . ││ └┐ x ││
││ └─┘ . ┌┘ ││ └┐ ││
││ . │ ││ . │ ││
│┼──────────────────────────────────┼─────────┼┼─────────┼────────────┼│
││ x │ x ││ │ ▼ ││
││ x ──►x └┐ ││ ┌┘ ││
││ . ▼ └┐ ││ ┌┘ . ││
││ . └─┐ ││ ┌─┘ ││
││ ┌─┐ x └─┐ ││ ┌─┘ x ││
││ └─┘ ┌─┐ ┌─┐ └───┼┼───┘ ││
││ └─┘ └─┘ ││ ││
││ x . . ││ . ││
││ . x ││ x ││
││ x ▼ x . ││ x ││
││ ││ ││
│┼────────────────────────────────────────────┼┼──────────────────────┼│
└──────────────────────────────────────────────────────────────────────┘ ┌─
│
┌─┬───────────────────────────┬─┐ ┌──────┐ ┌───┼┐
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ │[=()=]│ ├────┤
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ ┌──┼──────┼──┐ │ │
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ │◄├┼┼┼┼┼┼┼┼┤►│ │ │
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ └──┼──────┼──┘ ├────┤
└─┴───────────────────────────┴─┘ │[=()=]│ └────┘
└──────┘
"""
print(banner)
def load():
boot_messages = \
"""
[\033[92mOK\033[0m] Memory check
[\033[92mOK\033[0m] Syncing filesystem
[\033[92mOK\033[0m] Detecting sensors
[\033[92mOK\033[0m] Module loader
[\033[92mOK\033[0m] Reading configurations
Inititing calibration process ...
""".split('\n')
for m in boot_messages:
print(m)
time.sleep(random.random())
# Calibrator's error acceptance threshold
e = 2
if __name__ == '__main__':
load()
banner()
for i in range(ITERATIONS):
print(f"Iteration {i}:")
R = random.randint(SIDE_LENGTH // 4, SIDE_LENGTH // 2)
X = random.randint(LO + R, HI - R)
Y = random.randint(LO + R, HI - R)
for a in range(ATTEMPTS):
line = input("> ")
x, y = [int(n) for n in line.split(' ')]
D = math.sqrt((X - x) ** 2 + (Y - y) ** 2)
if D <= e:
print("\033[94mREFERENCE", end="\n\033[0m")
break
elif D <= R:
print("\033[92mDETECTED", end="\n\033[0m")
else:
print("\033[91mUNDETECTED", end="\n\033[0m")
else:
exit(0)
print(flag)
El reto ejecuta 47 iteraciones, y en cada iteración, se nos dan 300 intentos de ingresar un punto for-else en Python. El bloque else se ejecuta cuando el bucle for termina (más información en www.w3schools.com), pero no si sale con un break.
Entonces, mirando nuevamente el código de reto, debemos entrar en la declaración if donde D <= e, para que se ejecute break y el servidor no llame a exit(0).
Dibujando el problema
En cada iteración, debemos introducir en un punto LO, HI y SIDE_LENGTH).
Para pasar la iteración, debemos calcular un punto DETECTED. Y si UNDETECTED.
La siguiente figura muestra todas estas secciones:
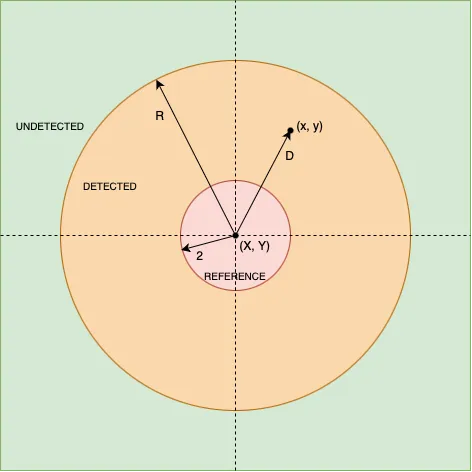
Tenga en cuenta que no conocemos ninguno valor de DETECTED, UNDETECTED para encontrar de alguna manera un punto REFERENCE.
Búsqueda binaria
Como solo tenemos 300 intentos, debemos encontrar un algoritmo de búsqueda rápido que nos permita encontrar un punto REFERENCE. Ya que tenemos un oráculo “binario” (DETECTED o UNDETECTED), intentaremos encontrar una manera de aplicar búsqueda binaria.
El objetivo es encontrar 0 hasta HI), de forma que
Entonces, haremos otra búsqueda binaria en el punto LO hasta 0), tal que
Análogamente, los otros dos algoritmos de búsqueda binaria generarán
Por lo tanto, podemos construir este sistema de ecuaciones:
Restando las dos primeras ecuaciones y las dos últimas, tenemos este sistema de ecuaciones reducido:
Entonces, podemos despejar
Una vez que sepamos el punto
Flag
Después de programar el procedimiento anterior, ejecutamos el script y eventualmente encontramos la flag:
$ python3 solve.py 165.227.224.40:31139
[+] Opening connection to 165.227.224.40 on port 31139: Done
[+] Round: Done
[+] HTB{b1n4ry_s34rch_15_und3rr4t3d}
[*] Closed connection to 165.227.224.40 port 31139
El script completo se puede encontrar aquí: solve.py.