AESWCM
7 minutos de lectura
Se nos proporciona el código fuente del servidor en Python:
from Crypto.Util.Padding import pad
from Crypto.Cipher import AES
import os
import random
from secret import FLAG
KEY = os.urandom(16)
IV = os.urandom(16)
class AESWCM:
def __init__(self, key):
self.key = key
self.cipher = AES.new(self.key, AES.MODE_ECB)
self.BLOCK_SIZE = 16
def pad(self, pt):
if len(pt) % self.BLOCK_SIZE != 0:
pt = pad(pt, self.BLOCK_SIZE)
return pt
def blockify(self, message):
return [
message[i:i + self.BLOCK_SIZE]
for i in range(0, len(message), self.BLOCK_SIZE)
]
def xor(self, a, b):
return bytes([aa ^ bb for aa, bb in zip(a, b)])
def encrypt(self, pt, iv):
pt = self.pad(pt)
blocks = self.blockify(pt)
xor_block = iv
ct = []
for block in blocks:
ct_block = self.cipher.encrypt(self.xor(block, xor_block))
xor_block = self.xor(block, ct_block)
ct.append(ct_block)
return b"".join(ct).hex()
def decrypt(self, ct, iv):
ct = bytes.fromhex(ct)
blocks = self.blockify(ct)
xor_block = iv
pt = []
for block in blocks:
pt_block = self.xor(self.cipher.decrypt(block), xor_block)
xor_block = self.xor(block, pt_block)
pt.append(pt_block)
return b"".join(pt)
def tag(self, pt, iv=os.urandom(16)):
blocks = self.blockify(bytes.fromhex(self.encrypt(pt, iv)))
random.shuffle(blocks)
ct = blocks[0]
for i in range(1, len(blocks)):
ct = self.xor(blocks[i], ct)
return ct.hex()
def main():
aes = AESWCM(KEY)
tags = []
characteristics = []
print("What properties should your magic wand have?")
message = "Property: "
counter = 0
while counter < 3:
characteristic = bytes.fromhex(input(message))
if characteristic not in characteristics:
characteristics.append(characteristic)
characteristic_tag = aes.tag(message.encode() + characteristic, IV)
tags.append(characteristic_tag)
print(characteristic_tag)
if len(tags) > len(set(tags)):
print(FLAG)
counter += 1
else:
print("Only different properties are allowed!")
exit(1)
if __name__ == "__main__":
main()
Análisis del código fuente
En primer lugar, el programa inicializa las variables KEY e IV a 16 bytes aleatorios. Después de eso, se crea una instancia de clase AESWCM.
Luego, se nos pide que ingresemos un mensaje que se etiquetará. Nuestro mensaje (characteristic) se agregará a la lista de mensajes (characteristics). Y la etiqueta (tag) se agregará a la lista de etiquetas (tags).
Veremos la flag cuando len(tags) > len(set(tags)); es decir, cuando haya un elemento repetido en tags (porque no hay elementos duplicados en un set).
El siguiente código refleja la explicación anterior:
message = "Property: "
counter = 0
while counter < 3:
characteristic = bytes.fromhex(input(message))
if characteristic not in characteristics:
characteristics.append(characteristic)
characteristic_tag = aes.tag(message.encode() + characteristic, IV)
tags.append(characteristic_tag)
print(characteristic_tag)
if len(tags) > len(set(tags)):
print(FLAG)
counter += 1
else:
print("Only different properties are allowed!")
exit(1)
Análisis del algoritmo de cifrado
La forma de etiquetar un mensaje (characteristic) es llamando al método tag e ingresando message.encode() + characteristic (es decir, "Property: " concatenado con nuestros datos de entrada).
Este es el método tag:
def tag(self, pt, iv=os.urandom(16)):
blocks = self.blockify(bytes.fromhex(self.encrypt(pt, iv)))
random.shuffle(blocks)
ct = blocks[0]
for i in range(1, len(blocks)):
ct = self.xor(blocks[i], ct)
return ct.hex()
Lo que hace es: encripta el texto plano usando el método encrypt, divide el resultado en bloques de 16 bytes usando blockify y finalmente, baraja los bloques y aplica XOR a todos ellos.
Aquí podemos ver que el shuffle es inútil, porque la operación XOR es conmutativa, el orden no importa.
Uso de AES y XOR
Este es el método encrypt:
def encrypt(self, pt, iv):
pt = self.pad(pt)
blocks = self.blockify(pt)
xor_block = iv
ct = []
for block in blocks:
ct_block = self.cipher.encrypt(self.xor(block, xor_block))
xor_block = self.xor(block, ct_block)
ct.append(ct_block)
return b"".join(ct).hex()
Primero, rellena el mensaje para que su longitud sea un múltiplo de 16 (el tamaño del bloque). Después de eso, lo divide en bloques de 16 bytes y realiza el cifrado.
Recordemos que el cifrado es AES ECB:
class AESWCM:
def __init__(self, key):
self.key = key
self.cipher = AES.new(self.key, AES.MODE_ECB)
self.BLOCK_SIZE = 16
Sin embargo, la función encrypt es bastante similar al modo AES CBC, pero no exactamente igual. A continuación, puede ver cómo es el cifrado AES CBC:
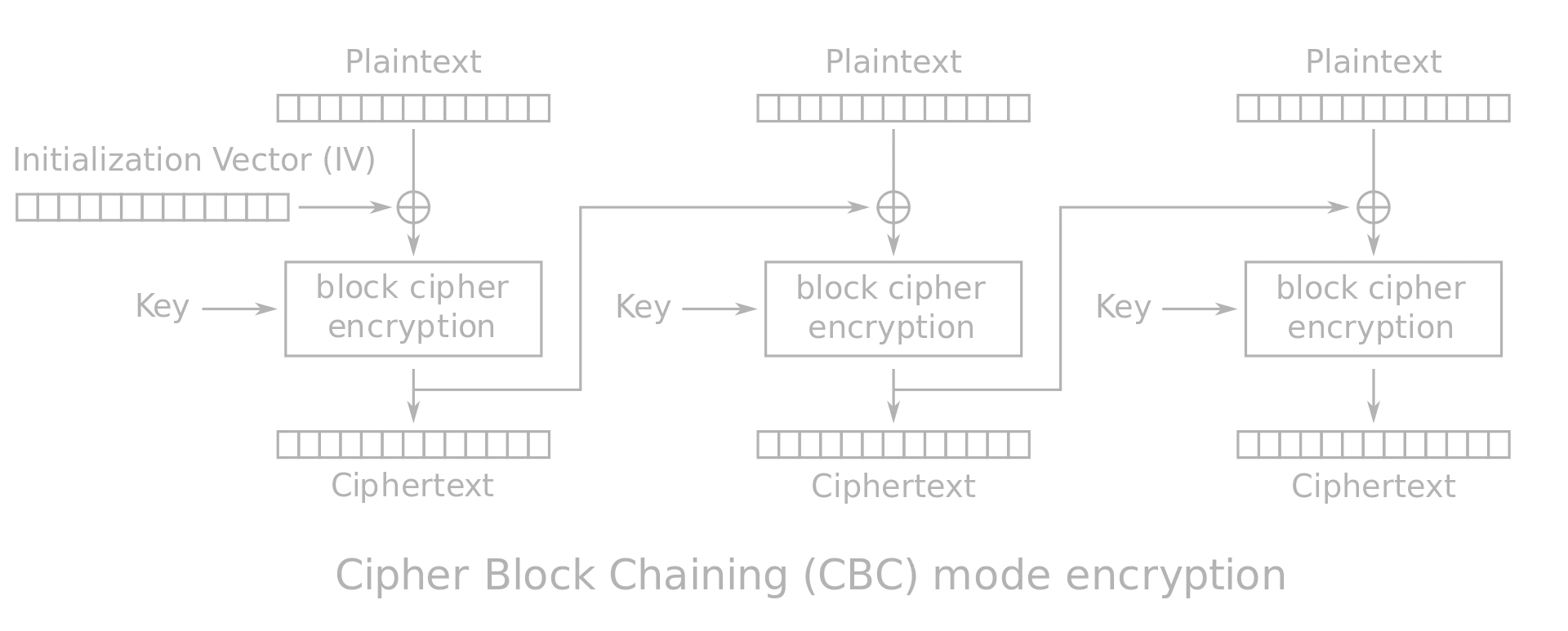
Esta vez, las realimentaciones de cada bloque al siguiente no son los bloques de texto cifrado, sino un XOR entre los bloques de texto cifrado con los bloques de mensaje. Digamos que tenemos 3 bloques de mensaje (
Implementación del relleno
Se necesita relleno para AES porque todos los bloques deben tener 16 bytes. Por lo tanto, la longitud del mensaje debe ser un múltiplo de 16. El método self.pad es este:
def pad(self, pt):
if len(pt) % self.BLOCK_SIZE != 0:
pt = pad(pt, self.BLOCK_SIZE)
return pt
Básicamente, si la longitud del mensaje no es divisible por 16, llama a pad (de Crypto.Util.Padding, que aplica al relleno PKCS7).
Aquí tenemos una configuración errónea. El relleno PKCS7 (si se aplica) debe aplicarse a todos los mensajes, independientemente de si es múltiplo de 16 o no. Y está programado así:
$ python3 -q
>>> from Crypto.Util.Padding import pad
>>> pad(b'A' * 16, 16)
b'AAAAAAAAAAAAAAAA\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10'
>>> pad(b'A' * 32, 16)
b'AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10'
El relleno PKCS7 solo toma el número de bytes restantes y establece ese número como el byte de relleno (digamos que necesitamos 3 bytes más para llegar a un múltiplo de 16, el relleno será "\x03\x03\x03"). En la salida anterior, ya tenemos un texto plano con un tamaño divisible por 16, y aún así pad agrega 16 bytes "\x10 como relleno.
Abusar de la implementación incorrecta
Recordemos que veremos la flag cuando ingresemos dos mensajes diferentes (characteristic) y las salidas sean iguales (tag), de modo que la longitud de la lista es mayor que la longitud del conjunto.
Para hacerlo, podemos ingresar un mensaje en blanco (que estará rellenado) y luego ingresar un relleno falso. Por ejemplo:
>>> def wrong_pad(pt):
... if len(pt) % 16 != 0:
... return pad(pt, 16)
... return pt
...
>>> wrong_pad(b'Property: ' + b'')
b'Property: \x06\x06\x06\x06\x06\x06'
>>> wrong_pad(b'Property: ' + b'\x06\x06\x06\x06\x06\x06')
b'Property: \x06\x06\x06\x06\x06\x06'
Eso es todo: dos mensajes diferentes, el mismo mensaje rellenado; y por lo tanto, el mismo cifrado (tag).
Flag
Para ingresar el mensaje, debemos hacerlo en formato hexadecimal:
$ nc 178.62.21.211 32535
What properties should your magic wand have?
Property:
aed8fd6e4d0b9210ddaccffbf63ed737
Property: 060606060606
aed8fd6e4d0b9210ddaccffbf63ed737
HTB{435_cu570m_m0d35_4nd_hm4c_423_fun!}
Solución intencionada
Para la solución intencionada, evitaremos el relleno ingresando mensajes usando un tamaño múltiplo de 16 bytes. Sea
Para la primera ronda pondremos un solo bloque, y tendremos
.
Entonces estableceremos:
De forma que
.
Obsérvese que
Entonces podemos simplificar
Finalmente, pondremos
Y entonces tendremos que
Nótese que
Y por otro lado,
Por lo tanto,
Como
Implementación en Python
def main():
io = get_process()
p_1_1 = b'Property: ' + bytes.fromhex('00' * 6)
io.sendlineafter(b'Property: ', p_1_1[10:].hex().encode())
e_1 = c_1_1 = bytes.fromhex(io.recvline().decode())
p_2_1 = p_1_1
p_2_2 = xor(e_1, p_1_1)
io.sendlineafter(b'Property: ', (p_2_1 + p_2_2)[10:].hex().encode())
e_2 = bytes.fromhex(io.recvline().decode())
c_2_1 = c_1_1
c_2_2 = xor(e_2, c_2_1)
p_3_1 = p_2_1
p_3_2 = p_2_2
p_3_3 = xor(p_2_2, c_2_2)
io.sendlineafter(b'Property: ', (p_3_1 + p_3_2 + p_3_3)[10:].hex().encode())
io.recvline()
log.success(f'Flag: {io.recvline()}')
io.close()
$ python3 solve.py 178.62.21.211:32535
[+] Opening connection to 178.62.21.211 on port 32535: Done
[+] Flag: b'HTB{435_cu570m_m0d35_4nd_hm4c_423_fun!}'
[*] Closed connection to 178.62.21.211 port 32535
El script completo se puede encontrar aquí: solve.py.