<- HTB UNICTF

Clutch

22 minutos de lectura

Se nos proporciona el siguiente código en Python que implementa un algoritmo cuántico de distribución clave:

from hashlib import sha256
from random import uniform
import json

from Crypto.Util.Padding import unpad
from Crypto.Cipher import AES

from secret import SECRET_MESSAGE
from alice import Alice
from bob import Bob

def json_print(message):
    print(json.dumps(message))

# Python implementation of the Frame-based QKD protocol described here : https://www.mdpi.com/2073-8994/12/6/1053
class QKD:
    # ...


def main():
    json_print({"info": "To all ships of The Frontier Board, use your secret key to get the coordinates of The Starry Spurr"})
    
    json_print({"info": "Initializing QKD..."})

    while True:
        qkd = QKD(Alice, Bob)
        public = qkd.execute()
        
        json_print(public)

        if "error" not in public:
            status = qkd.check_status()
            json_print(status)
            break

    json_print({"info": "Initialization completed. Only trusted ships can send valid commands"})

    while True:
        try:
            data = json.loads(input("> "))
            encrypted_command = bytes.fromhex(data["command"])
            assert len(encrypted_command) % 16 == 0
        except:
            json_print({"error": "Invalid input. Please, try again"})
            continue

        command = qkd.decrypt_command(encrypted_command)
        
        if command == "OPEN THE GATE":
            FLAG = open('flag.txt').read()
            json_print({"info": f" Welcome to The Frontier Board, the coordinates of The Starry Spurr are {SECRET_MESSAGE}{FLAG}"})  
            exit()

        else:
            json_print({"error": "Unknown command. Please, try again"})


if __name__ == '__main__':
    main()

El proyecto está formado por cuatro archivos:

  • server.py
  • alice.py
  • bob.py
  • helpers.py

Hay un enlace a un artículo científico que presenta el algoritmo cuántico que se implementa en Python. Analizaremos el algoritmo y el código.

El algoritmo se conoce como Frame-based Quantum Key Distribution (QKD), y permite que dos partes (Alice y Bob) compartan un secreto de manera segura sobre un canal inseguro usando computación cuántica. En este reto, estamos en la posición de Eve, un usuario malicioso que puede espiar la comunicación entre Alice y Bob, y necesitaremos encontrar el secreto compartido entre ellos, que debería ser difícil de encontrar desde la posición de Eve.

Por lo tanto, podríamos pensar que el algoritmo de QKD es correcto y la implementación de Python tiene un error que nos permite extraer información sensible. Pero también es posible que el algoritmo de QKD no sea completamente seguro, aunque esté publicado en una revista de investigación, y entonces necesitemos encontrar un fallo para obtener el secreto compartido.

Contexto

Para resolver este reto es necesario tener ciertas nociones sobre computación cuántica. Probablemente, todavía no esté preparado para escribir sobre estos conceptos cuánticos de manera rigurosa aquí, pero trataré de explicar los más relevantes:

  • En computación cuántica, los qbit no tienen un valor concreto, tienen un estado de superposición. Esto significa que pueden tener cualquier valor, hasta que se mida el qbit. Una vez que se observa un qbit, colapsa a un valor (0 o 1) y no se puede cambiar. Y esto sucede con cierta probabilidad, que puede expresarse como $\ket{\psi} = \alpha \cdot \ket{0} + \beta \cdot \ket{1}$, donde $|\alpha|^2$ y $|\beta|^2$ representar la probabilidad de colapsar a 0 o a 1, por lo que $|\alpha|^2 + |\beta|^2 = 1$

  • Una puerta de Hadamard (H) produce un “cambio de base”:

    • $H \ket{0} = \displaystyle\frac{1}{\sqrt{2}} \big(\ket{0} + \ket{1}\big) \equiv \ket{+}$

    • $H \ket{1} = \displaystyle\frac{1}{\sqrt{2}} \big(\ket{0} - \ket{1}\big) \equiv \ket{-}$

  • Medir un qbit que ha sido transformado por una puerta de Hadamard tiene un 50% de posibilidades de colapsar a 0 y a 1

El paper utiliza la siguiente notación: $\ket{0_\mathrm{Z}}$ y $\ket{1_\mathrm{Z}}$ para qbits polarizados con la base estándar, y $\ket{0_\mathrm{X}}$ y $\ket{1_\mathrm{X}}$ Para qbits polarizados con la base de Hadamard (es decir, aplicar una puerta de Hadamard antes de medir).

Esto significa que si uno mide usando $\mathrm{Z}$, entonces $\ket{0_\mathrm{Z}}$ colapsa a 0 y $\ket{1_\mathrm{Z}}$ colapsa a 1 con una probabilidad del 100%, mientras que si se mide $\ket{0_\mathrm{X}}$ o $\ket{1_\mathrm{X}}$ colapsarán a 0 o a 1 con una probabilidad del 50% exactamente. Lo mismo sucede al revés, cuando se mide con $\mathrm{X}$.

Este algoritmo de QKD se basa principalmente en el uso de qbits no ortogonales. El propósito es que Alice envía un par de qbits que no son ortogonales, elegidos al azar y polarizados con $\mathrm{X}$ y $\mathrm{Z}$, en este orden.De hecho, solo hay 4 posibles pares no ortogonales:

  • $(\ket{0_\mathrm{X}}, \ket{0_\mathrm{Z}})$
  • $(\ket{0_\mathrm{X}}, \ket{1_\mathrm{Z}})$
  • $(\ket{1_\mathrm{X}}, \ket{0_\mathrm{Z}})$
  • $(\ket{1_\mathrm{X}}, \ket{1_\mathrm{Z}})$

Entonces, Bob mide con una base cualquiera entre $\mathrm{Z}$ y $\mathrm{X}$, para que uno de los qbits siempre se mida correctamente. El autor usa el término double matching para referirse al hecho de medir el mismo valor en ambos qbits. Por ejemplo, si Bob recibe $(\ket{0_\mathrm{X}}, \ket{1_\mathrm{Z}})$ y mide con $\mathrm{X}$, Él puede decodificar como $(0, 0)$ o $(0, 1)$. El primero es un double matching, mientras que el segundo no.

Otro concepto a saber antes de sumergirnos en el protocolo de QKD es un frame binario (o simplemente, frame). Esta es simplemente una matriz de pares de qbits no ortogonales. Por ejemplo, los pares $(\ket{1_\mathrm{X}}, \ket{1_\mathrm{Z}})$ y $(\ket{0_\mathrm{X}}, \ket{1_\mathrm{Z}})$ se pueden organizar como

$$ \begin{pmatrix} \ket{1_\mathrm{X}} & \ket{1_\mathrm{Z}} \\ \ket{0_\mathrm{X}} & \ket{1_\mathrm{Z}} \end{pmatrix} $$

El paper muestra en la Tabla 3 que no todos los frames son útiles, solo hay 6 que son útiles para el protocolo de QKD, mientras que algunos de los frames inútiles se pueden usar como frames auxiliares para detección y corrección de errores.

Finalmente, el concepto de matching result es la configuración que resulta de la medición de Bob al obtener un double matching. Por ejemplo, si Bob mide $(\ket{1_\mathrm{X}}, \ket{1_\mathrm{Z}})$ con $\mathrm{Z}$ y obtiene $(1, 1)$, y luego mide $(\ket{0_\mathrm{X}}, \ket{1_\mathrm{Z}})$ con $\mathrm{X}$ y obtiene $(0, 0)$, el matching result se puede representar como

$$ \begin{pmatrix} - & \ket{\bullet_\mathrm{Z}} \\ \ket{\bullet_\mathrm{X}} & - \end{pmatrix} $$

Como Bob obtuvo un matching result al medir el primer par con $\mathrm{X}$ y el segundo par con $\mathrm{Z}$. la Table 4 del paper muestra los 4 configuraciones posibles y los codifica como bits 00, 01, 10, 11 para una decodificación posterior.

QKD basado en frames

Mostraré los pasos del algoritmo y luego haremos un breve ejemplo usando el código fuente:

  1. Alice envía $n$ pares elegidos al azar del conjunto de 4 pares posibles
  2. Bob elige la base para medir cada uno de los $n$ pares, al azar entre $\mathrm{X}$ o $\mathrm{Z}$
  3. Bob dice los índices de los pares que obtuvieron un double matching
  4. Alice toma los índices y realiza combinaciones tomadas de 2 en 2 para formar frames, y descarta los inútiles
  5. Alice envía los frames a Bob como tuplas de índices
  6. Bob calcula las sifting strings (sifting bits y bits medidos) y las envía a Alice
  7. Alice es capaz de obtener los double matchings de Bob y saber la elección de las bases de medición para cada par de qbits
  8. Alice y Bob calculan un secreto compartido en función de las bases de medición de Bob

La Figura 6 del paper muestra el siguiente flujo:

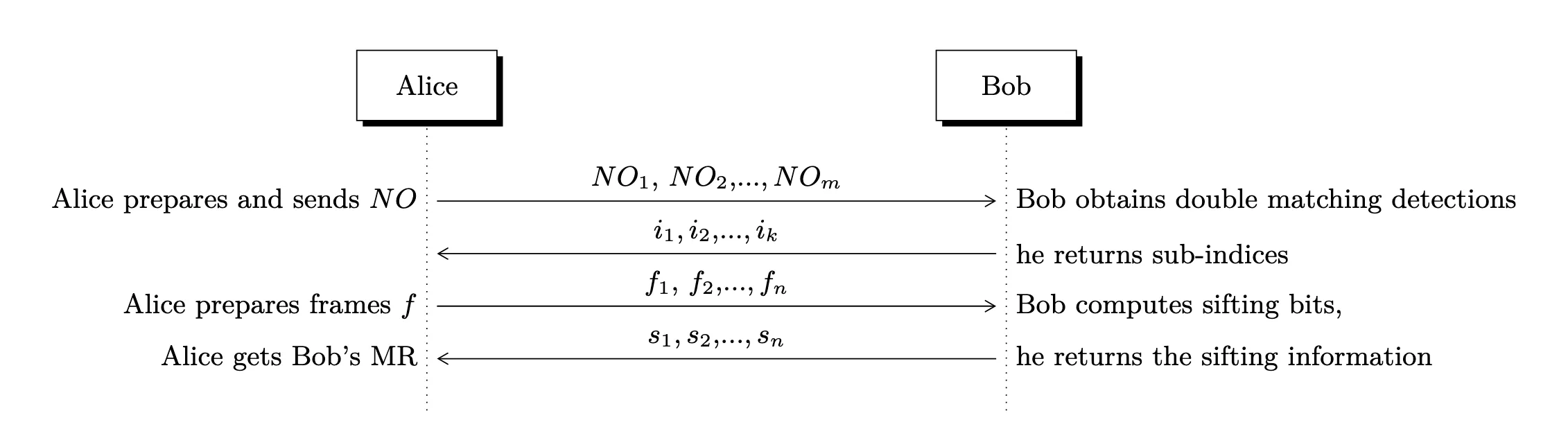
Clutch 5

Hay un paso adicional antes de derivar la clave compartida. Alice debe encontrar frames ambiguos y decirle a Bob qué frames son ambiguos, para que no se usen esos frames.

Análisis del código fuente

El protocolo de nivel superior se puede leer en la clase QKD de server.py:

class QKD:
    def __init__(self, Alice, Bob, pairs = 256, security = 256):
        self.Alice = Alice(pairs)
        self.Bob = Bob(uniform(0, 1))

        self.security = security

    def check_status(self):
        return {"status": "OK", "QBER": self.Bob.depolarizing_probability}

    def execute(self):
        pairs = self.Alice.prepare()
        double_matchings = self.Bob.measure(pairs)

        if not len(double_matchings):
            return {"error": "Key exchange failed, there's no double matchings. Retrying..."}
    
        frames, usable_frames, auxiliary_frames = self.Alice.compute_frames(double_matchings)

        if not len(frames):
            return {"error": "Key exchange failed, there's no frames. Retrying..."}

        bob_sifting_strings = self.Bob.compute_sifting_strings(frames)

        alice_sifting_strings, ambiguous_frames = self.Alice.error_correction(usable_frames, auxiliary_frames, bob_sifting_strings)

        alice_key = self.Alice.generate_shared_key(frames, usable_frames, ambiguous_frames, alice_sifting_strings, bob_sifting_strings)  

        bob_key = self.Bob.generate_shared_key(frames, ambiguous_frames, bob_sifting_strings)

        if len(alice_key) < self.security:
            return {"error": "Key exchange failed, the instance does not satisfy the security requirements. Retrying..."}

        if alice_key != bob_key:
            return {"error": "Key exchange failed, both keys are not equal. Retrying..."}

        bob_sifting_strings = list(bob_sifting_strings.values())

        public = {
            "double_matchings": double_matchings,
            "frames": frames,
            "sifting_strings": bob_sifting_strings,
            "ambiguous_frames": ambiguous_frames
        }

        self.shared_key = alice_key.encode()

        return public

Paso 1: En primer lugar, Alice genera pares de qbits no ortogonales aleatorios (por defecto, un total de 256), y se guardan en pairs_data:

class Alice:
    def __init__(self, pairs):
        self.pairs = pairs
        self.pairs_data = {}
        
        # Setting up global parameters. Local variables with the same name refers to the frames generated in the actual QKD instance  
        self.usable_frames = USABLE_FRAMES
        self.usable_frames_iterable = list(self.usable_frames.keys())

        self.auxiliary_frames = AUXILIARY_FRAMES
        self.auxiliary_frames_iterable = list(self.auxiliary_frames.keys())
        
        self.generate_pairs()
        
    def generate_pairs(self):
        for i in range(self.pairs):
            x, z = [ randbits(1) for _ in range(2) ]
            self.pairs_data[i] = f"{x}x,{z}z"

    def prepare(self):
        pairs = []
        for i in range(self.pairs):
            circuits = self.generate_circuits(self.pairs_data[i])
            pairs.append(circuits)
        return pairs
            
    def generate_circuits(self, pair):
        x, z = [ int(state[0]) for state in pair.split(",") ]
        circuits = [ QuantumCircuit(1, 1) for _ in range(2) ]
        
        if x: circuits[0].x(0)
        if z: circuits[1].x(0)
        
        circuits[0].h(0)
        
        return circuits

El valor de devuelto por Alice.prepare es una lista de circuitos cuánticos que codifican los pares de qbits. Estos circuitos son muy sencillos, solo usan puertas X y H para obtener uno de los 4 pares de qbits no ortogonales posibles. Entonces, nada realmente interesante que ver aquí.

Paso 2: Luego, Bob mide cada circuito utilizando una base aleatoria:

class Bob:
    def __init__(self, depolarizing_probability = 0):
        self.depolarizing_probability = depolarizing_probability
        
        self.measurement_basis = {}
        self.measurement_results = {}
        self.backend = Aer.get_backend("qasm_simulator")

    def noise_model(self, p):
        error_model = depolarizing_error(p, 1)
        
        noise_model = NoiseModel()
        noise_model.add_all_qubit_quantum_error(error_model, "measure")

        return noise_model
        
    def measure(self, pairs):
        double_matchings = []

        noise_model = None
        if self.depolarizing_probability > 0:
            noise_model = self.noise_model(self.depolarizing_probability)
        
        for i in range(len(pairs)):
            basis = randbits(1)
            if basis:
                # Measurement in "X" basis
                pairs[i][0].h(0)
                pairs[i][1].h(0)
                
            pairs[i][0].measure(0, 0)
            pairs[i][1].measure(0, 0)

            bits = ""
            for circuit in pairs[i]:
                transpiled = transpile(circuit, self.backend)
                results = self.backend.run(transpiled, noise_model = noise_model, shots = 1).result().get_counts()  
                bits += list(results.keys())[0]
            
            if bits[0] == bits[1]: double_matchings.append(i)
            
            self.measurement_results[i] = bits
            self.measurement_basis[i] = "X" if basis else "Z"
        
        return double_matchings

Como se puede ver, Bob introduce algo de ruido en los circuitos con una probabilidad de error de despolarización, para hacerlo más realista.

Paso 3: La salida de Bob.measure es la lista de índices que dieron como resultado un double matching. Bob también guarda las medidas en measurements_results y la base escogida en measurement_basis.

Paso 4: Alice calcula frames basados ​​en combinaciones tomadas de 2 en 2 de los índices con double matching:

    def public_frame_to_private_frame(self, frame):
        return (self.pairs_data[frame[0]], self.pairs_data[frame[1]])

    def compute_frames(self, double_matchings):
        usable_frames = {}
        auxiliary_frames = {}
        
        public_frames = list(combinations(double_matchings, 2))

        for public_frame in public_frames:
            private_frame = self.public_frame_to_private_frame(public_frame)

            if private_frame in self.usable_frames_iterable:
                usable_frames[public_frame] = self.usable_frames[private_frame]
            
            elif private_frame in self.auxiliary_frames_iterable:
                auxiliary_frames[public_frame] = self.auxiliary_frames[private_frame]  

        frames = list(usable_frames.keys()) + list(auxiliary_frames.keys())
        
        shuffle(frames)

        return frames, usable_frames, auxiliary_frames

Paso 5: Alice desordena la lista de frames, aunque esto no aumenta la seguridad, en mi opinión. Luego, son enviados a Bob.

Paso 6: Ahora Bob usa compute_sifting_strings para calcular tanto los sifting bits como los bits medidos:

    def compute_sifting_bits(self, frame):
        sifting_bits = {
            "X": 0, 
            "Z": 0
        }
        
        for pair in frame:
            sifting_bits[self.measurement_basis[pair]] ^= int(self.measurement_results[pair][0])
            
        return ''.join(map(str, sifting_bits.values()))

    def compute_measured_bits(self, frame):
        measured_bits = []

        for pair in frame:
            measured_bits.append(self.measurement_results[pair][0]) # since both bits are equal due to the double matching event  

        return ''.join(measured_bits)
            
    def compute_sifting_strings(self, frames):
        sifting_strings = {}

        for frame in frames:
            sifting_bits = self.compute_sifting_bits(frame)
            measured_bits = self.compute_measured_bits(frame)

            sifting_strings[frame] = f"{sifting_bits},{measured_bits}"

        return sifting_strings

Estas sifting strings son realmente interesantes porque dan demasiada información. En primer lugar, los sifting bits son el XOR de las columnas de los pares medidos, considerando solo los valores que son 100% correctos, y el resto como 0. Por ejemplo,

$$ \text{Alice:} \begin{pmatrix} \ket{1_\mathrm{X}} & \ket{1_\mathrm{Z}} \\ \ket{0_\mathrm{X}} & \ket{1_\mathrm{Z}} \end{pmatrix} \longrightarrow \text{Bob:} \begin{Bmatrix} \mathrm{Z}\\ \mathrm{X} \end{Bmatrix} \longrightarrow \begin{pmatrix} - & \ket{1_\mathrm{Z}} \\ \ket{0_\mathrm{X}} & - \end{pmatrix} \longrightarrow \text{01} $$

Por otro lado, los bits medidos son simplemente $10$, en orden de fila. Dado que ambos pares son double matchings, el signo $-$ no es relevante. Entonces, la sifting string en este ejemplo es 01,10.

Paso 7: Alice realiza la detección y corrección de errores en las sifting string de Bob:

    def verify_undetected_error(self, pair, detection_frame, required_sifting_string, frame, auxiliary_frames, auxiliary_frames_iterable, sifting_string):  
        for auxiliary_frame in auxiliary_frames_iterable:
            if  (
                    frame[pair]                       == auxiliary_frame[0]      and 
                    auxiliary_frames[auxiliary_frame] == detection_frame         and 
                    sifting_string[auxiliary_frame]   == required_sifting_string
                ):

                return True

        return False
    
    def error_correction(self, usable_frames, auxiliary_frames, bob_sifting_strings):
        alice_sifting_strings = bob_sifting_strings.copy()
        
        ambiguous_frames = []

        usable_frames_iterable = list(usable_frames.keys())
        auxiliary_frames_iterable = list(auxiliary_frames.keys())

        for frame in usable_frames_iterable:
            if alice_sifting_strings[frame] in VALID_SS[usable_frames[frame]]:
                sifting_bits = alice_sifting_strings[frame][:2]

                if sifting_bits == "01" or sifting_bits == "10":
                    ambiguous_frames.append(frame)

                else:
                    pair, detection_frame, required_sifting_string, corrections = ERROR_CORRECTION_RULES[usable_frames[frame]]
                    
                    verify = self.verify_undetected_error(
                                pair, 
                                detection_frame, 
                                required_sifting_string, 
                                frame, 
                                auxiliary_frames,
                                auxiliary_frames_iterable, 
                                alice_sifting_strings
                            )

                    if verify:
                        if  alice_sifting_strings[frame] == "00,11":
                            alice_sifting_strings[frame] = corrections[0]
                            
                        elif alice_sifting_strings[frame] == "11,11":
                             alice_sifting_strings[frame] = corrections[1]

            else:
                ambiguous_frames.append(frame)

        ambiguous_frames += auxiliary_frames

        shuffle(ambiguous_frames)
        
        return alice_sifting_strings, ambiguous_frames

Este proceso está dedicado a descartar frames que resultan ambiguos debido a errores al medir los qbits en los circuitos simulados. Con esto, Alice obtiene las sifting strings correctas, que se pueden usar para calcular el secreto compartido. Bob también necesita conocer los frames que son ambiguos para descartarlos más tarde.

Paso 8: Alice y Bob pueden generar el mismo secreto:

    def generate_shared_key(self, frames, usable_frames, ambiguous_frames, alice_sifting_strings, bob_sifting_strings):  
        shared_secret = ""

        for frame in frames:
            if frame in ambiguous_frames:
                continue

            else:
                sifting_bits = alice_sifting_strings[frame][:2]
                measurement_result = ALICE_MR_DERIVATION[usable_frames[frame]][sifting_bits]
                shared_secret += KEY_DERIVATION[bob_sifting_strings[frame]][measurement_result]
        
        return shared_secret

    def generate_shared_key(self, frames, ambiguous_frames, sifting_strings):
        shared_secret = ""

        for frame in frames:
            if frame in ambiguous_frames:
                continue

            else:
                basis_orientation = (self.measurement_basis[frame[0]], self.measurement_basis[frame[1]])  
                measurement_result = BOB_MR_DERIVATION[basis_orientation]
                shared_secret += KEY_DERIVATION[sifting_strings[frame]][measurement_result]

        return shared_secret

La forma que tiene Alice de generar el secreto parece más complicada. Por el lado de Bob, solamente toma las bases de medición que calculó al azar y las usa para derivar el secreto usando una tabla que depende de los resultados de la medición.

Solución

Empecé a jugar con Alice y Bob en el REPL de Python, con un tamaño de clave pequeño:

$ python3 -q
>>> from server import Alice, Bob, QKD
>>>
>>> while True:
...     qkd = QKD(Alice, Bob, 16, 8)
...     public = qkd.execute()
...     if 'error' not in public:
...         break
...
>>> public
{'double_matchings': [2, 3, 4, 6, 7, 8, 9, 11, 12, 13, 14, 15], 'frames': [(2, 15), (3, 13), (7, 12), (4, 14), (4, 7), (4, 6), (7, 13), (3, 12), (9, 15), (8, 15), (6, 15), (8, 13), (9, 13), (4, 9), (12, 15), (4, 8), (2, 13), (7, 15), (2, 4), (11, 12), (6, 12), (11, 15), (8, 12), (6, 13), (3, 15), (13, 15), (2, 12), (12, 13), (11, 13), (9, 12), (4, 11), (3, 4), (14, 15)], 'sifting_strings': ['11,11', '01,10', '00,11', '10,10', '11,11', '00,11', '01,10', '00,11', '11,11', '10,01', '00,11', '00,00', '01,10', '11,11', '11,11', '10,10', '01,10', '11,11', '11,11', '11,11', '11,11', '00,11', '01,01', '10,10', '11,11', '10,01', '00,11', '01,10', '10,10', '00,11', '00,11', '11,11', '10,01'], 'ambiguous_frames': [(7, 12), (13, 15), (9, 12), (11, 13), (3, 12), (3, 13), (8, 15), (12, 15), (11, 12), (14, 15), (2, 13), (7, 13), (8, 12), (4, 8), (4, 14), (9, 13), (2, 12), (6, 12), (6, 13), (12, 13), (8, 13)]}  
>>>
>>> double_matchings = public.get('double_matchings')
>>> frames = list(map(tuple, data.get('frames', [])))
>>> sifting_strings = public.get('sifting_strings')
>>> ambiguous_frames = set(map(tuple, public.get('ambiguous_frames', [])))
>>>
>>> double_matchings
[2, 3, 4, 6, 7, 8, 9, 11, 12, 13, 14, 15]
>>> frames
[(2, 15), (3, 13), (7, 12), (4, 14), (4, 7), (4, 6), (7, 13), (3, 12), (9, 15), (8, 15), (6, 15), (8, 13), (9, 13), (4, 9), (12, 15), (4, 8), (2, 13), (7, 15), (2, 4), (11, 12), (6, 12), (11, 15), (8, 12), (6, 13), (3, 15), (13, 15), (2, 12), (12, 13), (11, 13), (9, 12), (4, 11), (3, 4), (14, 15)]
>>> sifting_strings
['11,11', '01,10', '00,11', '10,10', '11,11', '00,11', '01,10', '00,11', '11,11', '10,01', '00,11', '00,00', '01,10', '11,11', '11,11', '10,10', '01,10', '11,11', '11,11', '11,11', '11,11', '00,11', '01,01', '10,10', '11,11', '10,01', '00,11', '01,10', '10,10', '00,11', '00,11', '11,11', '10,01']
>>> ambiguous_frames
{(6, 12), (12, 13), (3, 13), (8, 12), (8, 15), (7, 13), (4, 8), (4, 14), (12, 15), (3, 12), (14, 15), (9, 13), (11, 13), (2, 13), (6, 13), (7, 12), (9, 12), (11, 12), (8, 13), (2, 12), (13, 15)}

Comencemos por ver algunos valores que se supone que no deberíamos saber. Por ejemplo, la variable bob_sifting_strings se obtiene de compute_sifting_strings a partir de frames (pondré un guion bajo inicial para denotar variables privadas):

>>> _bob_sifting_strings = qkd.Bob.compute_sifting_strings(frames)
>>> _bob_sifting_strings
{(2, 15): '11,11', (3, 13): '01,10', (7, 12): '00,11', (4, 14): '10,10', (4, 7): '11,11', (4, 6): '00,11', (7, 13): '01,10', (3, 12): '00,11', (9, 15): '11,11', (8, 15): '10,01', (6, 15): '00,11', (8, 13): '00,00', (9, 13): '01,10', (4, 9): '11,11', (12, 15): '11,11', (4, 8): '10,10', (2, 13): '01,10', (7, 15): '11,11', (2, 4): '11,11', (11, 12): '11,11', (6, 12): '11,11', (11, 15): '00,11', (8, 12): '01,01', (6, 13): '10,10', (3, 15): '11,11', (13, 15): '10,01', (2, 12): '00,11', (12, 13): '01,10', (11, 13): '10,10', (9, 12): '00,11', (4, 11): '00,11', (3, 4): '11,11', (14, 15): '10,01'}

Obsérvese que podemos obtener este valor uniendo frames y sifting_strings:

>>> dict(zip(frames, sifting_strings)) == _bob_sifting_strings  
True
>>> bob_sifting_strings = dict(zip(frames, sifting_strings))

Otra cosa a notar es que la longitud de la clave compartida en bits es igual a la longitud de frames menos la de ambiguous_frames:

>>> _shared_key = qkd.shared_key
>>> _shared_key
b'010001000000'
>>> len(_shared_key)
12
>>> len(frames)
33
>>> len(ambiguous_frames)
21
>>> len(frames) - len(ambiguous_frames) == len(_shared_key)  
True

Sabemos que ningún frame de ambiguous_frames se utiliza para generar el secreto compartido, por lo tanto, podemos encontrar fácilmente los frames que realmente se usan para generar el secreto (que determina la longitud del secreto):

>>> used = sorted(set(frames).difference(ambiguous_frames))
>>> used
[(2, 4), (2, 15), (3, 4), (3, 15), (4, 6), (4, 7), (4, 9), (4, 11), (6, 15), (7, 15), (9, 15), (11, 15)]

Echemos un segundo vistazo a la condición que hace que un frame sea ambiguo o no:

    def error_correction(self, usable_frames, auxiliary_frames, bob_sifting_strings):  
        alice_sifting_strings = bob_sifting_strings.copy()
        
        ambiguous_frames = []

        usable_frames_iterable = list(usable_frames.keys())
        auxiliary_frames_iterable = list(auxiliary_frames.keys())

        for frame in usable_frames_iterable:
            if alice_sifting_strings[frame] in VALID_SS[usable_frames[frame]]:
                sifting_bits = alice_sifting_strings[frame][:2]

                if sifting_bits == "01" or sifting_bits == "10":
                    ambiguous_frames.append(frame)

                else:
                    # ...

            else:
                ambiguous_frames.append(frame)

        ambiguous_frames += auxiliary_frames

        shuffle(ambiguous_frames)
        
        return alice_sifting_strings, ambiguous_frames

¡Podemos ver que los sifting bits $01$ y $10$ son siempre ambiguos! Comprobémoslo:

>>> bob_sifting_strings
{(2, 15): '11,11', (3, 13): '01,10', (7, 12): '00,11', (4, 14): '10,10', (4, 7): '11,11', (4, 6): '00,11', (7, 13): '01,10', (3, 12): '00,11', (9, 15): '11,11', (8, 15): '10,01', (6, 15): '00,11', (8, 13): '00,00', (9, 13): '01,10', (4, 9): '11,11', (12, 15): '11,11', (4, 8): '10,10', (2, 13): '01,10', (7, 15): '11,11', (2, 4): '11,11', (11, 12): '11,11', (6, 12): '11,11', (11, 15): '00,11', (8, 12): '01,01', (6, 13): '10,10', (3, 15): '11,11', (13, 15): '10,01', (2, 12): '00,11', (12, 13): '01,10', (11, 13): '10,10', (9, 12): '00,11', (4, 11): '00,11', (3, 4): '11,11', (14, 15): '10,01'}  
>>> ambiguous_frames
{(6, 12), (12, 13), (3, 13), (8, 12), (8, 15), (7, 13), (4, 8), (4, 14), (12, 15), (3, 12), (14, 15), (9, 13), (11, 13), (2, 13), (6, 13), (7, 12), (9, 12), (11, 12), (8, 13), (2, 12), (13, 15)}
>>> for t, s in bob_sifting_strings.items():
...     print(t, ' \t', repr(s), '\t', t in ambiguous_frames)
...
(2, 15)          '11,11'         False
(3, 13)          '01,10'         True
(7, 12)          '00,11'         True
(4, 14)          '10,10'         True
(4, 7)           '11,11'         False
(4, 6)           '00,11'         False
(7, 13)          '01,10'         True
(3, 12)          '00,11'         True
(9, 15)          '11,11'         False
(8, 15)          '10,01'         True
(6, 15)          '00,11'         False
(8, 13)          '00,00'         True
(9, 13)          '01,10'         True
(4, 9)           '11,11'         False
(12, 15)         '11,11'         True
(4, 8)           '10,10'         True
(2, 13)          '01,10'         True
(7, 15)          '11,11'         False
(2, 4)           '11,11'         False
(11, 12)         '11,11'         True
(6, 12)          '11,11'         True
(11, 15)         '00,11'         False
(8, 12)          '01,01'         True
(6, 13)          '10,10'         True
(3, 15)          '11,11'         False
(13, 15)         '10,01'         True
(2, 12)          '00,11'         True
(12, 13)         '01,10'         True
(11, 13)         '10,10'         True
(9, 12)          '00,11'         True
(4, 11)          '00,11'         False
(3, 4)           '11,11'         False
(14, 15)         '10,01'         True

Se ve correcto, todas las sifting strings que comienzan con 01 oo 10 son ambiguoas. Por lo tanto, estos son los frames no ambiguos:

>>> non_ambiguous = {t: s for t, s in bob_sifting_strings.items() if s[:2] in {'00', '11'}}
>>> non_ambiguous
{(2, 15): '11,11', (7, 12): '00,11', (4, 7): '11,11', (4, 6): '00,11', (3, 12): '00,11', (9, 15): '11,11', (6, 15): '00,11', (8, 13): '00,00', (4, 9): '11,11', (12, 15): '11,11', (7, 15): '11,11', (2, 4): '11,11', (11, 12): '11,11', (6, 12): '11,11', (11, 15): '00,11', (3, 15): '11,11', (2, 12): '00,11', (9, 12): '00,11', (4, 11): '00,11', (3, 4): '11,11'}

Sin embargo, necesitamos tomar los frames que se usaron realmente:

>>> used_non_ambiguous = {t: s for t, s in non_ambiguous.items() if t in used}
>>> used_non_ambiguous
{(2, 15): '11,11', (4, 7): '11,11', (4, 6): '00,11', (9, 15): '11,11', (6, 15): '00,11', (4, 9): '11,11', (7, 15): '11,11', (2, 4): '11,11', (11, 15): '00,11', (3, 15): '11,11', (4, 11): '00,11', (3, 4): '11,11'}  
>>>
>>> for t, s in used_non_ambiguous.items():
...     print(t, ' \t', repr(s))
...
(2, 15)          '11,11'
(4, 7)           '11,11'
(4, 6)           '00,11'
(9, 15)          '11,11'
(6, 15)          '00,11'
(4, 9)           '11,11'
(7, 15)          '11,11'
(2, 4)           '11,11'
(11, 15)         '00,11'
(3, 15)          '11,11'
(4, 11)          '00,11'
(3, 4)           '11,11'

Esto es muy interesante. Todas las sifting strings usadas son 00,11 o 11,11… Echemos un vistazo a las bases de medición de Bob:

>>> for i, b in qkd.Bob.measurement_basis.items():  
...     print(f'{i:2d}: {b}')
...
 0: Z
 1: Z
 2: Z
 3: Z
 4: X
 5: Z
 6: X
 7: Z
 8: Z
 9: Z
10: X
11: X
12: Z
13: Z
14: X
15: X

¿Notas algo raro? Combinemos las salidas:

>>> for t, s in used_non_ambiguous.items():
...     print(t, ' \t', repr(s), '\t', (_basis[t[0]], _basis[t[1]]))  
...
(2, 15)          '11,11'         ('Z', 'X')
(4, 7)           '11,11'         ('X', 'Z')
(4, 6)           '00,11'         ('X', 'X')
(9, 15)          '11,11'         ('Z', 'X')
(6, 15)          '00,11'         ('X', 'X')
(4, 9)           '11,11'         ('X', 'Z')
(7, 15)          '11,11'         ('Z', 'X')
(2, 4)           '11,11'         ('Z', 'X')
(11, 15)         '00,11'         ('X', 'X')
(3, 15)          '11,11'         ('Z', 'X')
(4, 11)          '00,11'         ('X', 'X')
(3, 4)           '11,11'         ('Z', 'X')

¡Eh! Si una sifting string es 11,11, entonces las bases de medición son $(\mathrm{Z}, \mathrm{X})$ o $(\mathrm{X}, \mathrm{Z})$. Por otro lado, si la sifting string is 00,11, entonces las bases son $(\mathrm{Z}, \mathrm{Z})$ oo $(\mathrm{X}, \mathrm{X})$.

Con esta información, simplemente podemos elegir una base inicial para un índice y luego derivar el resto utilizando las condiciones anteriores. Podemos hacer esto con un algoritmo sencillo:

basis = {used[0][0]: 'X'}

while len(basis) < len(used):
    old_basis = basis.copy()

    for u, m in old_basis.items():
        for t, v in used_non_ambiguous.items():
            if u == t[0] and v == '11,11' and t[1] not in basis:
                basis[t[1]] = 'Z' if m == 'X' else 'X'
            elif u == t[1] and v == '11,11' and t[0] not in basis:  
                basis[t[0]] = 'Z' if m == 'X' else 'X'
            elif u == t[0] and v == '00,11' and t[1] not in basis:
                basis[t[1]] = m
            elif u == t[1] and v == '00,11' and t[0] not in basis:
                basis[t[0]] = m

    if len(old_basis) == len(basis):
        break

Tendremos un 50% de probabilidad de obtener la base correcta:

>>> basis = {used[0][0]: 'X'}
>>>
>>> while len(basis) < len(used):
...     old_basis = basis.copy()
...     for u, m in old_basis.items():
...         for t, v in used_non_ambiguous.items():
...             if u == t[0] and v == '11,11' and t[1] not in basis:
...                 basis[t[1]] = 'Z' if m == 'X' else 'X'
...             elif u == t[1] and v == '11,11' and t[0] not in basis:
...                 basis[t[0]] = 'Z' if m == 'X' else 'X'
...             elif u == t[0] and v == '00,11' and t[1] not in basis:
...                 basis[t[1]] = m
...             elif u == t[1] and v == '00,11' and t[0] not in basis:
...                 basis[t[0]] = m
...     if len(old_basis) == len(basis):
...         break
...
>>> basis_x = basis
>>> basis_x
{2: 'X', 15: 'Z', 4: 'Z', 9: 'X', 6: 'Z', 7: 'X', 11: 'Z', 3: 'X'}
>>> _basis
{0: 'Z', 1: 'Z', 2: 'Z', 3: 'Z', 4: 'X', 5: 'Z', 6: 'X', 7: 'Z', 8: 'Z', 9: 'Z', 10: 'X', 11: 'X', 12: 'Z', 13: 'Z', 14: 'X', 15: 'X'}

Entonces, si la clave no es correcta, entonces es la contraria:

>>> basis = {used[0][0]: 'Z'}
>>>
>>> while len(basis) < len(used):
...     old_basis = basis.copy()
...     for u, m in old_basis.items():
...         for t, v in used_non_ambiguous.items():
...             if u == t[0] and v == '11,11' and t[1] not in basis:
...                 basis[t[1]] = 'Z' if m == 'X' else 'X'
...             elif u == t[1] and v == '11,11' and t[0] not in basis:
...                 basis[t[0]] = 'Z' if m == 'X' else 'X'
...             elif u == t[0] and v == '00,11' and t[1] not in basis:
...                 basis[t[1]] = m
...             elif u == t[1] and v == '00,11' and t[0] not in basis:
...                 basis[t[0]] = m
...     if len(old_basis) == len(basis):
...         break
...
>>> basis_z = basis
>>> basis_z
{2: 'Z', 15: 'X', 4: 'X', 9: 'Z', 6: 'X', 7: 'Z', 11: 'X', 3: 'Z'}
>>> _basis
{0: 'Z', 1: 'Z', 2: 'Z', 3: 'Z', 4: 'X', 5: 'Z', 6: 'X', 7: 'Z', 8: 'Z', 9: 'Z', 10: 'X', 11: 'X', 12: 'Z', 13: 'Z', 14: 'X', 15: 'X'}

Obsérvese que no necesitamos encontrar todas las bases de medición, solo los índices que realmente se usan para la generación del secreto. Ahora podemos usar el método generate_shared_key de Bob para encontrar la clave compartida:

>>> from helpers import BOB_MR_DERIVATION, KEY_DERIVATION
>>>
>>> def generate_shared_key(measurement_basis, frames, ambiguous_frames, sifting_strings):  
...     shared_secret = ''
...     for frame in frames:
...         if frame in ambiguous_frames:
...             continue
...         basis_orientation = (measurement_basis[frame[0]], measurement_basis[frame[1]])
...         measurement_result = BOB_MR_DERIVATION[basis_orientation]
...         shared_secret += KEY_DERIVATION[sifting_strings[frame]][measurement_result]
...     return shared_secret
...
>>> generate_shared_key(basis_x, frames, ambiguous_frames, bob_sifting_strings)
'101110111111'
>>> generate_shared_key(basis_z, frames, ambiguous_frames, bob_sifting_strings)
'010001000000'
>>> _shared_key.decode()
'010001000000'

En este punto, hemos encontrado una manera de encontrar la clave compartida con una probabilidad del 50%.

Consiguiendo la flag

Ahora solo necesitamos usar la clave compartida para obtener una clave AES y cifrar el comando solicitado ("OPEN THE GATE"):

    while True:
        try:
            data = json.loads(input("> "))
            encrypted_command = bytes.fromhex(data["command"])
            assert len(encrypted_command) % 16 == 0
        except:
            json_print({"error": "Invalid input. Please, try again"})
            continue

        command = qkd.decrypt_command(encrypted_command)
        
        if command == "OPEN THE GATE":
            FLAG = open('flag.txt').read()
            json_print({"info": f" Welcome to The Frontier Board, the coordinates of The Starry Spurr are {SECRET_MESSAGE}{FLAG}"})  
            exit()

        else:
            json_print({"error": "Unknown command. Please, try again"})

La función decrypt_command utiliza la clave compartida para derivar una clave AES. Luego, quita el relleno PKCS7, pero no hay un manejador de excepción:

    def decrypt_command(self, encrypted_command):
        key = sha256(self.shared_key).digest()

        cipher = AES.new(key, AES.MODE_ECB)
        command = unpad(cipher.decrypt(encrypted_command), 16)  
    
        return command.decode()

Por lo tanto, no podremos probar las dos posibles claves compartidas que obtuvimos antes, porque es muy probable que una clave AES incorrecta resulte en un relleno incorrecto y el servidor termine el programa. Pero esto no es un problema, porque obtendremos la clave compartida correcta una de cada dos veces.

Flag

Podemos juntar todos los fragmentos de código anteriores en un script de Python que se conecta a la instancia del reto, toma la información necesaria, extrae la clave compartida y la usa para cifrar el comando requerido. Con esto, podemos obtener la flag:

$ python3 solve.py 94.237.54.253:46816
[+] Opening connection to 94.237.54.253 on port 46816: Done
[+] Shared key: 0101010011011010111110011110011111111101011111101000010100101111110110001011100011011111010010011100010010101111010110110011010000101111001010001001101101011101101101111101001011101110110100101101011001000110010111100101110110010110010011101001111101100010101101111001100100110110011011100011000111100000011001000111110100100010100001011100011011110001110010100110101010101000111010001111111000000111000010101110110111101000010010101100001111010101001101010111011110100110111000010010100111101110111010110100100000000010011000001110001101111000000110001011100111001011101010110000010010110011110000101101000011011011110111101001101010011110100000111011010000110101100000010010001011100011101110101100111101111101111110101000100010100011101111110011010001001110  
[+] HTB{n0w_7h475_4_C1u7Ch!_d3f1n3731Y_Fr4m3_b453d_QKD_n33d5_70_M47ur3__C0ngr47u14710n5!_d546b1cc16212e806fac3136509fe5f8}
[*] Closed connection to 94.237.54.253 port 46816

El script completo se puede encontrar aquí: solve.py.

Conclusión

No todos los trabajos de investigación son perfectos. Este es un gran ejemplo de un algoritmo que se ve bastante complejo y difícil de romper, pero está completamente roto, a pesar de estar muy bien documentado. Quiero agradecer al autor, D-Cryp7, por este increíble reto, que me hizo profundizar en el protocolo de QKD intentando encontrar un fallo, aunque parecía ser bastante seguro a primera vista.