RSA Beginner

We are given these numbers:

e: 3
c: 174422460809195453539354885823735245900172562989776845322302
n: 245841236512478852752909734912575581815967630033049838269083

We have the exponent , the modulus and the ciphertext .

It is clear that we have an RSA cryptosystem. Let’s review how RSA works:

Two prime numbers and are chosen so that we have the modulus . Then an exponent is chosen (usually 3 or 65537) so that it is coprime with .

In order to encrypt a message (in numeric format), this operation must be performed:

So that is the ciphertext. And to decrypt the ciphertext, we must first calculate and then compute this:

At this point, the public key is the set , whereas the private key is formed by .

The RSA cryptosystem will be robust as far as the modulus is difficult to factorize. Otherwise, one could compute and from and therefore compute and .

This time, the modulus we have is relatively short, so we might be able to factorize it. For that purpose, we can go to factordb.com and introduce the modulus:

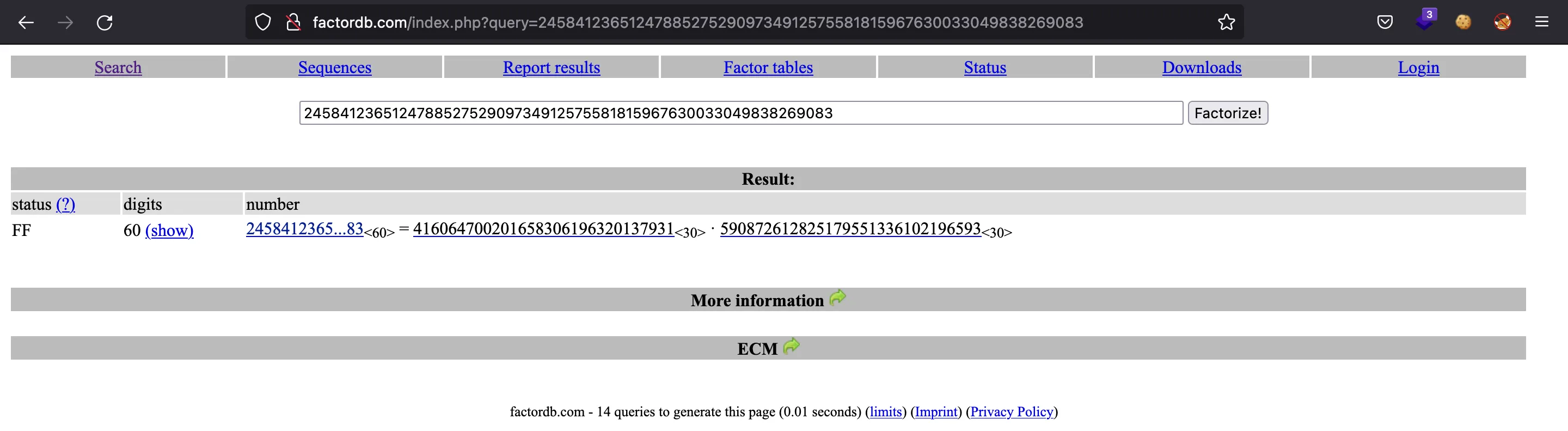
Now that we have and , we can use Python to compute and . And finally, compute the message :

$ python3 -q
>>> e = 3
>>> c = 174422460809195453539354885823735245900172562989776845322302
>>> n = 245841236512478852752909734912575581815967630033049838269083
>>> p = 416064700201658306196320137931
>>> q = 590872612825179551336102196593
>>> phi_n = (p - 1) * (q - 1)
>>> d = pow(e, -1, phi_n)
>>> m = pow(c, d, n)
>>> hex(m)
'0x4354466c6561726e7b7273345f69735f61773373306d337d'

Remember that the message is in numeric format, so we must decode it as ASCII bytes:

>>> bytes.fromhex('4354466c6561726e7b7273345f69735f61773373306d337d')
b'CTFlearn{rs4_is_aw3s0m3}'