AESWCM

5 minutes to read

We got the Python source code of the server:

from Crypto.Util.Padding import pad
from Crypto.Cipher import AES
import os
import random
from secret import FLAG

KEY = os.urandom(16)
IV = os.urandom(16)


class AESWCM:

    def __init__(self, key):
        self.key = key
        self.cipher = AES.new(self.key, AES.MODE_ECB)
        self.BLOCK_SIZE = 16

    def pad(self, pt):
        if len(pt) % self.BLOCK_SIZE != 0:
            pt = pad(pt, self.BLOCK_SIZE)
        return pt

    def blockify(self, message):
        return [
            message[i:i + self.BLOCK_SIZE]
            for i in range(0, len(message), self.BLOCK_SIZE)
        ]

    def xor(self, a, b):
        return bytes([aa ^ bb for aa, bb in zip(a, b)])

    def encrypt(self, pt, iv):
        blocks = self.blockify(pt)
        xor_block = iv

        ct = []
        for block in blocks:
            ct_block = self.cipher.encrypt(self.xor(block, xor_block))  
            xor_block = self.xor(block, ct_block)
            ct.append(ct_block)

        return b"".join(ct).hex()

    def decrypt(self, ct, iv):
        ct = bytes.fromhex(ct)
        blocks = self.blockify(ct)
        xor_block = iv

        pt = []
        for block in blocks:
            pt_block = self.xor(self.cipher.decrypt(block), xor_block)
            xor_block = self.xor(block, pt_block)
            pt.append(pt_block)

        return b"".join(pt)

    def tag(self, pt, iv=os.urandom(16)):
        blocks = self.blockify(bytes.fromhex(self.encrypt(pt, iv)))
        random.shuffle(blocks)

        ct = blocks[0]
        for i in range(1, len(blocks)):
            ct = self.xor(blocks[i], ct)

        return ct.hex()


def main():
    aes = AESWCM(KEY)
    tags = []
    properties = []
    print("What properties should your magic wand have?")
    message = "Property: "

    counter = 0
    while counter < 3:
        property = bytes.fromhex(input(message))
        property = aes.pad(message.encode() + property)

        if property not in properties:
            properties.append(property)

            property_tag = aes.tag(property, IV)
            tags.append(property_tag)
            print(property_tag)

            if len(tags) > len(set(tags)):
                print(FLAG)

            counter += 1
        else:
            print("Only different properties are allowed!")
            exit(1)


if __name__ == "__main__":
    main()

Source code analysis

First of all, the program initializes KEY and IV variables to 16 random bytes. After that, an instance of AESWCM class is created.

Then, we are asked to enter a message that will be tagged. Our message (property) will be appended to the messages list (properties). And the tag (property_tag) will be appended to the tags list (tags).

We will see the flag when len(tags) > len(set(tags)); that is, when there is a repeated element in tags (because there are no duplicated elements in a set).

The code below reflects the above explanation:

    message = "Property: "

    counter = 0
    while counter < 3:
        property = bytes.fromhex(input(message))
        property = aes.pad(message.encode() + property)

        if property not in properties:
            properties.append(property)

            property_tag = aes.tag(property, IV)
            tags.append(property_tag)
            print(property_tag)

            if len(tags) > len(set(tags)):
                print(FLAG)

            counter += 1
        else:
            print("Only different properties are allowed!")  
            exit(1)

Analyzing the encryption algorithm

The way of tagging a message (property) is by calling the tag method (that is "Property: " plus our input data).

This is the tag method:

    def tag(self, pt, iv=os.urandom(16)):
        blocks = self.blockify(bytes.fromhex(self.encrypt(pt, iv)))  
        random.shuffle(blocks)

        ct = blocks[0]
        for i in range(1, len(blocks)):
            ct = self.xor(blocks[i], ct)

        return ct.hex()

What it does is: it encrypts the plaintext using method encrypt, splits the result in blocks of 16 bytes using blockify and finally, it shuffles the blocks and applies XOR to all of them.

Here we can see that the shuffle is useless, because XOR is commutative, the order does not matter.

Use of AES and XOR

The method encrypt is this one:

    def encrypt(self, pt, iv):
        blocks = self.blockify(pt)
        xor_block = iv

        ct = []
        for block in blocks:
            ct_block = self.cipher.encrypt(self.xor(block, xor_block))  
            xor_block = self.xor(block, ct_block)
            ct.append(ct_block)

        return b"".join(ct).hex()

Basically, the plaintext is divided into 16-byte blocks and does the encryption. Let’s recall that the cipher is AES ECB:

class AESWCM:

    def __init__(self, key):
        self.key = key
        self.cipher = AES.new(self.key, AES.MODE_ECB)  
        self.BLOCK_SIZE = 16

However, the encrypt function is rather similar to AES CBC mode, but not exactly the same. Below, you can see how is AES CBC encryption:

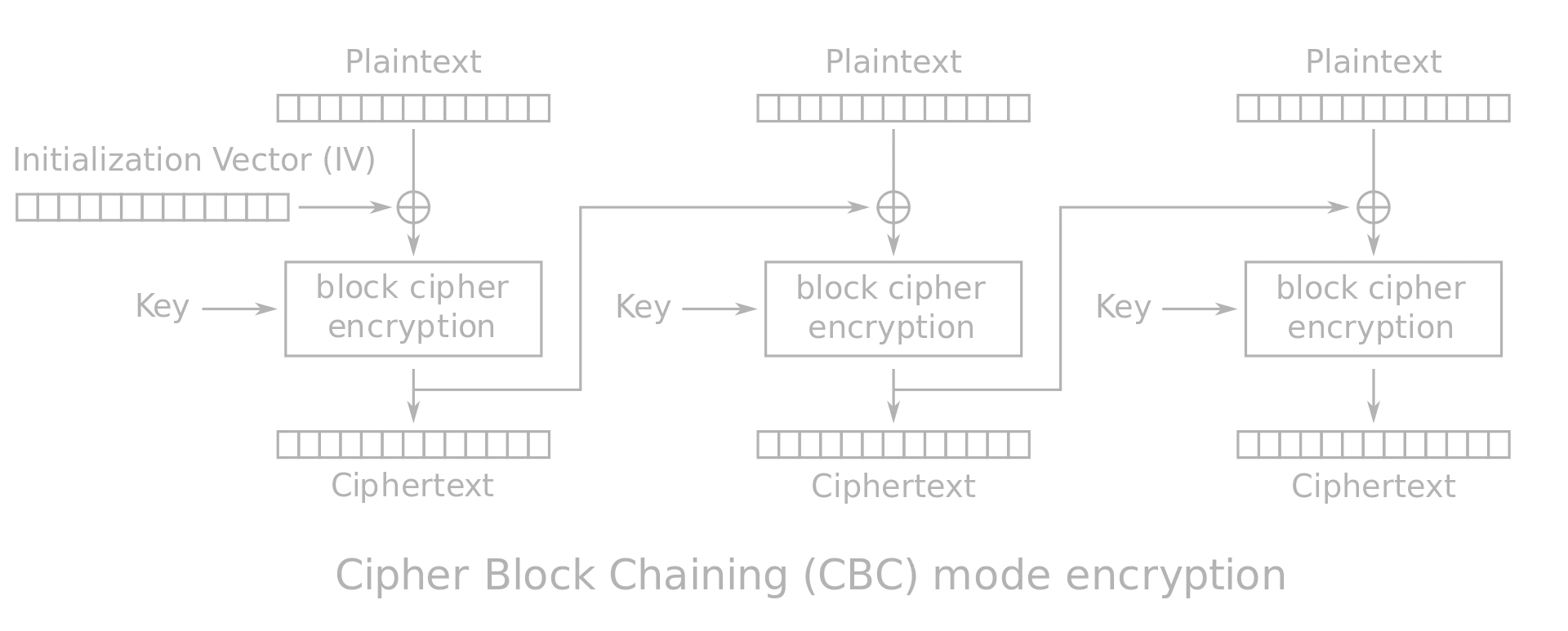
AESWCM 1

This time, the feedbacks from each block to the next are not the ciphertext blocks, but a XOR between the ciphertext blocks with the plaintext blocks. Say we have 3 plaintext blocks ($p_1$, $p_2$, $p_3$):

$$ c_1 = \mathrm{AES}\big(p_1 \oplus \mathrm{IV}\big) $$ $$ c_2 = \mathrm{AES}\big(p_2 \oplus (p_1 \oplus c_1)\big) $$ $$ c_3 = \mathrm{AES}\big(p_3 \oplus (p_2 \oplus c_2)\big) $$

Solution

For the solution we are going to avoid padding entering messages sized a multiple of 16 bytes. Let $p_{i,j}$ be the plaintext message we send to the server, $c_{i,j}$ the output of the AES encryption and $e_i$ the result of the XOR operation between the blocks, where $i$ represents the round number and $j$ is the index of the block.

For the first round we will enter a single block, and we will have $e_1 = c_{1,1}$, where

$c_{1,1} = \mathrm{AES}(p_{1,1} \oplus \mathrm{IV})$.

Then we will set:

$p_{2,1} = p_{1,1}$
$p_{2,2} = e_1 \oplus p_{1,1}$

So $e_2 = c_{2,1} \oplus c_{2,2}$, where

$c_{2,1} = \mathrm{AES}(p_{2,1} \oplus \mathrm{IV})$
$c_{2,2} = \mathrm{AES}\big(p_{2,2} \oplus (p_{2,1} \oplus c_{2,1})\big)$.

Notice that $c_{2,1} = c_{1,1} = e_1$ and

$$ c_{2,2} = \mathrm{AES}\big((e_1 \oplus p_{1,1}) \oplus (p_{1,1} \oplus e_1)\big) = \mathrm{AES}(0) $$

Then we can simplify $e_2 = e_1 \oplus \mathrm{AES}(0)$.

Finally, we will set

$p_{3,1} = p_{2,1}$
$p_{3,2} = p_{2,2}$
$p_{3,3} = p_{2,2} \oplus c_{2,2}$

Then we have $e_3 = c_{3,1} \oplus c_{3,2} \oplus c_{3,3}$, where

$c_{3,1} = \mathrm{AES}(p_{3,1} \oplus \mathrm{IV})$
$c_{3,2} = \mathrm{AES}\big(p_{3,2} \oplus (p_{3,1} \oplus c_{3,1})\big)$
$c_{3,3} = \mathrm{AES}\big(p_{3,3} \oplus (p_{3,2} \oplus c_{3,2})\big)$

Notice that

$c_{3,1} = c_{2,1} = c_{1,1} = e_1$
$c_{3,2} = c_{2,2} = \mathrm{AES}(0)$

On the other hand,

$$ c_{3,3} = \mathrm{AES}\big((p_{2,2} \oplus c_{2,2}) \oplus (p_{3,2} \oplus c_{3,2})\big) = \mathrm{AES}(0) $$

Then we will have $e_3 = c_{3,1} \oplus c_{3,2} \oplus c_{3,3} = e_1 \oplus \mathrm{AES}(0) \oplus \mathrm{AES}(0) = e_1$.

Since $e_3 = e_1$, then the list of tags will have a duplicated element and we will get the flag.

Implementation in Python

def main():
    io = get_process()

    p_1_1 = b'Property: ' + bytes.fromhex('00' * 6)

    io.sendlineafter(b'Property: ', p_1_1[10:].hex().encode())
    e_1 = c_1_1 = bytes.fromhex(io.recvline().decode())

    p_2_1 = p_1_1
    p_2_2 = xor(e_1, p_1_1)

    io.sendlineafter(b'Property: ', (p_2_1 + p_2_2)[10:].hex().encode())
    e_2 = bytes.fromhex(io.recvline().decode())

    c_2_1 = c_1_1
    c_2_2 = xor(e_2, c_2_1)

    p_3_1 = p_2_1
    p_3_2 = p_2_2
    p_3_3 = xor(p_2_2, c_2_2)

    io.sendlineafter(b'Property: ', (p_3_1 + p_3_2 + p_3_3)[10:].hex().encode())  
    io.recvline()
    log.success(f'Flag: {io.recvline()}')
    io.close()

$ python3 solve.py 178.62.21.211:32535
[+] Opening connection to 178.62.21.211 on port 32535: Done  
[+] Flag: b'HTB{435_cu570m_m0d35_4nd_hm4c_423_fun}'
[*] Closed connection to 178.62.21.211 port 32535

The full script can be found in here: solve.py.