Find Marher's Secret
5 minutes to read
We are given a some Python source code and a server to connect to:
$ nc 161.35.172.25 32275
Connected to the cyborg's debugging interface
Options:
1. Encrypt your text.
2. Claim the key.
>
Static code analysis
This is the relevant part of the code:
def challenge(req):
key = bytes.fromhex(KEY)
assert(len(key) == 27)
req.sendall(b'Connected to the cyborg\'s debugging interface\n')
while True:
req.sendall(
b'\nOptions:\n1. Encrypt your text.\n2. Claim the key.\n> ')
try:
response = json.loads(req.recv(4096).decode())
if response['option'] == 'encrypt':
iv = bytes.fromhex(response['iv'])
pt = bytes.fromhex(response['pt'])
ct = encrypt(key, iv, pt)
payload = {'response': 'success',
'pt': response['pt'], 'ct': ct}
payload = json.dumps(payload)
req.sendall(payload.encode())
elif response['option'] == 'claim':
answer = bytes.fromhex(response['key'])
if hashlib.sha256(answer).hexdigest() == hashlib.sha256(key).hexdigest():
payload = {'response': 'success', 'flag': FLAG}
payload = json.dumps(payload)
req.sendall(payload.encode())
else:
payload = {'response': 'fail',
'message': 'Better luck next time.'}
payload = json.dumps(payload)
req.sendall(payload.encode())
else:
payload = {'response': 'error', 'message': 'Invalid option!'}
payload = json.dumps(payload)
req.sendall(payload.encode())
except Exception as e:
payload = json.dumps(
{'response': 'error', 'message': 'An error occured!'})
req.sendall(payload.encode())
return
First of all, we see that we need to interact with the server using JSON-formatted messages.
Moreover, we can send arbitrary text messages to the server and they will be encrypted using RC4 as follows:
def encrypt(key, iv, pt):
return ARC4.new(iv + key).encrypt(pt).hex()
Notice that we also need to provide the IV, because the RC4 cipher is created from iv + key.
In order to get the flag, we must extract the secret key, which we know is 27 bytes long.
FMS attack
There is a well-known attack on cryptosystems that use RC4, such as WEP protocol for Wi-Fi (which is fully broken). This attack is the Fluhrer, Mantin and Shamir attack (FMS attack in short). Notice that the accronym of the challenge name is a hint that points to this attack.
RC4 is a stream cipher that works as follows:
Basically, a stream cipher has an input key and outputs a random bit stream, so that the encryption is the XOR between the bit stream and the plaintext bits. Using the same key will result in the same bit stream.
The following explanation is based mainly on these resources:
And for the solution script, I will adapt the source code of FMS-Attack.
Brief explanation
RC4 uses several S-Box to generate the bit stream. Following the above paper, on Section 7.1, we have the same situation on this challenge. That is, we control the IV and it is prepended to the secret key before creating the RC4 cipher.
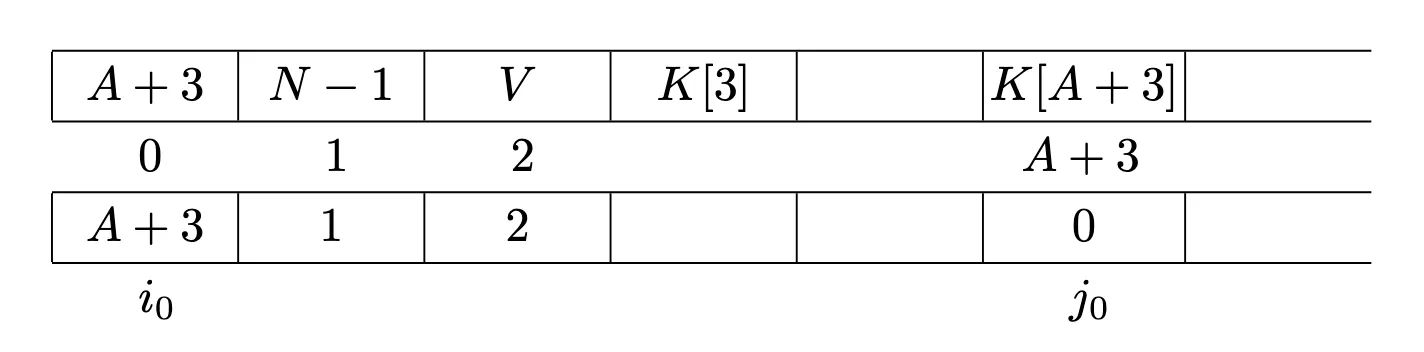
Let’s define $K$ as the input key for the RC4 cipher, and $\mathrm{SK}$ the actual secret key. Also. let $L$ be the length of the key. For convenience, the IV will only have 3 values. Therefore:
$$ K[0 .. L - 1] = [ \mathrm{IV}[0], \mathrm{IV}[1], \mathrm{IV}[2], \mathrm{SK}[0], \mathrm{SK}[1], \dots, \mathrm{SK}[L - 4]] $$
The issue is that using $\mathrm{IV} = [A + 3, N - 1, V]$ we will be able to recover the byte $K[A + 3]$ with high probability. This happens because on each iteration of the Key Schedule Algorithm (KSA) some bytes are swapped by index, and there is a resolved condition where $\mathrm{KSB}[0] = S[S[1] + S[j]]$, where $\mathrm{KSB}$ stands for the key stream bytes (the output of the RC4 cipher).
The first two elements of the IV are crafted so that the first round swaps indices $0$ and $A + 3$ (because index i starts at $0$ and j starts a $0$ as well, but it is updated to j = (j + s[i]) % 256, which is $A + 3$):
The second iteration swaps indices $1$ and $A + 3$, because i is increased by one and j is updated as j = (j + s[i]) % 256, which happens to be unchanged:
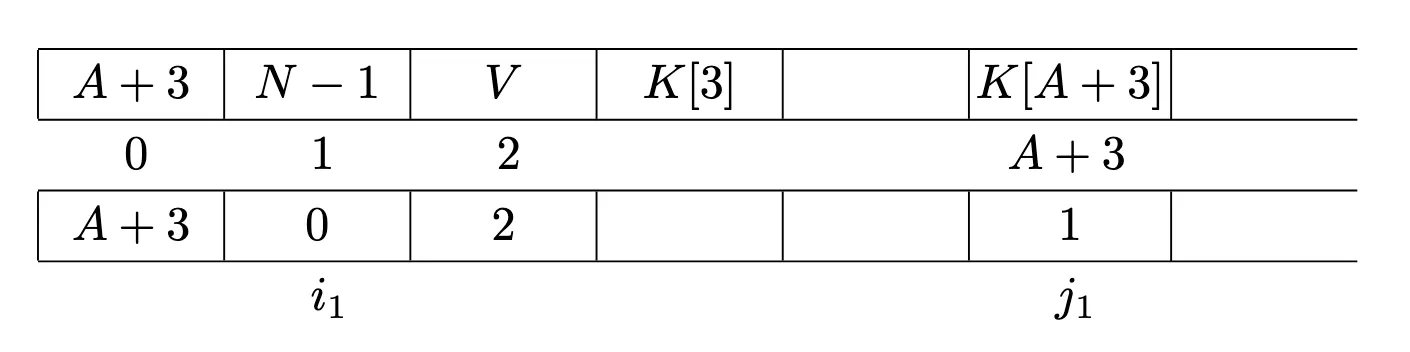
As the paper says: on the next round, j is advanced by $V + 2$, which implies that each distinct IV assigns a different value to j, and thus beyond this point, each IV acts differently. Since the attacker knows the value of $V$ and $K[3], \dots, K[A + 2]$, he can compute the exact behavior of the key setup until before round $A + 3$. At this point, he knows the value of j at iteration $A + 2$ and the exact values of the permutation. If the value at indices $0$ and $1$ have been disturbed, the attacker discards this IV. Otherwise, j is advanced by $S_{A + 2}[i_{A + 3}] + K[A + 3]$, and then the swap is done, resulting in the below structure:
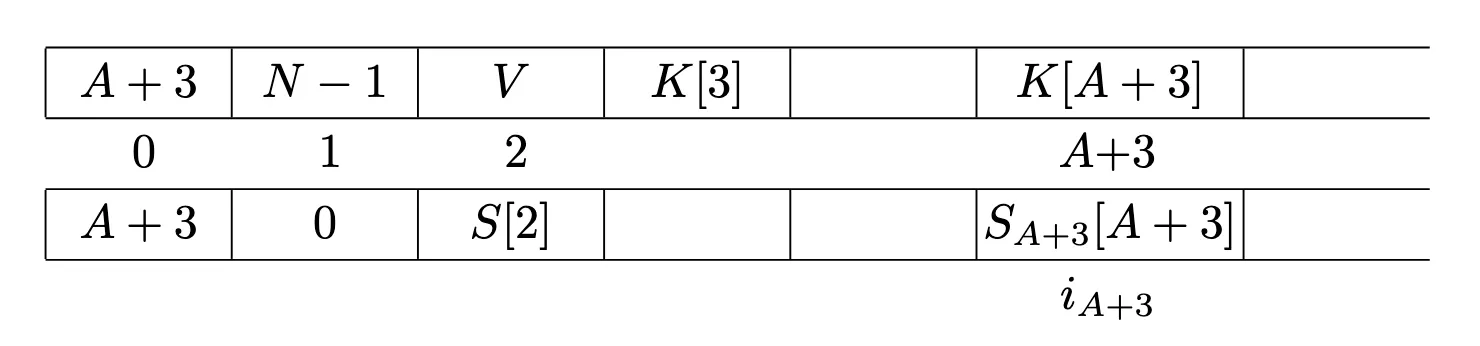
Solution script
There are two important scripts in FMS-Attack. One of them is WEPOutput.py, which generates the cipher and stores the output values in a CSV file; and keyRecover.py, which takes the CSV file and extracts the key with the FMS attack.
To solve the challenge, I combined the two scripts and removed the CSV file for storing intermediate values. Instead, we need to use the server to generate the necessary values to perform the FMS attack.
This attack works in WEP because the plaintext always starts with aa (in hexadecimal), which is part of the SNAP header. We can use any other byte, but I kept it as is.
Flag
If we run the solution script, we will find the flag (it can take quite a few minutes):
$ python3 solve.py 161.35.172.25:32275
[+] Opening connection to 161.35.172.25 on port 32275: Done
[+] A: 27
[+] Key: A1DD163ADAC252ADE631A89A203C2BE92B981EAAE6DAC3044EACE1
[+] Flag: HTB{7h3_FMS_@tt3ck_br0k3_@_l0t_0f_th17gs_i7_w1f1!!}
[*] Closed connection to 161.35.172.25 port 32275
The full script can be found in here: solve.py.