Nuclear Sale
2 minutes to read
We are given a PCAP file (challenge.pcap). If we analyze it using Wireshark, we will see some SMTP emails:
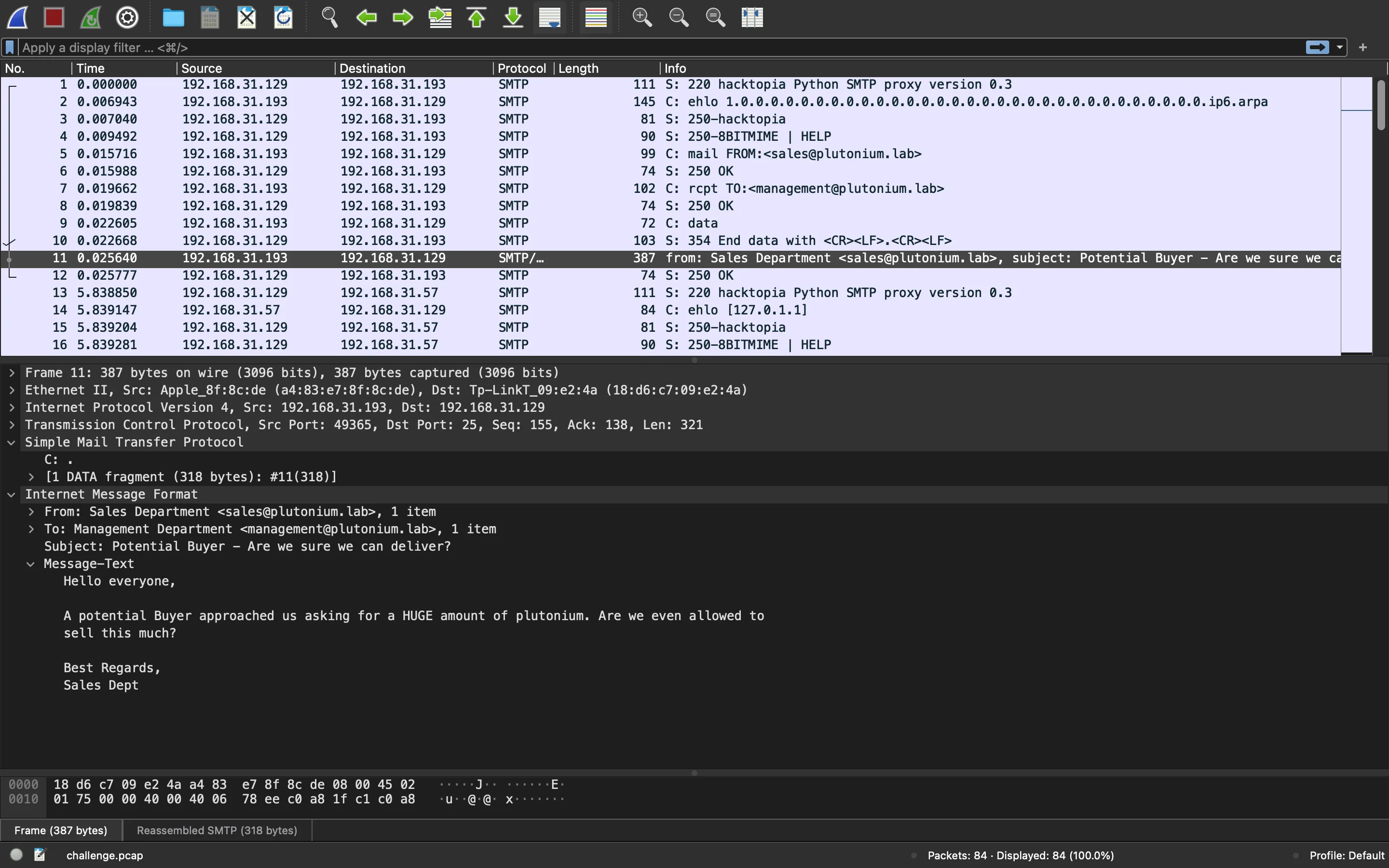
The challenge is based on a series of emails sent within a company. There is some information encrypted there. These are the emails:
Hello everyone,
A potential Buyer approached us asking for a HUGE amount of plutonium. Are we even allowed to
sell this much?
Best Regards,
Sales Dept
We are very XORry but the management does not approve such a sale. It may damage our business.
Who is the buyer?
Best Regards,
Management
He is a high profile individual. His information is encrypted below:
6b65813f4fe991efe2042f79988a3b2f2559d358e55f2fa373e53b1965b5bb2b175cf039
You know what you have to do.
Best Regards,
Sales Dept
Here is the ciphertext encrypted with our key.
fd034c32294bfa6ab44a28892e75c4f24d8e71b41cfb9a81a634b90e6238443a813a3d34
Best Regards,
Management
Encrypting again with our key...
de328f76159108f7653a5883decb8dec06b0fd9bc8d0dd7dade1f04836b8a07da20bfe70
Best Regards,
Sales Dept
Oh my... This changes everything. We cannot refuse selling to this guy. He can literally destroy us.
Move the process.
Best Regards,
Management
Alright, we will process the order. Thanks!
Best Regards,
Sales Dept
There is a hint in the second email telling that XOR cipher will be used (“We are very XORry”). Then, we have three hexadecimal strings that might be the result of XOR ciphers.
The above ciphertexts (in order,
Because of XOR properties:
And then
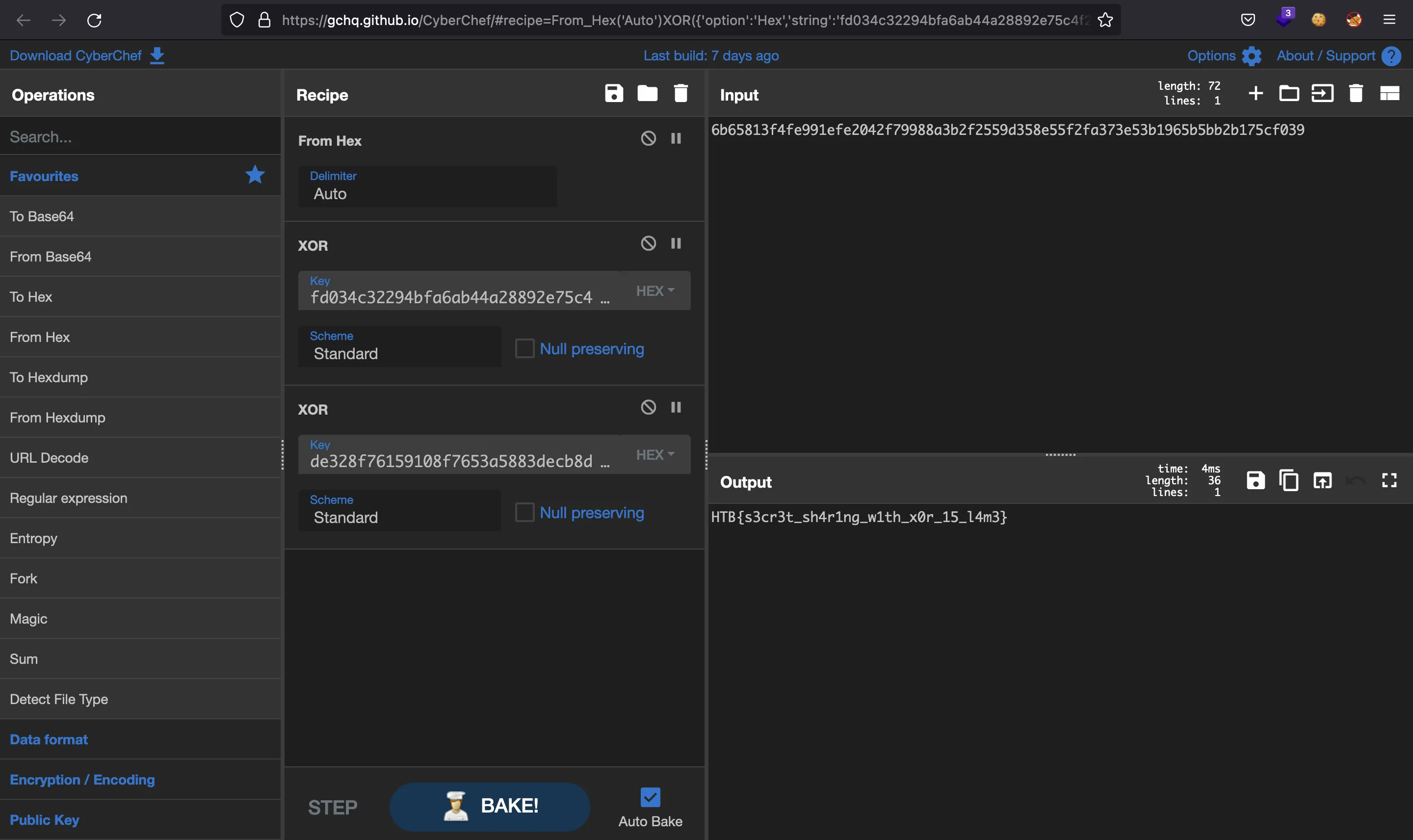
This can be easily done with CyberChef:
And also in Python:
$ python3 -q
>>> from pwn import unhex, xor
>>> c0 = unhex('6b65813f4fe991efe2042f79988a3b2f2559d358e55f2fa373e53b1965b5bb2b175cf039')
>>> c1 = unhex('fd034c32294bfa6ab44a28892e75c4f24d8e71b41cfb9a81a634b90e6238443a813a3d34')
>>> c2 = unhex('de328f76159108f7653a5883decb8dec06b0fd9bc8d0dd7dade1f04836b8a07da20bfe70')
>>> xor(c0, c1, c2)
b'HTB{s3cr3t_sh4r1ng_w1th_x0r_15_l4m3}'