Branching Tactics
5 minutes to read
We are given a remote instance to connect to:
$ nc 94.237.49.212 45041
You have a set of troops tasked with placing tnt in the underground tunnel. For every scenario, you will have the below values:
1. The n number of nodes in the terrain, where 2 <= n <= 3 * 10 ** 5.
2. The following n-1 lines will have 2 numbers e1, e2. These will both be nodes of the tunnels, where 1 <= e1, e2 <= n. The pair of nodes e1, e2 are connected.
3. The next number is m, the number of troops carrying tnt, where 1 <= m <= n.
4. m lines will follow, each with 3 values: s (the starting node of the troop), d (the destination node of the troop), and e (the energy of the troop), where 1 <= s, d, e <= n.
Each troop does their best job to move from nodes s to d, but can only make a maximum of e movements between nodes. The troop tries to get as far as possible with what energy it has.
Each movement from one node to another costs 1 energy, decreasing e by 1 - once e is at 0, the troop can not make another move.
Find the node each troop ends up in and place the tnt. Send the node e, in the same order as you received the s-d-e triplets.
Example Scenario:
3
3 2
2 1
2
1 1 1
1 3 1
Example Response:
1
2
Test 1/100
2
1 2
1
1 2 2
Problem statement
In this challenge, we are required to program an algorithm to solve the above problem a total of 100 times. On each round, we are given a graph with $n$ nodes and $n - 1$ edges connecting nodes. Then, on this graph, we have a troop that starts at node $s$ and wants to deliver TNT to node $d$ in a maximum of $e$ steps (each edge costs $1$ step).
We need to tell on which node will the troop arrive when it runs out of $e$ steps, or the destination $d$ if it manages to get within the effort limit.
Breadth-first Search
One suitable algorithm to find the shortest path is Breadth-first Search (BFS). Basically, this algorithm starts from a root node of the graph, marks it as visited, takes the adjacent nodes and puts them in a queue. Then, iteratively, for each node in the queue, it marks it as visited and it finds the adjacent nodes and inserts them in the queue. This process continues until reaching the desired destination, which will be the shortest path:
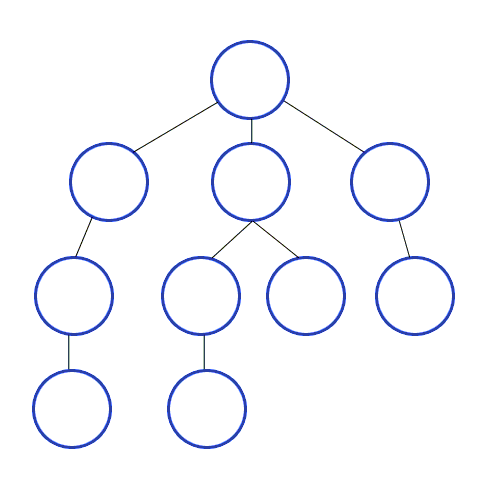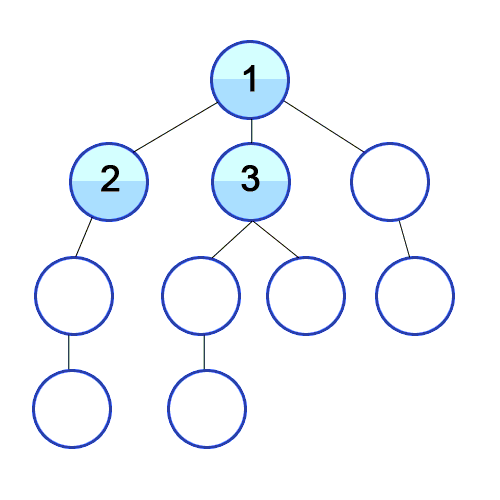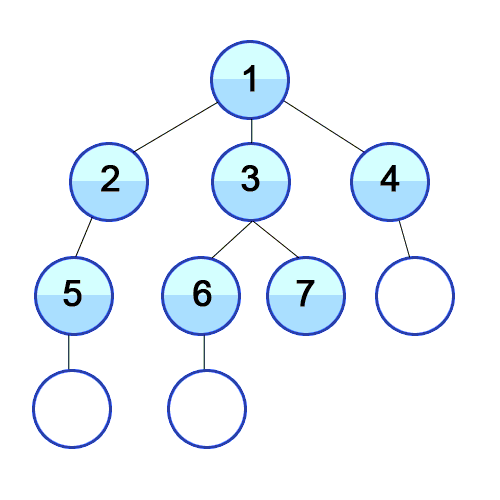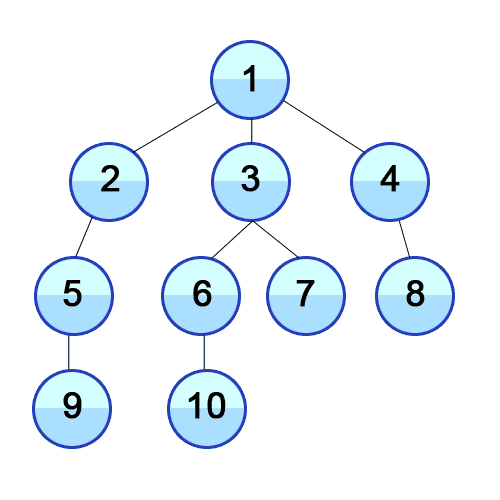
Source: https://commons.wikimedia.org/wiki/File:Breadth-First-Search-Algorithm.gif
Implementation
This algorithm can be implemented very easily in Go:
type path struct {
node int
path []int
}
func bfs(s, d int, edges map[int][]int) []int {
queue := []path{{node: s, path: []int{s}}}
visited := map[int]bool{}
for len(queue) > 0 {
n := queue[0]
queue = queue[1:]
visited[n.node] = true
if n.node == d {
return n.path
}
for _, v := range edges[n.node] {
if !visited[v] {
queue = append(queue, path{node: v, path: slices.Concat(n.path, []int{v})})
}
}
}
return []int{}
}
Notice that I used a path structure to store the current node and the current path up to that node. Hence, when we reach the destination, we will return the path, which will be the shortest.
To solve the challenge, we only need to see if the troop can make it to the destination in $e$ steps. If not, we take the node in the path at that position:
func solve(s, d, e int, edges map[int][]int) int {
path := bfs(s, d, edges)
if e >= len(path) {
return d
} else {
return path[e]
}
}
Last but not least, this is main, which uses my gopwntools module to parse the information send by the remote instance on each round and calls solve to return the solutions:
func main() {
hostPort := strings.Split(os.Args[1], ":")
io := pwn.Remote(hostPort[0], hostPort[1])
defer io.Close()
prog := pwn.Progress("Round")
for range 100 {
io.RecvUntil([]byte("Test"))
prog.Status(strings.TrimSpace(io.RecvLineS()))
n, _ := strconv.Atoi(strings.TrimSpace(io.RecvLineS()))
edges := map[int][]int{}
for i := 0; i < n-1; i++ {
e1, _ := strconv.Atoi(strings.TrimSpace(io.RecvUntilS([]byte{' '})))
e2, _ := strconv.Atoi(strings.TrimSpace(io.RecvLineS()))
edges[e1] = append(edges[e1], e2)
edges[e2] = append(edges[e2], e1)
}
m, _ := strconv.Atoi(strings.TrimSpace(io.RecvLineS()))
for i := 0; i < m; i++ {
s, _ := strconv.Atoi(strings.TrimSpace(io.RecvUntilS([]byte{' '})))
d, _ := strconv.Atoi(strings.TrimSpace(io.RecvUntilS([]byte{' '})))
e, _ := strconv.Atoi(strings.TrimSpace(io.RecvLineS()))
res := solve(s, d, e, edges)
io.SendLine([]byte(strconv.Itoa(res)))
}
}
prog.Success("100/100")
io.RecvUntil([]byte("HTB{"))
pwn.Success("HTB{" + io.RecvLineS())
}
Flag
If we execute the above script, we will get the flag:
$ go run solve.go 94.237.49.212:45041
[+] Opening connection to 94.237.49.212 on port 45041: Done
[+] Round: 100/100
[+] HTB{tReE_tR3e_4nD_Tr33_aG4iN!}
[*] Closed connection to 94.237.49.212 port 45041
As you can see, the flag talks about trees, which is a very common data structure in coding challenges. There are better algorithms to solve this challenge, such as Least Common Ancestor (LCA). However, the problem statement was not clear enough to me to ensure that all the graphs were going to be trees. For instance, although the graph has $n$ nodes and $n - 1$ edges, it is never said that there are no loops, or isolated nodes on the graph. That’s why I used BFS in this case, which is a more general algorithm. It worked, although not been the most efficient algorithm for this problem.
The full script can be found in here: solve.go.