Path of Survival
4 minutes to read
We are given the following website:
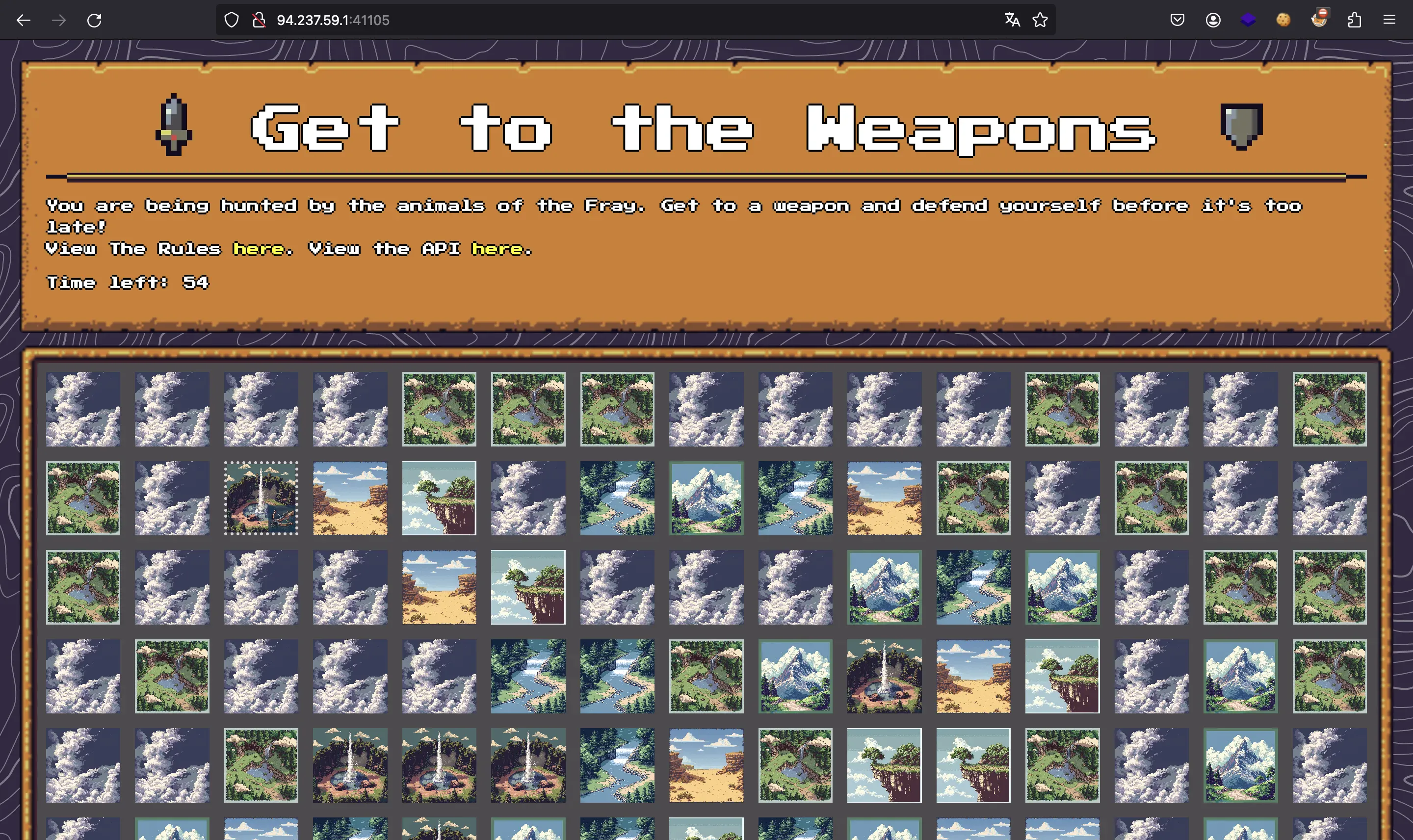
It shows a kind of labyrinth where we are an astronaut and we need to find a weapon in the shortest time possible.
The website shows how to interact with our astronaut player, and shows some rules regarding labyrinth tiles (Cliff, Geyser, Mountain…):
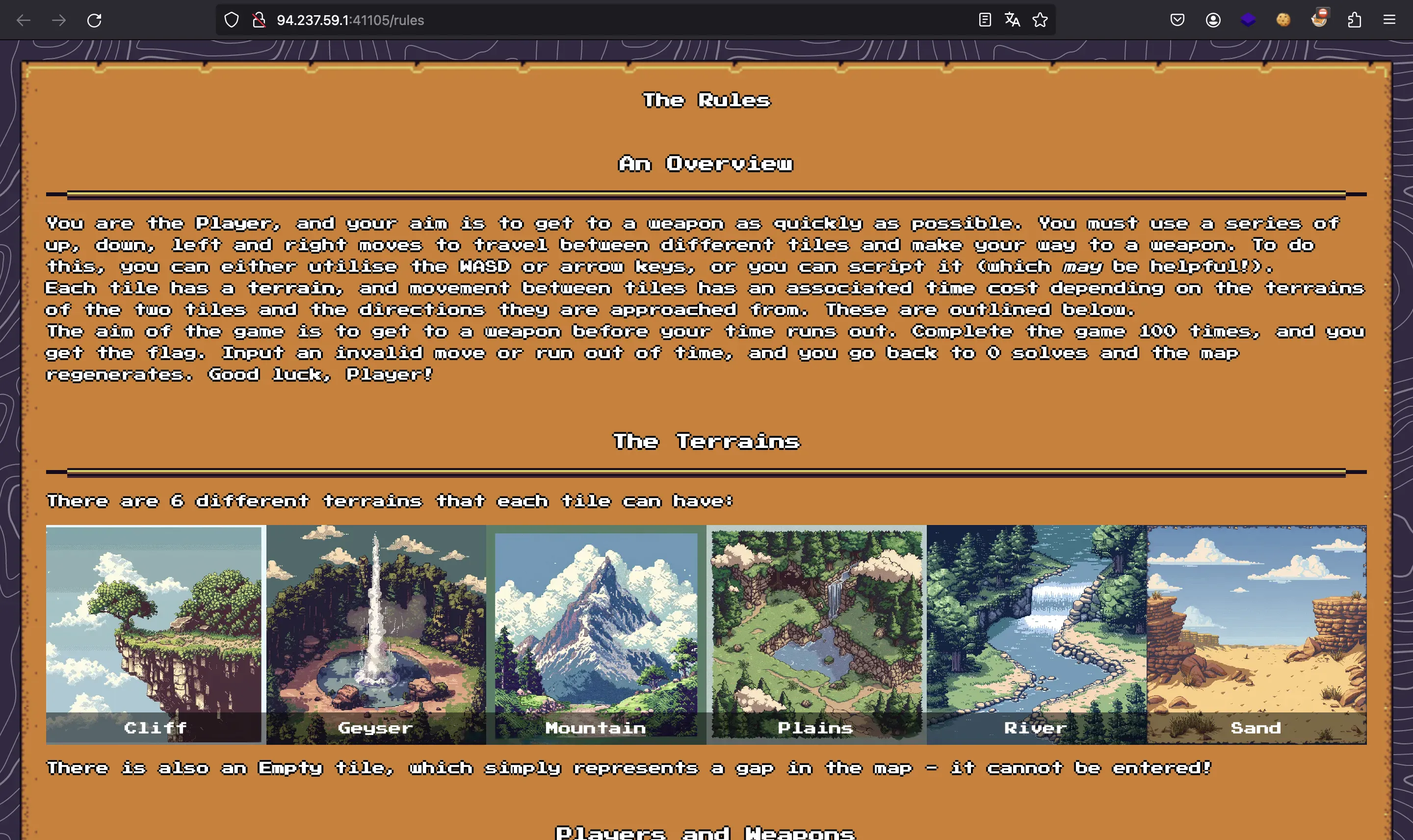
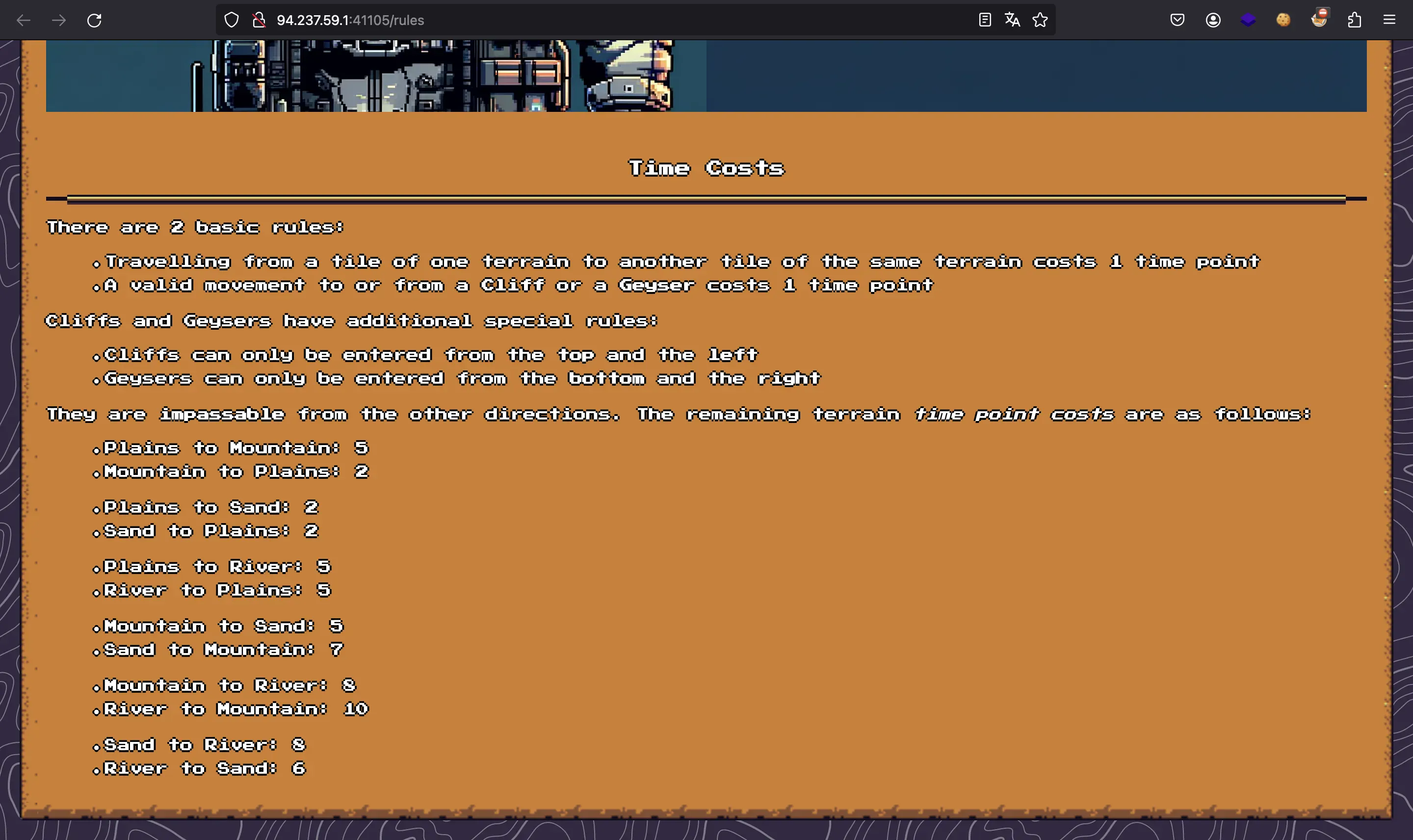
Moreover, we have an HTTP API to get the map as a JSON document and to run commands to move the astronaut:
Path-finding
The most suitable algorithm to find a weapon on the map in the shortest time possible is Dijkstra’s algorithm. This algorithm consists of building a weighted graph where the nodes are the map tiles and the edges are the direct connections between tiles, with their corresponding time cost.
Once the graph is completed, the algorithm takes the origin and updates all the costs to all the different positions of the graph, so that we have the time needed to reach any tile on the map. Finally, we can look for a weapon on the map that we can reach within the time limit set by the challenge.
Breadth-first Search
However, I used another path-finding algorithm which is Breadth-first Search (BFS), because I am more used to it.
Basically, this algorithm starts from a root node of the graph, marks it as visited, takes the adjacent nodes and puts them in a queue. Then, iteratively, for each node in the queue, it marks it as visited and it finds the adjacent nodes and inserts them in the queue. This process continues until reaching the desired destination, which will be the shortest path:
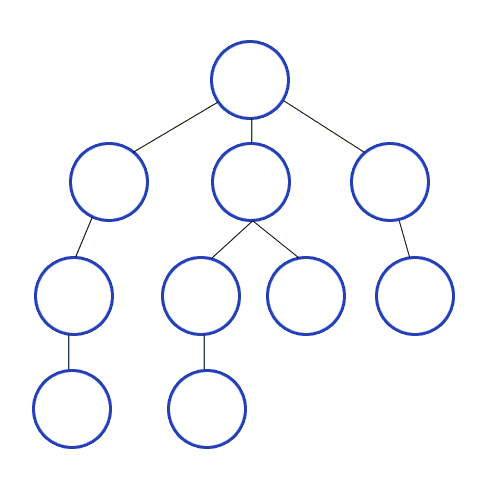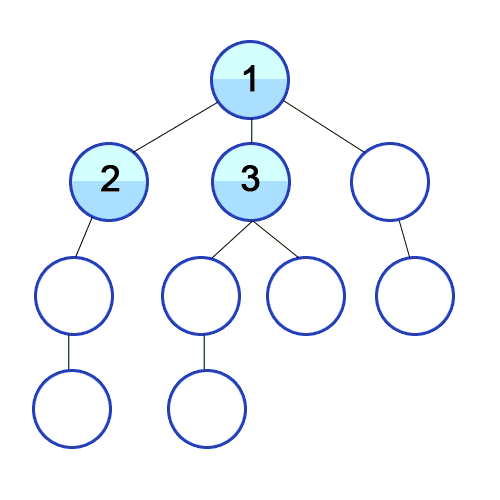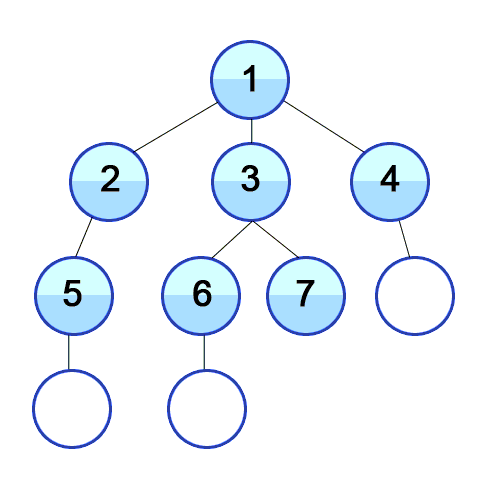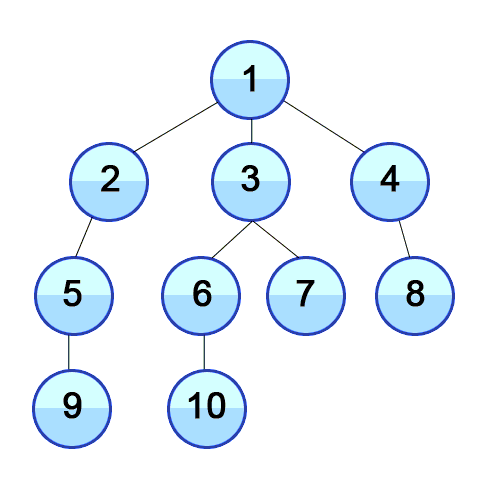
Source: https://commons.wikimedia.org/wiki/File:Breadth-First-Search-Algorithm.gif
Implementation
First of all, we need to download the map and parse it. For this, we will define three helper function to interact with the API:
def get_map():
map_data = requests.post(f'{URL}/map').json()
time = map_data.get('player').get('time')
orig_coords = tuple(map_data.get('player').get('position'))
orig = orig_coords[0] + 1j * orig_coords[1]
weapons = set()
map_tiles = {}
for coord, tile_data in map_data.get('tiles').items():
if tile_data.get('has_weapon'):
dest_coords = ast.literal_eval(coord)
weapons.add(dest_coords[0] + 1j * dest_coords[1])
x, y = ast.literal_eval(coord)
map_tiles[x + 1j * y] = tile_data.get('terrain')
return map_tiles, orig, weapons, time
def update(direction):
return requests.post(f'{URL}/update', json={'direction': direction}).json()
def regenerate():
requests.get(f'{URL}/regenerate')
The core part of the solution script is the BFS algorithm:
def bfs(root, map_tiles):
queue = deque([root])
visited_states = {(root, time)}
while len(queue):
pos, time_left, path = queue.popleft()
if time_left < 0:
continue
if (current_tile := map_tiles.get(pos)) is None:
continue
next_pos = [pos - 1, pos + 1, pos - 1j, pos + 1j]
for n in next_pos:
tile = map_tiles.get(n, 'E')
if tile == 'E':
continue
if tile == 'G' and n - pos in {1, 1j}:
continue
if tile == 'C' and n - pos in {-1, -1j}:
continue
new_time = time_left - terrain_costs.get(current_tile + tile, math.inf)
if new_time >= 0:
if n in weapons:
return path + (n, ), time_left
if (n, new_time) not in visited_states:
queue.append((n, new_time, path + (n, )))
visited_states.add((n, new_time))
return (), 0
The above code is quite standard, using collections.deque for performance, although we need to add the time left to the visited nodes in case we can reach a node in less time. Also, notice how I considered empty tiles, Geyser and Cliff.
Since we are using Python, coordinates
In order to know the costs between tiles, I used a dictionary where the first letter represents the origin and the second letter represents the destination:
terrain_costs = {
'PM': 5, 'MP': 2,
'PS': 2, 'SP': 2,
'PR': 5, 'RP': 5,
'MS': 5, 'SM': 7,
'MR': 8, 'RM': 10,
'SR': 8, 'RS': 6,
'PP': 1, 'MM': 1,
'SS': 1, 'RR': 1,
'CC': 1, 'GG': 1,
'PC': 1, 'CP': 1,
'MC': 1, 'CM': 1,
'SC': 1, 'CS': 1,
'RC': 1, 'CR': 1,
'GC': 1, 'CG': 1,
'PG': 1, 'GP': 1,
'MG': 1, 'GM': 1,
'SG': 1, 'GS': 1,
'RG': 1, 'GR': 1,
}
DIRECTIONS = {-1: 'L', 1: 'R', -1j: 'U', 1j: 'D'}
Finally, we need to run the algorithm 100 times to get the flag:
regenerate()
rounds = 1
round_prog = log.progress('Round')
while rounds <= 100:
map_tiles, orig, weapons, time = get_map()
root = (orig, time, (orig, ))
path, time_left = bfs(root, map_tiles)
round_prog.status(f'{rounds} / 100')
if not path and not time_left:
regenerate()
round_prog.failure('No path found')
round_prog = log.progress('Round')
rounds = 1
continue
path_tiles = list(map(map_tiles.get, path))
prev = orig
for coord in path[1:]:
direction = DIRECTIONS.get(coord - prev, '?')
data = update(direction)
prev = coord
if data.get('error'):
round_prog.failure(data)
round_prog = log.progress('Round')
rounds = 1
break
if (flag := data.get('flag')):
log.success(f'Flag: {flag}')
round_prog.success('100 / 100')
else:
rounds += 1
Flag
If we execute the above script, we will eventually get the flag:
$ python3 solve.py 94.237.59.1:41105
[+] Round: 100 / 100
[+] Flag: HTB{dIjKStr4_m4estRa_y0U_c4n_f1nD_tH3_p4Th!!!}
The full script can be found in here: solve.py.