Triangles

6 minutes to read

We are given the following Python source files:

triangulate.py:

import csv
import math
import random
from secret import getFlagLocation

arr = []
with open('grid.csv') as grid:
    for x in csv.reader(grid):
        arr.append(x)
        pass

def getDistance(x,y,x2,y2):
    return math.sqrt(math.pow(x - x2,2) + math.pow(y - y2,2))

def cap(num):
    if num > 99:
        return 99
    if num < 0:
        return 0
    return num

def createCoords(x,y):
    x1 = random.randint(-7,7)
    y1 = random.randint(-7,7)
    x2 = random.randint(-7,7)
    y2 = random.randint(-7,7)
    x3 = random.randint(-7,7)
    y3 = random.randint(-7,7)

    p1 = [cap(x1 + x), cap(y1 + y)]
    p2 = [cap(x2 + x), cap(y2 + y)]
    p3 = [cap(x3 + x), cap(y3 + y)]

    val1 = arr[p1[0]][p1[1]]
    val2 = arr[p2[0]][p2[1]]
    val3 = arr[p3[0]][p3[1]]

    distances = [(val1,getDistance(x,y,p1[0], p1[1])),(val2,getDistance(x,y,p2[0], p2[1])),(val3,getDistance(x,y,p3[0], p3[1])),(f"{val1}{val2}",getDistance(p1[0], p1[1],p2[0], p2[1])),(f"{val2}{val3}",getDistance(p2[0], p2[1],p3[0], p3[1])),(f"{val1}{val3}",getDistance(p1[0], p1[1],p3[0], p3[1]))]
    return distances

def createTriangulation():
    with open("out1.csv",'w') as out:
        writer = csv.writer(out)
        for coord in getFlagLocation():
            for val, dist in createCoords(coord[0],coord[1]):
                writer.writerow([val,dist])

def main():
    createTriangulation()

if __name__ == "__main__":
    main()

secret.py:

import csv

f = "HTB{fake_flag_for_testing}"

arr = []
with open('grid.csv') as grid:
    for x in csv.reader(grid):
        arr.append(x)
        pass

flagLocation = list()
# Coordinates are all placeholder values
flagLocation.append([1,2]) # H
flagLocation.append([2,2]) # T
flagLocation.append([3,2]) # B
flagLocation.append([4,2]) # {
flagLocation.append([55,2]) # f
flagLocation.append([65,2]) # a
flagLocation.append([75,2]) # k
flagLocation.append([85,2]) # e
flagLocation.append([9,25]) # _
flagLocation.append([5,2]) # f
flagLocation.append([6,2]) # l
flagLocation.append([7,2]) # a
flagLocation.append([8,2]) # g
flagLocation.append([9,2]) # _
flagLocation.append([1,12]) # f
flagLocation.append([2,22]) # o
flagLocation.append([3,32]) # r
flagLocation.append([4,12]) # _
flagLocation.append([5,22]) # t
flagLocation.append([6,32]) # e
flagLocation.append([7,22]) # s
flagLocation.append([8,42]) # t
flagLocation.append([9,52]) # i
flagLocation.append([12,2]) # n
flagLocation.append([11,2]) # g
flagLocation.append([13,2]) # }

def getFlagLocation():
    return flagLocation

def checkFlag():
    for i in range(len(f)):
        if arr[flagLocation[i][0]][flagLocation[i][1]] != f[i]:
            print("error")
            pass

And we also have two CSV files:

grid.csv:

P,1,<,:,M,A,T,b,3,*,V,T,C,E,c,:,$,Y,&,#,P,Y,8,#,f,*,y,T,e,^,C,J,I,I,e,e,r,Y,X,o,z,W,v,1,L,v,",",E,Z,A,Q,9,q,D,I,K,g,.,o,R,V,%,%,2,8,G,w,",",C,l,",",o,:,9,Z,#,T,B,",",W,t,q,c,n,p,2,G,A,6,{,R,v,L,q,j,m,T,:,V,3
u,g,^,R,*,;,>,s,y,D,o,V,J,r,@,I,3,},J,m,2,I,n,C,1,X,?,(,3,Y,o,k,g,W,3,:,8,k,u,m,i,0,m,c,h,b,O,3,3,},Y,.,],X,y,a,{,T,.,",",e,O,<,r,X,V,6,X,P,B,$,v,6,;,V,B,],w,(,*,f,T,*,>,2,",",R,U,x,z,>,5,.,f,&,1,3,3,F,I

...

},k,D,!,",",c,v,%,q,u,k,s,k,0,>,e,3,m,n,E,V,;,9,(,3,3,H,>,t,Y,&,k,b,S,l,^,i,[,0,*,m,R,%,P,D,^,*,0,t,Y,$,D,8,h,D,n,L,4,h,E,X,7,7,[,!,j,N,!,y,&,n,Q,.,5,u,W,&,I,A,X,.,[,q,6,f,K,M,k,[,&,3,d,),],8,},E,8,x,a

out.csv:

[,6.4031242374328485
p,5.0
4,2.23606797749979
[p,8.0
p4,2.8284271247461903
[4,6.324555320336759
X,7.211102550927978
1,7.211102550927978
5,7.0710678118654755
X1,8.0
15,11.045361017187261
X5,14.212670403551895

...

>,5.0
x,3.605551275463989
;,7.810249675906654
>x,7.0710678118654755
x;,4.242640687119285
>;,10.198039027185569

Source code analysis

As can be seen, secret.py uses a initial 2D-grid (grid.csv) and associates flag characters to coordinates within the grid. The flag shown in the given secret.py is just a placeholder, to understand the purpose of the script.

The main function in triangulate.py calls createTriangulation:

def createTriangulation():
    with open("out1.csv",'w') as out:
        writer = csv.writer(out)
        for coord in getFlagLocation():
            for val, dist in createCoords(coord[0],coord[1]):
                writer.writerow([val,dist])

def main():
    createTriangulation()

As can be seen, for each coordinate that comes from getFlagLocation (from secret.py), some lines are written to out.csv. These lines come from createCoords:

def createCoords(x,y):
    x1 = random.randint(-7,7)
    y1 = random.randint(-7,7)
    x2 = random.randint(-7,7)
    y2 = random.randint(-7,7)
    x3 = random.randint(-7,7)
    y3 = random.randint(-7,7)

    p1 = [cap(x1 + x), cap(y1 + y)]
    p2 = [cap(x2 + x), cap(y2 + y)]
    p3 = [cap(x3 + x), cap(y3 + y)]

    val1 = arr[p1[0]][p1[1]]
    val2 = arr[p2[0]][p2[1]]
    val3 = arr[p3[0]][p3[1]]

    distances = [(val1,getDistance(x,y,p1[0], p1[1])),(val2,getDistance(x,y,p2[0], p2[1])),(val3,getDistance(x,y,p3[0], p3[1])),(f"{val1}{val2}",getDistance(p1[0], p1[1],p2[0], p2[1])),(f"{val2}{val3}",getDistance(p2[0], p2[1],p3[0], p3[1])),(f"{val1}{val3}",getDistance(p1[0], p1[1],p3[0], p3[1]))]
    return distances

In math terms, this function receives the coordinates of a flag character as . It starts by generating three random points: , , . Those points are added to the flag coordinates:

Note that cap only limits the upper and lower limit within the grid:

def cap(num):
    if num > 99:
        return 99
    if num < 0:
        return 0
    return num

Next, val1, val2 and val3 are the characters that appear at coordinates , and , respectively, in the grid.

The function returns 6 tuples:

val1 and
val2 and
val3 and
val1, val2 and
val2, val3 and
val1, val3 and

Where represents the euclidean distance:

def getDistance(x,y,x2,y2):
    return math.sqrt(math.pow(x - x2,2) + math.pow(y - y2,2))

To sum up, for each flag character, we are given 6 lines in output. For instance, for the first character, we have:

[,6.4031242374328485
p,5.0
4,2.23606797749979
[p,8.0
p4,2.8284271247461903
[4,6.324555320336759

Solution

Let’s name some results:

Now, let’s draw an example:

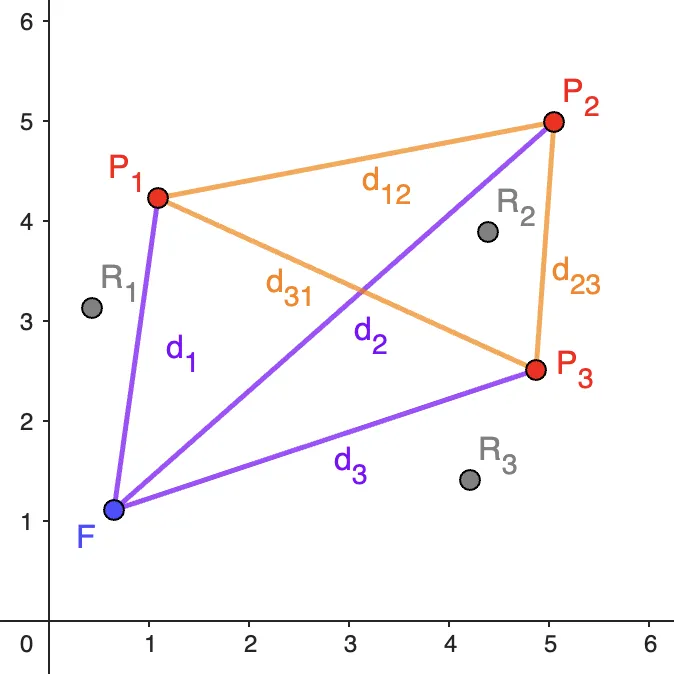
Triangles 1

Using only the distances, we are not able to locate the coordinates of the point , we will need the three points , or . If we had a single point , we can ensure that lies in a circumference of radious and center . If we have also , we know that lies in the intersection of circumferences of radious and and centers and , respectively. However, there are two intersections, so we need a third point to ensure a single point to locate .

In order to find suitable and and , we can try several points within the grid and test if they result in distances , and . Notice that we are given val1, val2 and val3, so we can take a few candidates for , and and test them.

Implementation

Let’s start wrinting the solution in a Python script. First of all, let’s read the CSV files and define the dictionary of values and coordinates that hold such values:

#!/usr/bin/env python3

import csv

from collections import defaultdict
from itertools import product


with open('grid.csv') as f_grid, open('out.csv') as f_out:
    grid = [row for row in csv.reader(f_grid)]
    results = f_out.read().splitlines()

values = defaultdict(list)

for x, row in enumerate(grid):
    for y, value in enumerate(row):
        values[value].append(x + 1j * y)

When dealing with 2D coordinates in Python (and Go), I like to use complex numbers, because it is easier to operate with them. For instance, the euclidean distance between two points is simply the absolute value of the difference of two complex numbers:

Now, for every sequence of 6 lines in out.csv (results), we will take val1, val2, val3 and the distances , , , , and :

for i in range(0, len(results), 6):
    val1, d1 = results[i + 0][:1], float(results[i + 0][2:])
    val2, d2 = results[i + 1][:1], float(results[i + 1][2:])
    val3, d3 = results[i + 2][:1], float(results[i + 2][2:])

    d12 = float(results[i + 3][3:])
    d23 = float(results[i + 4][3:])
    d31 = float(results[i + 5][3:])

First of all, we find points , , and by considering all combinations of points that hold val1, val2 and val3, and we find the one that has distances , and :

    for P1, P2, P3 in product(values[val1], values[val2], values[val3]):
        if abs(P1 - P2) == d12 and abs(P2 - P3) == d23 and abs(P3 - P1) == d31:
            break

Once those points are found, we iterate through all points in the grid (itererating the dictionary) and print the value of the point that has distances , and to points , and , respectively:

    for value, points in values.items():
        for F in points:
            if abs(F - P1) == d1 and abs(F - P2) == d2 and abs(F - P3) == d3:
                print(value, end='')
                break

Flag

If we run the script, we will get the flag:

$ python3 solve.py
HTB{sQU@r3s_R_4_N3rD$}

The full script can be found in here: solve.py.