<- CORCTF

two-wrongs

18 minutes to read

We are provided with the Python source code that encrypts the flag:

from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile
from qiskit_aer import AerSimulator
import numpy as np
import random, os, binascii, sys
from Crypto.Cipher import AES
from flag import flag

key = os.urandom(16)
cipher = AES.new(key, AES.MODE_ECB)

sv_sim = AerSimulator(method="statevector")
bit_idxs = list(map(int, input('Select a sensor index to remove from each bit: ').split(' ')))

def enc_byte(b):
    sensor_vals = ''
    bit_encs = []
    for bit in format(b, '08b'):
        seed = int.from_bytes(os.urandom(8), sys.byteorder)
        sensor_val = enc_bit(bit, seed)
        sensor_vals += ''.join(sensor_val.split(' '))
        bit_encs.append((bit, seed))
    sensor_vals = list(sensor_vals)
    for i in range(8):
        sensor_vals[i * 6 + bit_idxs[i]] = '?'
    return ''.join(sensor_vals), bit_encs

def rand_bit_flip(qc, main, seed):
    if seed % 3 == 0:
        qc.x(main[seed % 7])
    elif seed % 3 == 1:
        qc.z(main[seed % 7])

def enc_bit(bit, seed):
    main = QuantumRegister(7)
    anc_x = QuantumRegister(3)
    anc_z = QuantumRegister(3)
    syn_x = ClassicalRegister(3)
    syn_z = ClassicalRegister(3)

    qc = QuantumCircuit(main, anc_x, anc_z, syn_x, syn_z)

    if bit == '1':
        qc.initialize([0, 1], main[6])

    for i in range(3):
        qc.h(main[i])

    qc.cx(main[6], main[3])
    qc.cx(main[6], main[4])

    for idx in [3,4,5]:
        qc.cx(main[0], main[idx])

    for idx in [3,5,6]:
        qc.cx(main[1], main[idx])

    for idx in [4,5,6]:
        qc.cx(main[2], main[idx])

    rand_bit_flip(qc, main, seed)

    qc.h(anc_x)
    qc.h(anc_z)


    norms = [[1, 0, 0, 1, 1, 1, 0],
             [0, 1, 0, 1, 0, 1, 1],
             [0, 0, 1, 0, 1, 1, 1]]

    for i in range(3):
        for j in range(len(norms[i])):
            if norms[i][j] == 1:
                qc.cx(anc_x[i], main[j])
                qc.cz(anc_z[i], main[j])

    qc.h(anc_x)
    qc.h(anc_z)
    qc.measure(anc_x, syn_x)
    qc.measure(anc_z, syn_z)

    cc = transpile(qc, sv_sim)
    result = sv_sim.run(cc).result()
    sv = [*result.get_counts()][0]
    return sv

def run_insts(qc, main, res, insts):
    for inst in insts:
        toks = inst.split(' ')
        if len(toks) < 2 or len(toks) > 3:
            continue
        arg1 = res if toks[1] == 'r' else main[int(toks[1])]
        if len(toks) == 3:
            arg2 = res if toks[2] == 'r' else main[int(toks[2])]
        if toks[0] == 'x':
            qc.x(arg1)
        elif toks[0] == 'y':
            qc.y(arg1)
        elif toks[0] == 'z':
            qc.z(arg1)
        elif toks[0] == 'h':
            qc.h(arg1)
        elif toks[0] == 'cx':
            qc.cx(arg1, arg2)
        elif toks[0] == 'cy':
            qc.cy(arg1, arg2)
        elif toks[0] == 'cz':
            qc.cz(arg1, arg2)
        else:
            exit()

def measure_bit(bit, seed, insts):
    main = QuantumRegister(7)
    res = QuantumRegister(1)
    ans = ClassicalRegister(1)
    anc_x = QuantumRegister(3)
    anc_z = QuantumRegister(3)
    syn_x = ClassicalRegister(3)
    syn_z = ClassicalRegister(3)

    qc = QuantumCircuit(main, res, ans, anc_x, anc_z, syn_x, syn_z)

    if bit == '1':
        qc.initialize([0, 1], main[6])

    for i in range(3):
        qc.h(main[i])

    qc.cx(main[6], main[3])
    qc.cx(main[6], main[4])

    for idx in [3,4,5]:
        qc.cx(main[0], main[idx])

    for idx in [3,5,6]:
        qc.cx(main[1], main[idx])

    for idx in [4,5,6]:
        qc.cx(main[2], main[idx])

    rand_bit_flip(qc, main, seed)

    qc.h(anc_x)
    qc.h(anc_z)

    norms = [[1, 0, 0, 1, 1, 1, 0],
             [0, 1, 0, 1, 0, 1, 1],
             [0, 0, 1, 0, 1, 1, 1]]

    for i in range(3):
        for j in range(len(norms[i])):
            if norms[i][j] == 1:
                qc.cx(anc_x[i], main[j])
                qc.cz(anc_z[i], main[j])

    qc.h(anc_x)
    qc.h(anc_z)
    qc.measure(anc_x, syn_x)
    qc.measure(anc_z, syn_z)

    run_insts(qc, main, res, insts)

    qc.measure(res, ans)

    cc = transpile(qc, sv_sim)
    result = sv_sim.run(cc).result()
    sv = [*result.get_counts()][0]
    return sv[-1]

print("Here's your flag:", binascii.hexlify(cipher.encrypt(flag.encode())))
print("Alright, good luck decoding.")
for b in key:
    sens, bits = enc_byte(b)
    print('Sensor measurements:', sens)
    insts = []
    print('Help me decode, one bit per line, instructions (ex. x 1, z 2) separated by semicolons:')  
    print('You can only touch main or res. Use an integer to index main, or r for res.')
    for _ in range(len(bits)):
        inst_set = input('').split(';')
        insts.append(inst_set)
    bit_ans = ''
    print(insts)
    for i in range(len(bits)):
        bit, seed = bits[i]
        bit_ans += measure_bit(bit, seed, insts[i])
    print('Your byte:', bit_ans)
    print('On to the next byte!')

The challenge server generates a random 16-byte AES key to encrypt the flag. We are given the ciphertext, and then the server uses a quantum circuit to encode each bit of the AES key. We are allowed to get some measurements and add instructions to the circuit afterwards so that we can try to guess each bit of the AES key.

Source code analysis

Here’s the encrypted flag:

# ...

from Crypto.Cipher import AES
from flag import flag

key = os.urandom(16)
cipher = AES.new(key, AES.MODE_ECB)

# ...

print("Here's your flag:", binascii.hexlify(cipher.encrypt(flag.encode())))  
print("Alright, good luck decoding.")

# ...

Then, we must enter some measurements indices that we want to “hide”:

sv_sim = AerSimulator(method="statevector")
bit_idxs = list(map(int, input('Select a sensor index to remove from each bit: ').split(' ')))  

def enc_byte(b):
    sensor_vals = ''
    bit_encs = []
    for bit in format(b, '08b'):
        seed = int.from_bytes(os.urandom(8), sys.byteorder)
        sensor_val = enc_bit(bit, seed)
        sensor_vals += ''.join(sensor_val.split(' '))
        bit_encs.append((bit, seed))
    sensor_vals = list(sensor_vals)
    for i in range(8):
        sensor_vals[i * 6 + bit_idxs[i]] = '?'
    return ''.join(sensor_vals), bit_encs

During the initial steps of the challenge resolution, I didn’t understand what was this for. Then, I realized that each byte of the AES key is encoded separately, and then each of the 8 bits is encoded separately as well. The thing is that, on each quantum circuit, there will be 6 qbits that act as “sensors”, and the server will measure these qbits. However, we are told to hide one of these measurements.

Each of the 6 measurements for each bit is then concatenated to the next 6 measurements of the next bit, and so on and so forth. After that, the server will replace the chosen indices with a ? mark. Due to the format of the measurements output, I was smarter than the server and managed to hide a single measurement for all 48 measurements ($6 \times 8$) using:

0 -6 -12 -18 -24 -30 -36 -42

The above payload tricks the for loop to overwrite always the very first measurement by a ?.

Moreover, the server will compute a random seed and use it to encode the bit on the quantum circuit. Then, we will be given the measurements of the sensors.

Bit encoding

For each bit, a new quantum circuit is generated with this function:

def enc_bit(bit, seed):
    main = QuantumRegister(7)
    anc_x = QuantumRegister(3)
    anc_z = QuantumRegister(3)
    syn_x = ClassicalRegister(3)
    syn_z = ClassicalRegister(3)

    qc = QuantumCircuit(main, anc_x, anc_z, syn_x, syn_z)  

    if bit == '1':
        qc.initialize([0, 1], main[6])

    for i in range(3):
        qc.h(main[i])

    qc.cx(main[6], main[3])
    qc.cx(main[6], main[4])

    for idx in [3,4,5]:
        qc.cx(main[0], main[idx])

    for idx in [3,5,6]:
        qc.cx(main[1], main[idx])

    for idx in [4,5,6]:
        qc.cx(main[2], main[idx])

    rand_bit_flip(qc, main, seed)

    qc.h(anc_x)
    qc.h(anc_z)


    norms = [[1, 0, 0, 1, 1, 1, 0],
             [0, 1, 0, 1, 0, 1, 1],
             [0, 0, 1, 0, 1, 1, 1]]

    for i in range(3):
        for j in range(len(norms[i])):
            if norms[i][j] == 1:
                qc.cx(anc_x[i], main[j])
                qc.cz(anc_z[i], main[j])

    qc.h(anc_x)
    qc.h(anc_z)
    qc.measure(anc_x, syn_x)
    qc.measure(anc_z, syn_z)

    cc = transpile(qc, sv_sim)
    result = sv_sim.run(cc).result()
    sv = [*result.get_counts()][0]
    return sv

It looks scary, and it is! In brief, we have a quantum circuit with 7 qbits named main, then 3 qbits named anc_x and 3 qbits named anc_z. There are also classical registers to store the measurements of anc_x and anc_z.

The only thing that changes between encoding a 0 bit or a 1 bit is that the qbit main[6] is initialized at $\ket{0}$ or at $\ket{1}$, respectively.

The circuit comprises a lot of quantum gates, mainly Hadamard gates, controlled-X and controlled-Z between the main qbits. After that, a random bit-flip occurs, which depends on the seed:

def rand_bit_flip(qc, main, seed):  
    if seed % 3 == 0:
        qc.x(main[seed % 7])
    elif seed % 3 == 1:
        qc.z(main[seed % 7])

This function adds an X gate or a Z gate to one of the qbits of main. As can be seen, there are 21 possible cases ($3 \times 7$), although 7 of them (seed % 3 == 2) are equivalent (no bit-flip at all).

After the bit-flip, some gates are applied between anc_x, anc_z and main. The server measures anc_x and anc_z and outputs the results as a 6-bit string. Once all 8 bits of one byte are completed, we receive the 48-bit string of the measurements (with ? marks on hidden ones):

for b in key:
    sens, bits = enc_byte(b)
    print('Sensor measurements:', sens)
    insts = []
    print('Help me decode, one bit per line, instructions (ex. x 1, z 2) separated by semicolons:')  
    print('You can only touch main or res. Use an integer to index main, or r for res.')
    for _ in range(len(bits)):
        inst_set = input('').split(';')
        insts.append(inst_set)
    bit_ans = ''
    print(insts)
    for i in range(len(bits)):
        bit, seed = bits[i]
        bit_ans += measure_bit(bit, seed, insts[i])
    print('Your byte:', bit_ans)
    print('On to the next byte!')

Next, we are allowed to add more gates to the circuit and have an additional measurement, using measure_bit:

def measure_bit(bit, seed, insts):
    main = QuantumRegister(7)
    res = QuantumRegister(1)
    ans = ClassicalRegister(1)
    anc_x = QuantumRegister(3)
    anc_z = QuantumRegister(3)
    syn_x = ClassicalRegister(3)
    syn_z = ClassicalRegister(3)

    qc = QuantumCircuit(main, res, ans, anc_x, anc_z, syn_x, syn_z)  

    if bit == '1':
        qc.initialize([0, 1], main[6])

    for i in range(3):
        qc.h(main[i])

    qc.cx(main[6], main[3])
    qc.cx(main[6], main[4])

    for idx in [3,4,5]:
        qc.cx(main[0], main[idx])

    for idx in [3,5,6]:
        qc.cx(main[1], main[idx])

    for idx in [4,5,6]:
        qc.cx(main[2], main[idx])

    rand_bit_flip(qc, main, seed)

    qc.h(anc_x)
    qc.h(anc_z)

    norms = [[1, 0, 0, 1, 1, 1, 0],
             [0, 1, 0, 1, 0, 1, 1],
             [0, 0, 1, 0, 1, 1, 1]]

    for i in range(3):
        for j in range(len(norms[i])):
            if norms[i][j] == 1:
                qc.cx(anc_x[i], main[j])
                qc.cz(anc_z[i], main[j])

    qc.h(anc_x)
    qc.h(anc_z)
    qc.measure(anc_x, syn_x)
    qc.measure(anc_z, syn_z)

    run_insts(qc, main, res, insts)

    qc.measure(res, ans)

    cc = transpile(qc, sv_sim)
    result = sv_sim.run(cc).result()
    sv = [*result.get_counts()][0]
    return sv[-1]

This function generates the same quantum circuit as enc_bit, but using an additional qbit res and classical register to measure such qbit at the end. The circuit is initialized as before and uses the same seed for rand_bit_flip. Also, the same 6 measurements are made on anc_x and anc_z. Is here where we are allowed to add quantum gates between main and res qbits before measuring qbit res.

The gates we are allowed to use are these:

  • Pauli gates (X, Y, Z)
  • Controlled gates (CX, CY, CZ)
  • Hadamard gate (H)
def run_insts(qc, main, res, insts):
    for inst in insts:
        toks = inst.split(' ')
        if len(toks) < 2 or len(toks) > 3:
            continue
        arg1 = res if toks[1] == 'r' else main[int(toks[1])]
        if len(toks) == 3:
            arg2 = res if toks[2] == 'r' else main[int(toks[2])]  
        if toks[0] == 'x':
            qc.x(arg1)
        elif toks[0] == 'y':
            qc.y(arg1)
        elif toks[0] == 'z':
            qc.z(arg1)
        elif toks[0] == 'h':
            qc.h(arg1)
        elif toks[0] == 'cx':
            qc.cx(arg1, arg2)
        elif toks[0] == 'cy':
            qc.cy(arg1, arg2)
        elif toks[0] == 'cz':
            qc.cz(arg1, arg2)
        else:
            exit()

So, with all these, we must find a way to determine whether the quantum circuit was initialized with main[6] set to $\ket{0}$ or $\ket{1}$ in order to get the bits of the AES key.

Background

This challenge needs some knowledge about quantum computing. I’m not probably prepared to write rigorous quantum stuff here yet, but I can list some resources that helped me to understand these concepts:

I will try to express some key concepts in case you don’t want to dive into the above links:

  • In quantum computing, qbits don’t have a certain value, they have a superposition state. It means that they can have any value, until the qbit is measured. Once a qbit is observed, it collapses to a value (0 or 1) and it cannot be changed. And this happens with some probability, that can be expressed as $\ket{\psi} = \alpha \cdot \ket{0} + \beta \cdot \ket{1}$, where $|\alpha|^2$ and $|\beta|^2$ represent the probability of collapsing to 0 or 1, thus $|\alpha|^2 + |\beta|^2 = 1$

  • A Hadamard gate (H) produces a “change of basis”:

    • $H \ket{0} = \displaystyle\frac{1}{\sqrt{2}} \big(\ket{0} + \ket{1}\big) \equiv \ket{+}$

    • $H \ket{1} = \displaystyle\frac{1}{\sqrt{2}} \big(\ket{0} - \ket{1}\big) \equiv \ket{-}$

  • Measuring a qbit that has been transformed by a Hadamard gate has 50% chance of collapsing to 0 or 1

  • Pauli gates (X, Y, Z) behave as follows:

    • $X \ket{\psi} = X(\alpha \cdot \ket{0} + \beta \cdot \ket{1}) = \beta \cdot \ket{0} + \alpha \cdot \ket{1}$

    • $Y \ket{\psi} = Y(\alpha \cdot \ket{0} + \beta \cdot \ket{1}) = - \mathrm{i} \cdot \beta \cdot \ket{0} + \mathrm{i} \cdot \alpha \cdot \ket{1}$

    • $Z \ket{\psi} = Z(\alpha \cdot \ket{0} + \beta \cdot \ket{1}) = \alpha \cdot \ket{0} - \beta \cdot \ket{1}$

  • Controlled gates (CX, CY, CZ) involve two qbits: the control and the target qbit. If the control qbit is $\ket{1}$ the operation (X, Y or Z) is performed on the target qbit.

  • One direct application of the CX gate (also known as CNOT) is the Bell state, which is a form of quantum enganglement:

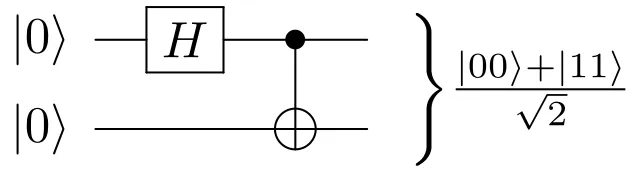
two-wrongs 1

The previous circuit has 3 different states:

  • Initial state: $\ket{0} \otimes \ket{0} \equiv \ket{00}$

  • After the H gate: $(H \ket{0}) \otimes \ket{0} = \left(\displaystyle\frac{\ket{0} + \ket{1}}{\sqrt{2}} \right) \otimes \ket{0} = \displaystyle\frac{\ket{00} + \ket{10}}{\sqrt{2}}$

  • After the CNOT gate: $\mathrm{CNOT} \left(\displaystyle\frac{\ket{00} + \ket{10}}{\sqrt{2}}\right) = \displaystyle\frac{\ket{00} + \ket{11}}{\sqrt{2}} \equiv \ket{\Phi^+}$

At this point, both qbits are entangled, which means that if we measure a 0 on the first qbit, the second qbit will have a 0 as well. The same happens for a value of 1. Both qbits will collapse to the same state.

Solution

In the end, my solution didn’t require a lot of knowledge about quantum computing. Instead, what I did was to find patterns by dynamically testing the given circuit.

Indeed the circuits generated by enc_bit and measure_bit are very complex to analyze them by hand. This is an example for a circuit encoding a 1 bit with a seed that is 15 modulo $3 \times 7$:

               ┌───┐                                          ┌───┐
q254_0: ───────┤ H ├──────────────■────■─────────■────────────┤ X ├───────────■────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────  
               ├───┤              │    │         │            └─┬─┘     ┌───┐ │                           ┌───┐                                                           ┌───┐
q254_1: ───────┤ H ├──────────────┼────┼────■────┼─────────■────┼────■──┤ X ├─┼───────────────────────────┤ X ├─────────■─────────────────────────────────────────────────┤ X ├────────────────────────────────
               ├───┤              │    │    │    │         │    │    │  └───┘ │                           └─┬─┘┌───┐    │                                                 └─┬─┘                ┌───┐
q254_2: ───────┤ H ├──────────────┼────┼────┼────┼────■────┼────┼────┼────■───┼────────■────────────────────┼──┤ X ├────┼───────■───────────────────────────────────────────┼──────────────────┤ X ├───────────
               └───┘       ┌───┐┌─┴─┐  │  ┌─┴─┐  │    │    │    │    │    │   │ ┌───┐  │                    │  └─┬─┘    │ ┌───┐ │                                           │                  └─┬─┘
q254_3: ───────────────────┤ X ├┤ X ├──┼──┤ X ├──┼────┼────┼────┼────┼────┼───┼─┤ X ├──┼───■────────────────┼────┼──────┼─┤ X ├─┼────────────■──────────────────────────────┼────────────────────┼─────────────
                           └─┬─┘├───┤┌─┴─┐└───┘  │  ┌─┴─┐  │    │    │    │   │ └─┬─┘  │   │ ┌───┐          │    │      │ └─┬─┘ │ ┌───┐      │                              │                    │
q254_4: ─────────────────────┼──┤ X ├┤ X ├───────┼──┤ X ├──┼────┼────┼────┼───┼───┼────┼───┼─┤ X ├─■────────┼────┼──────┼───┼───┼─┤ X ├──────┼───────■──────────────────────┼────────────────────┼─────────────
                             │  └─┬─┘└───┘     ┌─┴─┐└───┘┌─┴─┐  │    │  ┌─┴─┐ │   │    │   │ └─┬─┘ │ ┌───┐  │    │      │   │   │ └─┬─┘      │ ┌───┐ │               ┌───┐  │                    │
q254_5: ─────────────────────┼────┼────────────┤ X ├─────┤ X ├──┼────┼──┤ X ├─┼───┼────┼───┼───┼───┼─┤ X ├──┼────┼───■──┼───┼───┼───┼────────┼─┤ X ├─┼─────■─────────┤ X ├──┼───■────────────────┼─────────────
        ┌─────────────────┐  │    │            └───┘     └───┘  │  ┌─┴─┐└───┘ │   │  ┌─┴─┐ │   │   │ └─┬─┘  │    │   │  │   │   │   │        │ └─┬─┘ │     │ ┌───┐   └─┬─┘  │   │ ┌───┐          │
q254_6: ┤ Initialize(0,1) ├──■────■─────────────────────────────┼──┤ X ├──────┼───┼──┤ X ├─┼───┼───┼───┼────┼────┼───┼──┼───┼───┼───┼────────┼───┼───┼─────┼─┤ X ├─■───┼────┼───┼─┤ X ├──────■───┼─────────────
        └──────┬───┬──────┘                                     │  └───┘      │   │  └───┘ │   │   │   │    │    │   │  │   │   │   │  ┌───┐ │   │   │ ┌─┐ │ └─┬─┘ │   │    │   │ └─┬─┘      │   │
q255_0: ───────┤ H ├────────────────────────────────────────────■─────────────┼───■────────┼───■───┼───■────┼────┼───┼──┼───┼───┼───┼──┤ H ├─┼───┼───┼─┤M├─┼───┼───┼───┼────┼───┼───┼────────┼───┼─────────────
               ├───┤                                                          │            │       │        │    │   │  │   │   │   │  └───┘ │   │   │ └╥┘ │   │   │   │    │   │   │  ┌───┐ │   │  ┌─┐
q255_1: ───────┤ H ├──────────────────────────────────────────────────────────┼────────────┼───────┼────────■────┼───┼──┼───■───┼───┼────────┼───■───┼──╫──┼───■───┼───┼────■───┼───┼──┤ H ├─┼───┼──┤M├────────
               ├───┤                                                          │            │       │             │   │  │       │   │        │       │  ║  │       │   │        │   │  └───┘ │   │  └╥┘┌───┐┌─┐
q255_2: ───────┤ H ├──────────────────────────────────────────────────────────┼────────────┼───────┼─────────────■───┼──┼───────┼───■────────┼───────┼──╫──┼───────┼───■────────┼───■────────┼───■───╫─┤ H ├┤M├
               ├───┤                                                          │            │       │                 │  │ ┌───┐ │  ┌─┐       │       │  ║  │       │            │            │       ║ └───┘└╥┘
q256_0: ───────┤ H ├──────────────────────────────────────────────────────────■────────────■───────■─────────────────■──┼─┤ H ├─┼──┤M├───────┼───────┼──╫──┼───────┼────────────┼────────────┼───────╫───────╫─
               ├───┤                                                                                                    │ └───┘ │  └╥┘       │       │  ║  │       │ ┌───┐ ┌─┐  │            │       ║       ║
q256_1: ───────┤ H ├────────────────────────────────────────────────────────────────────────────────────────────────────■───────┼───╫────────■───────┼──╫──■───────■─┤ H ├─┤M├──┼────────────┼───────╫───────╫─
               ├───┤                                                                                                            │   ║                │  ║            └───┘ └╥┘  │            │ ┌───┐ ║  ┌─┐  ║
q256_2: ───────┤ H ├────────────────────────────────────────────────────────────────────────────────────────────────────────────■───╫────────────────■──╫───────────────────╫───■────────────■─┤ H ├─╫──┤M├──╫─
               └───┘                                                                                                                ║                   ║                   ║                  └───┘ ║  └╥┘  ║
 c62: 3/════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╬═══════════════════╩═══════════════════╬════════════════════════╩═══╬═══╩═
                                                                                                                                    ║                   0                   ║                        1   ║   2
 c63: 3/════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╩═══════════════════════════════════════╩════════════════════════════╩═════
                                                                                                                                    0                                       1                            2

Actually, this is a quantum error correction circuit, but it is not that relevant for solving the challenge.

So, recall we have 21 possible seeds (we are considering modulo $3 \times 7$), although 7 of them are equivalent. Then, we have either bit 0 or bit 1. That gives us 42 cases. I used the following code to get these insights:

for seed in range(21):
    for bit in range(2):
        print(f'{bit = }; {seed = :2d}; enc = {enc_bit(str(bit), seed)}')  

$ python3 test.py
bit = 0; seed =  0; enc = 001 000  
bit = 1; seed =  0; enc = 001 000
bit = 0; seed =  1; enc = 000 010
bit = 1; seed =  1; enc = 000 010
bit = 0; seed =  2; enc = 000 000
bit = 1; seed =  2; enc = 000 000
bit = 0; seed =  3; enc = 011 000
bit = 1; seed =  3; enc = 011 000
bit = 0; seed =  4; enc = 000 101
bit = 1; seed =  4; enc = 000 101
bit = 0; seed =  5; enc = 000 000
bit = 1; seed =  5; enc = 000 000
bit = 0; seed =  6; enc = 110 000
bit = 1; seed =  6; enc = 110 000
bit = 0; seed =  7; enc = 000 001
bit = 1; seed =  7; enc = 000 001
bit = 0; seed =  8; enc = 000 000
bit = 1; seed =  8; enc = 000 000
bit = 0; seed =  9; enc = 100 000
bit = 1; seed =  9; enc = 100 000
bit = 0; seed = 10; enc = 000 011
bit = 1; seed = 10; enc = 000 011
bit = 0; seed = 11; enc = 000 000
bit = 1; seed = 11; enc = 000 000
bit = 0; seed = 12; enc = 111 000
bit = 1; seed = 12; enc = 111 000
bit = 0; seed = 13; enc = 000 110
bit = 1; seed = 13; enc = 000 110
bit = 0; seed = 14; enc = 000 000
bit = 1; seed = 14; enc = 000 000
bit = 0; seed = 15; enc = 010 000
bit = 1; seed = 15; enc = 010 000
bit = 0; seed = 16; enc = 000 100
bit = 1; seed = 16; enc = 000 100
bit = 0; seed = 17; enc = 000 000
bit = 1; seed = 17; enc = 000 000
bit = 0; seed = 18; enc = 101 000
bit = 1; seed = 18; enc = 101 000
bit = 0; seed = 19; enc = 000 111
bit = 1; seed = 19; enc = 000 111
bit = 0; seed = 20; enc = 000 000
bit = 1; seed = 20; enc = 000 000

As can be seen, the enc_bit output is always the same for each seed, no matter the encoded bit. Also, mind that there are no two equal outputs (except for seed % 3 == 2). As a result, if we are given a 6-bit string of measurements, we can directly know which seed was used for rand_bit_flip.

Recall that on each byte, we will be hiding one measurement (the first one). This means that we will have 50% chance of guessing the first bit correctly. Given the fact that the AES key composed of 16 bytes, we will end the solution with a 16-bit brute force.

Now, we must tell whether the initialization of main[6] was either $\ket{0}$ or $\ket{1}$. For this, we can use common sense. What if we “undo” the operations of the circuit? Surprisingly, it worked.

Notice that the anc_x and anc_z will be already measured, so we won’t need them at all. The approach to follow is to apply the inverse quantum gates in reverse order. This time, the inverse gates are the same gates (i.e. the inverse of CX is CX, the inverse of H is H…). Also, we must add the additional gate from rand_bit_flip, since we know the seed.

Finally, we will add a CX gate between main[6] (control) and res (target), so that if main[6] decodes to $\ket{0}$, we will have $\ket{0}$ in res; and if main[6] decodes to $\ket{1}$, it will act on res to have also $\ket{1}$.

Implementation

First of all, we connect to the challenge, take the encrypted flag and set the hidden measurements (with the previous trick):

io = get_process()

io.sendlineafter(b'Select a sensor index to remove from each bit: ', b'0 -6 -12 -18 -24 -30 -36 -42')  
io.recvuntil(b"Here's your flag: b'")
enc_flag = bytes.fromhex(io.recvuntilS(b"'", drop=True))

Then, we define the mapping between measurement outputs and additional gates of rand_bit_flip, using the format of run_insts (for 000000, there is no additional gate). We also define the list of gates in reverse order, with the ending CX between main[6] and res:

rands = {
    '000000': [],
    '001000': ['x 0'],  
    '000010': ['z 1'],
    '011000': ['x 3'],
    '000101': ['z 4'],
    '110000': ['x 6'],
    '000001': ['z 0'],
    '100000': ['x 2'],
    '000011': ['z 3'],
    '111000': ['x 5'],
    '000110': ['z 6'],
    '010000': ['x 1'],
    '000100': ['z 2'],
    '101000': ['x 4'],
    '000111': ['z 5'],
}

rev_insts = [
    'cx 2 6',
    'cx 2 5',
    'cx 2 4',
    'cx 1 6',
    'cx 1 5',
    'cx 1 3',
    'cx 0 5',
    'cx 0 4',
    'cx 0 3',
    'cx 6 4',
    'cx 6 3',
    'h 2',
    'h 1',
    'h 0',
    'cx 6 r',
]

Next, for each measurements of each of the 8 bits, we create the list of instructions and receive the measurement of res, which should be the state of main[6]:

key = bytearray()
prog = io.progress('Bytes')

for b in range(16):
    prog.status(f'{b + 1} / 16')
    io.recvuntil(b'Sensor measurements: ')
    all_sensors = io.recvlineS().strip().replace('?', '0')
    sensors = [all_sensors[i : i + 6] for i in range(0, 8 * 6, 6)]
    io.recvuntil(b'You can only touch main or res. Use an integer to index main, or r for res.\n')  

    for i in range(8):
        insts = ';'.join(rands[sensors[i]] + rev_insts).encode()
        io.sendline(insts)

    io.recvuntil(b'Your byte: ')
    key.append(int(io.recvlineS(), 2))

prog.success(f'16 / 16')
io.info(f'Almost {key = }')

Finally, we apply a 16-bit brute force on the most significant bit of each byte of the AES key until we get the flag:

for p in product(range(2), repeat=16):
    for i, b in enumerate(p):
        key[i] = (b << 7) | (key[i] & 0x7f)

    if b'corctf{' in (flag := AES.new(key, AES.MODE_ECB).decrypt(enc_flag)):  
        io.success(f'{key = }')
        io.success(f'Flag: {flag.decode()}')
        break

Flag

If we run the script, we will find the flag:

$ python3 solve.py be.ax 32422
[+] Opening connection to be.ax on port 32422: Done
[+] Starting local process '/usr/bin/bash': pid 358568
[*] Stopped process '/usr/bin/bash' (pid 358568)
[+] Bytes: 16 / 16
[*] Almost key = bytearray(b'5\xc8(f\xe4U\x88v\xd25\xc9\xa1F\xc6\xc8\x8c')  
[+] key = bytearray(b'5\xc8(\xe6\xe4U\x88v\xd25\xc9\xa1F\xc6\xc8\x8c')
[+] Flag: corctf{c0rr3ct_CORr3Ct!nG_9aenq}
[*] Closed connection to be.ax port 32422

The full script can be found in here: solve.py.