winter

5 minutes to read

We are given the Python source code of a server:

#!/usr/local/bin/python

import os
from hashlib import sha256

class Wots:
    def __init__(self, sk, vk):
        self.sk = sk
        self.vk = vk

    @classmethod
    def keygen(cls):
        sk = [os.urandom(32) for _ in range(32)]
        vk = [cls.hash(x, 256) for x in sk]
        return cls(sk, vk)

    @classmethod
    def hash(cls, x, n):
        for _ in range(n):
            x = sha256(x).digest()
        return x

    def sign(self, msg):
        m = self.hash(msg, 1)
        sig = b''.join([self.hash(x, 256 - n) for x, n in zip(self.sk, m)])  
        return sig

    def verify(self, msg, sig):
        chunks = [sig[i:i+32] for i in range(0, len(sig), 32)]
        m = self.hash(msg, 1)
        vk = [self.hash(x, n) for x, n in zip(chunks, m)]
        return self.vk == vk

if __name__ == '__main__':
    with open('flag.txt') as f:
        flag = f.read().strip()

    wots = Wots.keygen()

    msg1 = bytes.fromhex(input('give me a message (hex): '))
    sig1 = wots.sign(msg1)
    assert wots.verify(msg1, sig1)
    print('here is the signature (hex):', sig1.hex())

    msg2 = bytes.fromhex(input('give me a new message (hex): '))
    if msg1 == msg2:
        print('cheater!')
        exit()

    sig2 = bytes.fromhex(input('give me the signature (hex): '))
    if wots.verify(msg2, sig2):
        print(flag)
    else:
        print('nope')

Source code analysis

The server implements Winternitz One-Time Signature (WOTS), which is an asymmetric hash-based signature algorithm. The purpose of this challenge is to tell the server to sign a message and then forge a signature for a different message:

if __name__ == '__main__':
    with open('flag.txt') as f:
        flag = f.read().strip()

    wots = Wots.keygen()

    msg1 = bytes.fromhex(input('give me a message (hex): '))
    sig1 = wots.sign(msg1)
    assert wots.verify(msg1, sig1)
    print('here is the signature (hex):', sig1.hex())

    msg2 = bytes.fromhex(input('give me a new message (hex): '))  
    if msg1 == msg2:
        print('cheater!')
        exit()

    sig2 = bytes.fromhex(input('give me the signature (hex): '))
    if wots.verify(msg2, sig2):
        print(flag)
    else:
        print('nope')

The WOTS algorithm itself is correctly implemented. The problem here is that it is wrongly used, since it is “one-time”, so using the same private key to sign two different messages is not secure.

WOTS

Let’s review how WOTS works:

The private key is composed by 32 values, each of them being 32 random bytes. Let’s call the private key $[k_1, \dots, k_{32}]$
The public key is derived from the private key using an iterated SHA256 hash function, denoted by $H$. So, each $p_i = H^{(256)}(k_i)$ for $i \in \{1, \dots, 32\}$

Notice that $H^{(n)} = \underbrace{H \circ \dots \circ H}_{n \ \mathrm{times}}$.

We can represent the private/public keys setup as follows:

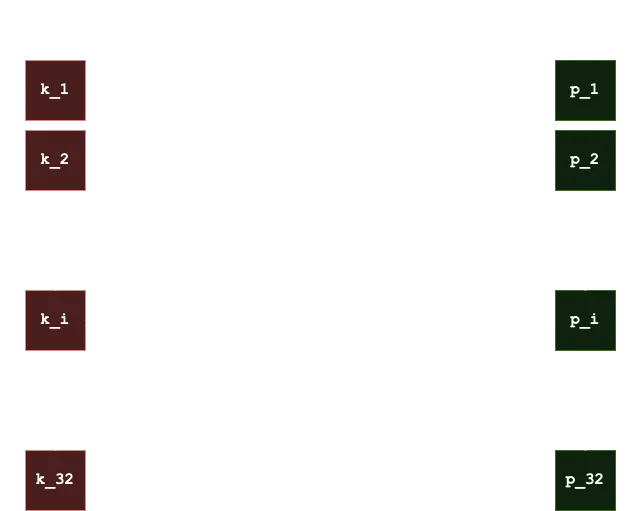
winter 1

Now, to sign a message, we need to take the SHA256 hash of the message as 32 bytes ($h_1$ to $h_{32}$). Next, we take each $k_i$ of the private key so that $s_i = H^{(256 - h_i)}(k_i)$. The list of $s_1$ up to $s_2$ is the signature of the message:

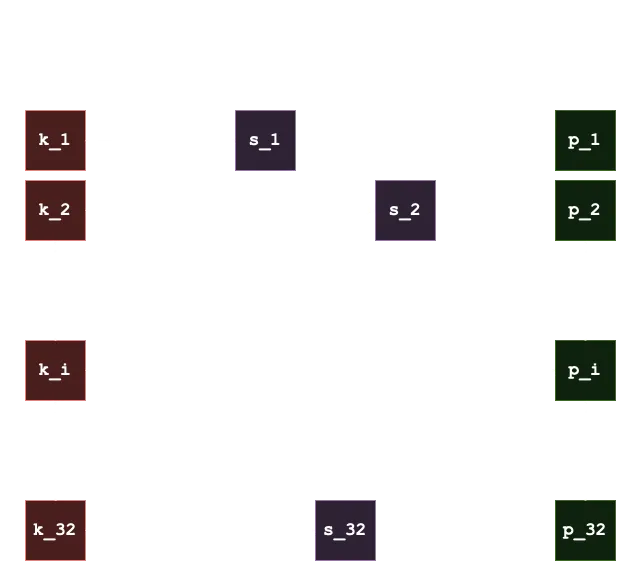
winter 2

Then, to verify that a message has a given signature, we take the SHA256 hash of the message as 32 bytes ($h_1$ to $h_{32}$) and test if each $p_i$ equals $H^{(h_i)}(s_i)$. If all 32 elements satisfy the condition, the signature is valid:

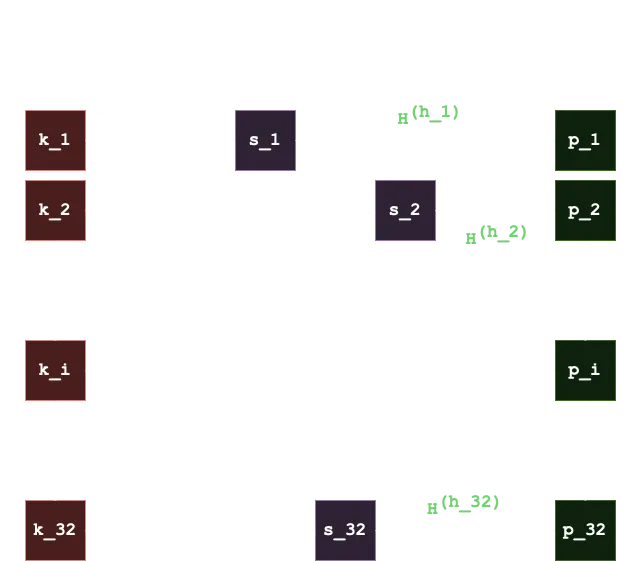
winter 3

Exploitation

The idea here is that if we have two messages whose SHA256 hashes satisfy that all bytes of the first hash are bigger than all bytes of the second hash (element-wise), then we are able to forge the signature for the second message by using the first signature:

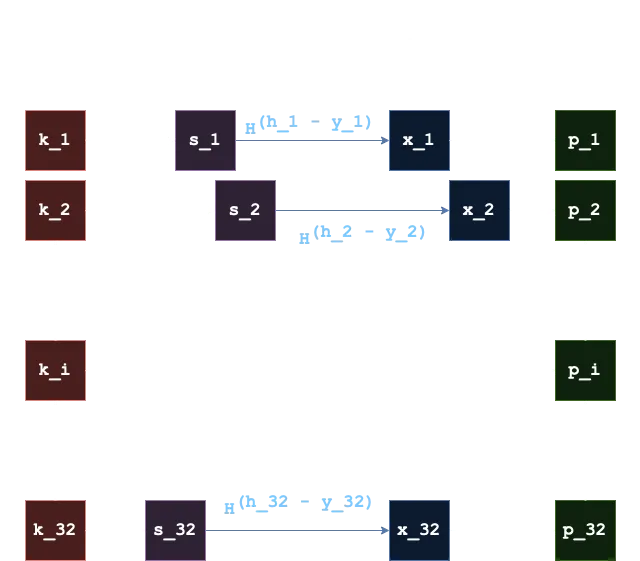
winter 4

If we find such messages, we will be able to forge a signature by hashing a number of times equal to the difference between the hash bytes.

Implementation

Instead of trying two random messages and testing if all the hash bytes are bigger than the others, I decided to use another approach. I generated random messages until I found one whose hash bytes are all greater than 0x80. Then, I found another message whose hash bytes are all less than 0x80. As a result, I have one messages whose hash bytes are all of them greater than the other message hash bytes:

$ python3 -q
>>> from hashlib import sha256
>>> import os
>>>
>>> while True:
...     msg = os.urandom(32)
...     h = sha256(msg).digest()
...     if all(hh >= 0x80 for hh in h):
...         break
>>> msg
b'\xa8\xf1\x16\xa4\xf6#sH|\xa4\xbbV\xc5\x08\xeaY\x1b\xc8\x0f\x9bbC:\x19\x0c\xd8i\x1d*\xa7M)'
>>>
>>>
>>> while True:
...     msg = os.urandom(32)
...     h = sha256(msg).digest()
...     if all(hh < 0x80 for hh in h):
...         break
>>> msg
b'C:\xe5\xf71\xec\xf7![n/\xaa\xed6\xbb\xdd\x14\xc8\xd6E\xb7\xc0\n}9\x19\x13\xd3g\x1a\x86\xc3'

With both messages, we can sign the first one (all hash bytes bigger than 0x80) and use the signature to forge the signature for the second message:

def sha256_n(msg, n):
    for _ in range(n):
        msg = sha256(msg).digest()
    return msg


msg1 = b'\xa8\xf1\x16\xa4\xf6#sH|\xa4\xbbV\xc5\x08\xeaY\x1b\xc8\x0f\x9bbC:\x19\x0c\xd8i\x1d*\xa7M)'
msg2 = b'C:\xe5\xf71\xec\xf7![n/\xaa\xed6\xbb\xdd\x14\xc8\xd6E\xb7\xc0\n}9\x19\x13\xd3g\x1a\x86\xc3'  

h1, h2 = sha256_n(msg1, 1), sha256_n(msg2, 1)
assert all(a > b for a, b in zip(h1, h2))

io = get_process()

io.sendlineafter(b'give me a message (hex): ', msg1.hex().encode())
io.recvuntil(b'here is the signature (hex): ')
sig1 = bytes.fromhex(io.recvline().decode())

sig2 = b''

for i in range(0, len(sig1), 32):
    sig2 += sha256_n(sig1[i: i + 32], h1[i // 32] - h2[i // 32])

io.sendlineafter(b'give me a new message (hex): ', msg2.hex().encode())
io.sendlineafter(b'give me the signature (hex): ', sig2.hex().encode())
io.success(io.recvline().decode())

Flag

With this, we can connect to the remote instance and get the flag:

$ python3 solve.py mc.ax 31001
[+] Opening connection to mc.ax on port 31001: Done  
[+] dice{according_to_geeksforgeeks}
[*] Closed connection to mc.ax port 31001

The full script can be found in here: solve.py.