<- HACKON CTF

El Reset de 1745

16 minutes to read

We are provided with a Python script that creates a private RSA key and gives us some additional information:

from Crypto.PublicKey import RSA
from Crypto.Util.number import getPrime,inverse
from sage.all import cos,floor,sqrt


def main():
    p = getPrime(1024)
    q = getPrime(1024)
    N = p*q
    print(N,q >> 450)
    print(cos(q >> 450).n(4096))
    # -0.83677025469083783941541701752761854754793836436580928644247008941810266469532458996045447348443859400152817824525738732652478723578550322419681449352934903962868272432839950443728133311767399079690030001079242722034971856216464693298008475334803612328029119715730610948114017183466860376219520135065944451843458471230390067711216822465611823803314088335568327990572989813880317949003496128817743756941657517592732976171161188449564836856703887590653409218974871687234942350215936871374265782174012360582549759635891009261305443677350659234691411334888094583016691447506478413851786692210332884103069291530840376504431016357464401672842279159473862600445695092589720790836314505433051945268839223026728538635526261735680020640125514694922387865117641745486767737807560114356069413145843513030254057578430063498955558945235100024577603060294061771113596755818633721728098654211982059793050427304804021628754473574523763161349682175284850419236582818156064980865716476145483816198034274679778084438576624517718459301374217997767985615596748052223448537502912453071556058736828589970943263917953424626006378389407199956646994682638376389500968564930356704561568053846692273026900362154710217069324829901876963571359354949212621973636284
    e = 0x10001
    priv = RSA.construct((p*q, e, inverse(e, (p - 1) * (q - 1))))
    with open("priv.pem",'wb') as f:
        f.write(priv.exportKey('PEM'))


if __name__ == '__main__':
    main()

In addition, we have a PCAP file with encrypted TLS 1.2 data:

El Reset de 1745 1

Although in the script we have a instruction print(N, q >> 450), we do not have this information. The decimal number that appears commented seems to be the result of cos(q >> 450).n(4096).

RSA

The public RSA key can be extracted from the PCAP during the TLS 1.2 negotiation:

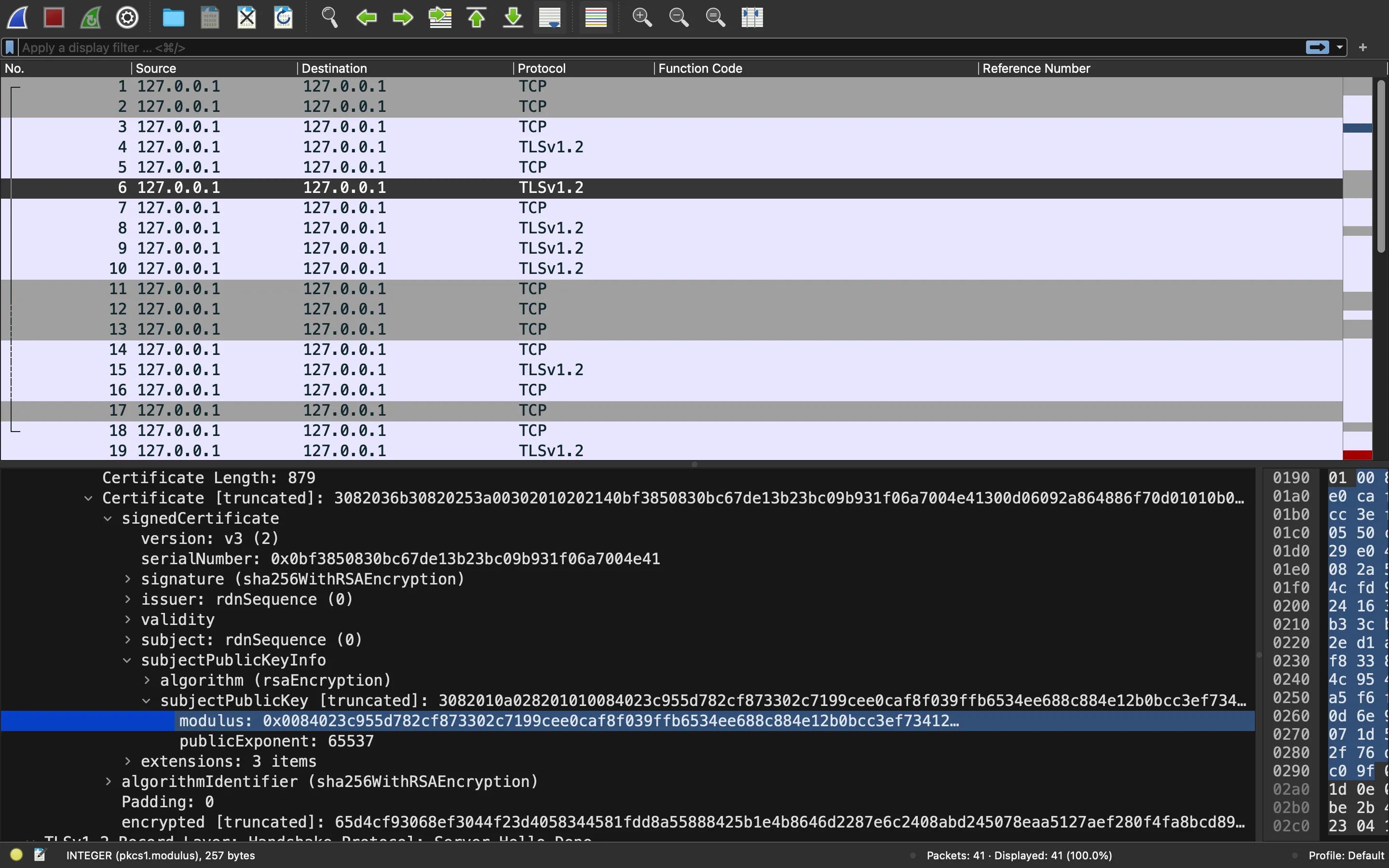
El Reset de 1745 2

Now, we need to obtain the private key (prime numbers and such that ) to decrypt communication. To do this, we could use the value of q >> 450, since with this we could apply the Coppersmith method to find . But for this, we need to obtain q >> 450 from cos(q >> 450).n(4096).

Integer linear relations

This part is very similar to the challenge Tan from ImaginaryCTF 2023. The only thing that changes is that the cosine is used instead of the tangent. The way to solve it is using a lattice and LLL to get a short vector.

We know that , and we want to find . On the one hand, we have many decimals of , and on the other, we know that is an integer. Cosine is a function , but inverse cosine is normally defined as . This is because the cosine function is periodic and only a period is taken as an image, by agreement:

Knowing this, we have the following:

This is an integer linear relation, which can be resolved by LLL. We can adapt the lattice proposed by the creator of the challenge Tan to our situation, where :

This way, we will be looking for the next short vector of the lattice:

In SageMath, this can be implemented as follows:

N = 0x0084023c955d782cf873302c7199cee0caf8f039ffb6534ee688c884e12b0bcc3ef734128a1a0253f0a878dc7abf060550cb695066686bcd52abba1227bd6f29e0422076ea9aadb4093346c321b16f082a579f467098fa6cf4f199abaa9c434cfd9bae44e08a689665ae223f9d9d12241637a083cdba46033a43674bb3704ab33cb930404171416a84a1fb2a55dfa12ed1ad939c4c37906affd81ee06c5602f8338a1dc958ea4d707f82c81132d4bd4c954f612ecad6633bc3b0d93905eacca5f6feacae5bb4210eb8ff74473253220d6e97d4e2ae9711c4b2ca3d2b1bd3b2071d5066f897ef909faab1a0f94f88be2f76d8bff6fbb1344c39257dfeea663ac09f

print(f'{hex(N) = }')
print(f'{int(N).bit_length() = }')

B = 4096
c = -0.83677025469083783941541701752761854754793836436580928644247008941810266469532458996045447348443859400152817824525738732652478723578550322419681449352934903962868272432839950443728133311767399079690030001079242722034971856216464693298008475334803612328029119715730610948114017183466860376219520135065944451843458471230390067711216822465611823803314088335568327990572989813880317949003496128817743756941657517592732976171161188449564836856703887590653409218974871687234942350215936871374265782174012360582549759635891009261305443677350659234691411334888094583016691447506478413851786692210332884103069291530840376504431016357464401672842279159473862600445695092589720790836314505433051945268839223026728538635526261735680020640125514694922387865117641745486767737807560114356069413145843513030254057578430063498955558945235100024577603060294061771113596755818633721728098654211982059793050427304804021628754473574523763161349682175284850419236582818156064980865716476145483816198034274679778084438576624517718459301374217997767985615596748052223448537502912453071556058736828589970943263917953424626006378389407199956646994682638376389500968564930356704561568053846692273026900362154710217069324829901876963571359354949212621973636284

ac = arccos(c)
pi_n = (2 * pi).n(B)

L = matrix(QQ, [[1, 0, 0], [ac, 1, ac], [pi_n, 0, pi_n]])
L[:, 0] *= 2 ** B
L = L.LLL()
L[:, 0] /= 2 ** B

qH = abs(round(L[0][-1])) << 450
assert c == cos(qH >> 450).n(B)
print(f'{hex(qH) = }')
print(f'{int(qH).bit_length() = }')

And with this we get the value of (q >> 450):

$ sage solve.sage
hex(N) = '0x84023c955d782cf873302c7199cee0caf8f039ffb6534ee688c884e12b0bcc3ef734128a1a0253f0a878dc7abf060550cb695066686bcd52abba1227bd6f29e0422076ea9aadb4093346c321b16f082a579f467098fa6cf4f199abaa9c434cfd9bae44e08a689665ae223f9d9d12241637a083cdba46033a43674bb3704ab33cb930404171416a84a1fb2a55dfa12ed1ad939c4c37906affd81ee06c5602f8338a1dc958ea4d707f82c81132d4bd4c954f612ecad6633bc3b0d93905eacca5f6feacae5bb4210eb8ff74473253220d6e97d4e2ae9711c4b2ca3d2b1bd3b2071d5066f897ef909faab1a0f94f88be2f76d8bff6fbb1344c39257dfeea663ac09f'
int(N).bit_length() = 2048
hex(qH) = '0xb1eb9278a603d830a202f0c2a46b9c97e0563d8e710948527e185e2f2b4fbba2564309f004bb2ca615b378f494c769890afc6c1f4e7c17c9aa88a8fe99214e3bc88b8d47d335d2700000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000'
int(qH).bit_length() = 1024

Coppersmith method

Now we can use the Coppersmith method to find the full value of , since we know some of its most significant bits. A similar challenge is Bank-er-smith.

Even so, it is not so easy to implement since we need to find 450 bits of a 1024-bit number. It is a rather small proportion to make Coppersmith method work well. For this reason, we can help the algorithm with a small brute force (up to 16 bits is affordable) and knowing that the least significant bit will always be (since the number is prime, and therefore, odd). We can also use different parameters (normally, around because ). Thus, the SageMath code remains as follows:

import itertools

P.<x> = PolynomialRing(Zmod(N))

for qq, beta in itertools.product(range(2 ** 11), [0.49, 0.499, 0.5, 0.501, 0.51]):
    qqH = qH + (qq << (450 - 11))
    roots = (1 + 2 * x + qqH).monic().small_roots(X=2 ** (450 - 11 - 1), beta=beta)

    if roots:
        q = int(1 + 2 * roots[0] + qqH)

        if N % q == 0 and 1 < q < N:
            print(f'{beta = }')
            print(f'{hex(q) = }')
            break

And when executing it, we get the value of :

$ sage solve.sage
hex(N) = '0x84023c955d782cf873302c7199cee0caf8f039ffb6534ee688c884e12b0bcc3ef734128a1a0253f0a878dc7abf060550cb695066686bcd52abba1227bd6f29e0422076ea9aadb4093346c321b16f082a579f467098fa6cf4f199abaa9c434cfd9bae44e08a689665ae223f9d9d12241637a083cdba46033a43674bb3704ab33cb930404171416a84a1fb2a55dfa12ed1ad939c4c37906affd81ee06c5602f8338a1dc958ea4d707f82c81132d4bd4c954f612ecad6633bc3b0d93905eacca5f6feacae5bb4210eb8ff74473253220d6e97d4e2ae9711c4b2ca3d2b1bd3b2071d5066f897ef909faab1a0f94f88be2f76d8bff6fbb1344c39257dfeea663ac09f'
int(N).bit_length() = 2048
hex(qH) = '0xb1eb9278a603d830a202f0c2a46b9c97e0563d8e710948527e185e2f2b4fbba2564309f004bb2ca615b378f494c769890afc6c1f4e7c17c9aa88a8fe99214e3bc88b8d47d335d2700000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000'
int(qH).bit_length() = 1024
beta = 0.490000000000000
hex(q) = '0xb1eb9278a603d830a202f0c2a46b9c97e0563d8e710948527e185e2f2b4fbba2564309f004bb2ca615b378f494c769890afc6c1f4e7c17c9aa88a8fe99214e3bc88b8d47d335d273853ffec0cf7b36bc4d3095ccec142bd53ef2e79ecb1ac926646beede6b327383ccd62af2908299c4ab193808281b330249f0fd4e7d92f4ff'

Great, now with this value of we can find the private RSA key and decrypt all the traffic of the Wireshark PCAP:

#!/usr/bin/env python3

from Crypto.PublicKey import RSA
from Crypto.Util.number import inverse, isPrime

n = 0x84023c955d782cf873302c7199cee0caf8f039ffb6534ee688c884e12b0bcc3ef734128a1a0253f0a878dc7abf060550cb695066686bcd52abba1227bd6f29e0422076ea9aadb4093346c321b16f082a579f467098fa6cf4f199abaa9c434cfd9bae44e08a689665ae223f9d9d12241637a083cdba46033a43674bb3704ab33cb930404171416a84a1fb2a55dfa12ed1ad939c4c37906affd81ee06c5602f8338a1dc958ea4d707f82c81132d4bd4c954f612ecad6633bc3b0d93905eacca5f6feacae5bb4210eb8ff74473253220d6e97d4e2ae9711c4b2ca3d2b1bd3b2071d5066f897ef909faab1a0f94f88be2f76d8bff6fbb1344c39257dfeea663ac09f
q = 0xb1eb9278a603d830a202f0c2a46b9c97e0563d8e710948527e185e2f2b4fbba2564309f004bb2ca615b378f494c769890afc6c1f4e7c17c9aa88a8fe99214e3bc88b8d47d335d273853ffec0cf7b36bc4d3095ccec142bd53ef2e79ecb1ac926646beede6b327383ccd62af2908299c4ab193808281b330249f0fd4e7d92f4ff

assert n % q == 0 and isPrime(q)

p = n // q
e = 0x10001
priv = RSA.construct((p * q, e, inverse(e, (p - 1) * (q - 1))))

with open('priv.pem','wb') as f:
    f.write(priv.exportKey('PEM'))

And with this file priv.pem We can see the PCAP traffic when importing the key in Wireshark: (Preferences… -> RSA keys). What we see is an HTTP request to /secrets.zip and its response:

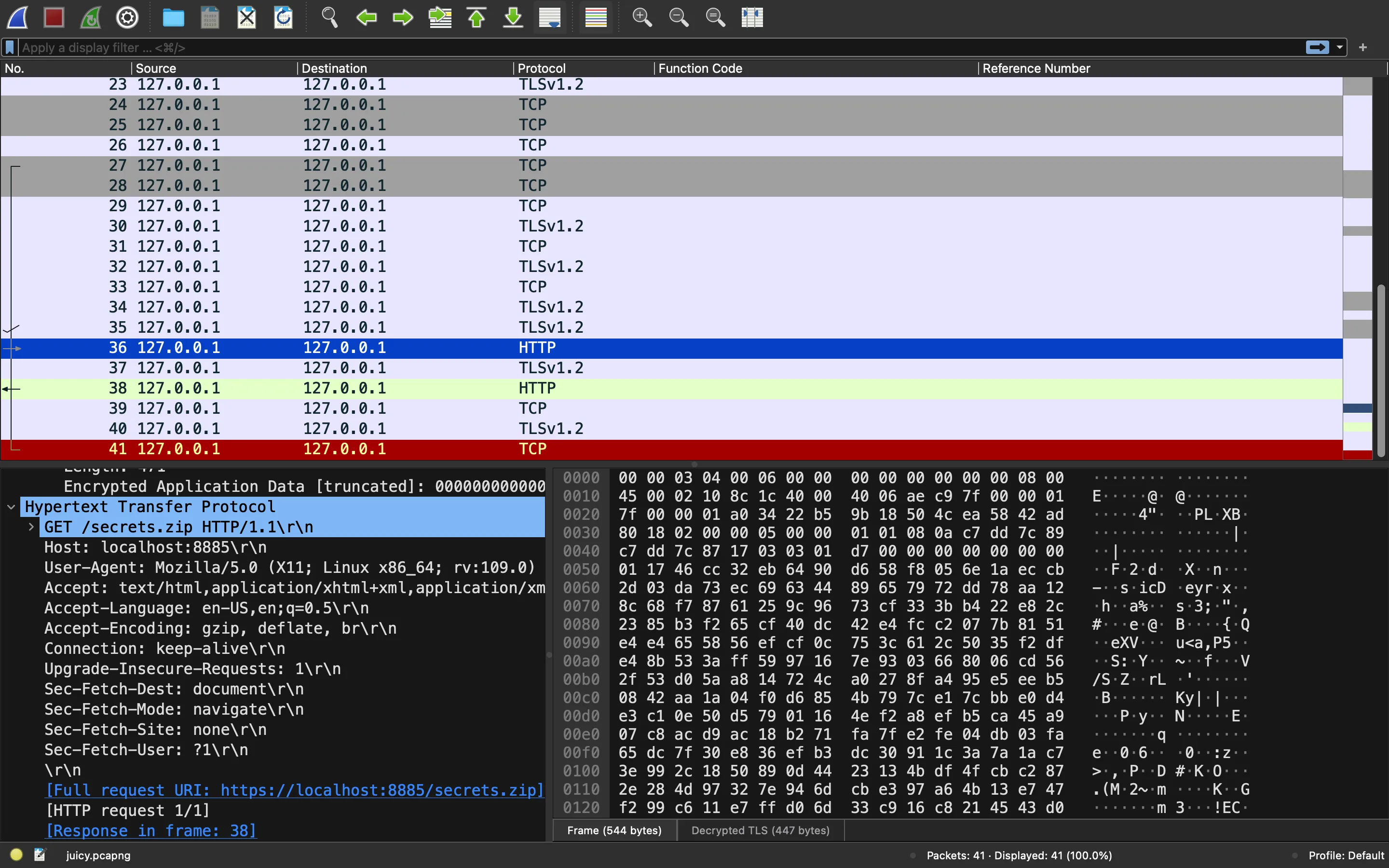
El Reset de 1745 3

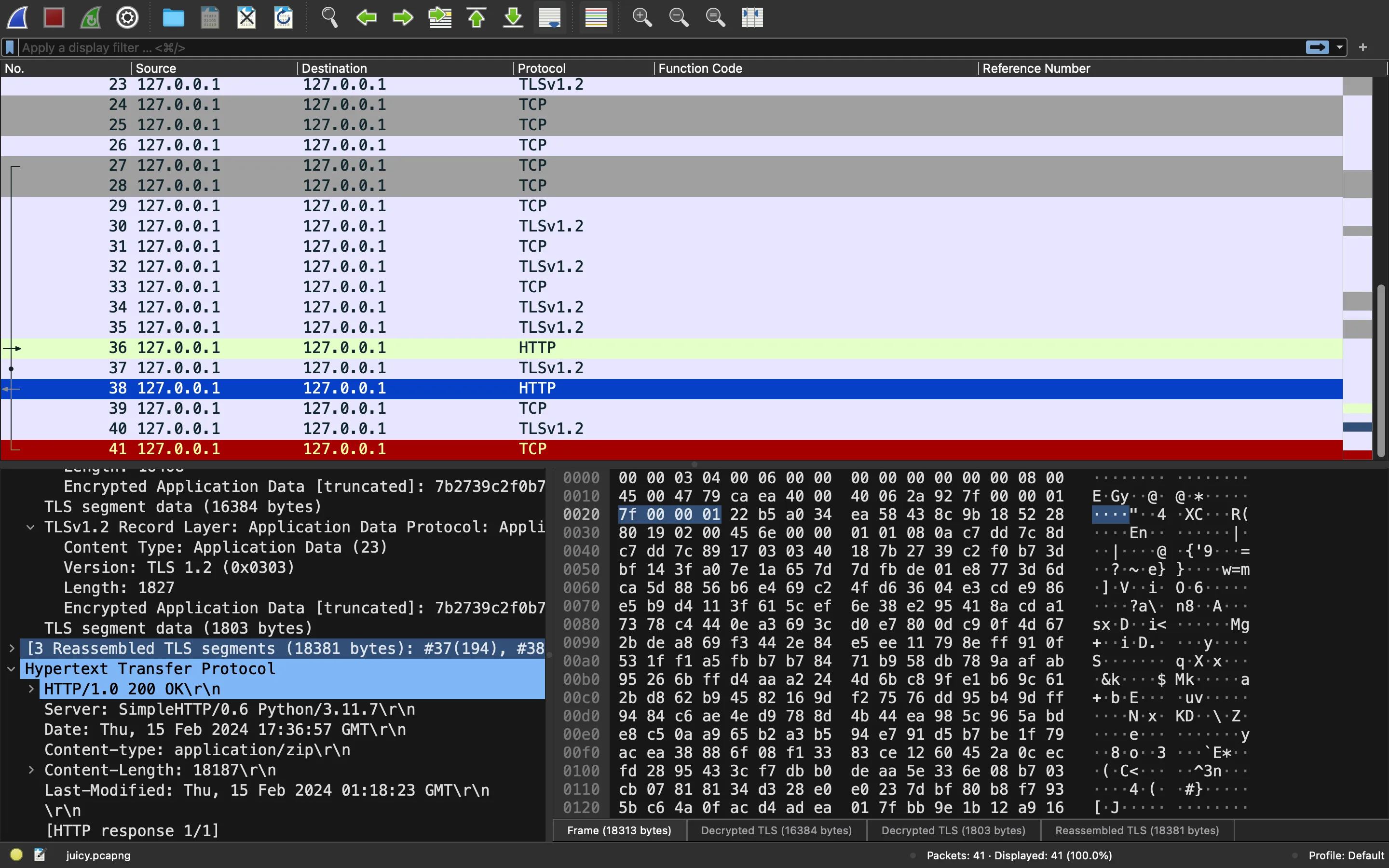
El Reset de 1745 4

ECC

By extracting the ZIP file and decompressing it, we discover two files:

  • chad_encryption.sage
from Crypto.Util.number import  getPrime
from Crypto.Util.Padding import pad
from Crypto.Cipher import AES
from hashlib import sha256

def hide_flag_between_reptilians(key,plaintext):
    iv = b"iseeyou!"*2
    cipher = AES.new(key, AES.MODE_CBC, iv)
    ciphertext = cipher.encrypt(pad(plaintext, 32))
    return ciphertext.hex()


def get_master_parameters():
    p = getPrime(431)
    q = getPrime(431)
    Gx, Gy = randrange(2**256,2**257), randrange(2**256,2**257)
    a = randint(2, (p*q)**2)
    b = (Gy**2 - Gx**3 - a*Gx) % (p*q)**2
    return (a,b,p,q,(Gx,Gy))


def third_dimension_ecc(G,N):
    garbage = [randint(1,N) for _ in range(32)]
    secret_array = [garbage[i] * G for i in range(32)]
    print(f"In your dimension you are able to see this: {[x.xy() for x in secret_array]}")
    return sha256(str(sum(garbage)).encode()).digest()


def main():
    a,b,p,q, G = get_master_parameters()
    N = p*q
    E = EllipticCurve(Zmod(N) , [a,b])
    B = E(G)
    master_eye = int(E.change_ring(GF(q)).order()*E.change_ring(GF(p)).order())
    point2inf = E(0,1,0)
    assert master_eye*B == point2inf
    print(f"The Master Eye is granted to you: {master_eye}")

    EM = EllipticCurve(Zmod(N**2) , [a,b])
    with open("flag.txt","rb") as f:
        FLAG = f.read()
    KEY = third_dimension_ecc(EM(G),N)
    print("enc_flag = ",hide_flag_between_reptilians(KEY, FLAG))
    

if __name__ == "__main__":
    main()
  • output.txt:
The Master Eye is granted to you: 16265471931640785828934127858946752538285468297743536678369884769655894080669562147795213991083005768993394358509783223221158858616114956533429224780974963093860223870869151381622793452378040102391285088110131930993214655276327069828109098832154854719776594644
In your dimension your are able to see this: [(79364468785236952279306319947486981248865881109689880151701940694064893979908366213038221679380344986127502056375006658490264731158574287241753313341555481402017633356285197771242603178001464846171145411665369899716221278004315749554836475575261046450436145959429152755593843874272934087644242937261243790850746058845526628319552492967085187705098606977143896792510184949161152227872504750529657542182084860998608178545130782929487362604009699589317802551001766633251821245604199207911871496973183520003360060704663214, 16687868136816790667937853246796901063040944936759940662722448380093920072006750947759005398743346758508016260528885932320663505212977936388527162162700995881129762284545953159504084714702981447856577155545734415853887630161403524590482445165827667785041932424914364528689537173920286382744504598070079197190571583803626137199250536574114579102857674775519365478519464262272039879237629974345129100337321029345797122618346654708409642719988452075056672175360303595214679844777756177806896404220841682828148652726672638), (18899724296709356965234494619104772779470606388931481117456688008818773207217366971633275128353972861633690819420635187472982517415400458909499316310931735946901572543121761179549512998697352800479852589929855627415400504246815106263800422957389670026191418168234235240406098997159721205877122915135525815565333680276051547563185321448352067894786538244048272702500927838999047658003300634824432270546232541050231457086443144424139179909585041352826454599094625605744436472796192783054911539407677446501812033471321524, 181969980377542764707955040897437722784709145520407120692028567222043813796008600849964806554297247610034947681294613264869782056823632123233711963621923181395296514822877676280308872426739819929410735010216364608798913264921312771916561066019134544296445889808932682039938044349353633612260789631107610936747968998606077205378127104320871869801486116872451256587440551053631039031230396157049192240149053601614033999746393390194723403360681914729802280523975083933174774134319246514382925460749896675407154805485284511), (68471692495575172133443182331265395323780023618521247524518268730711946951940988673749804251758452778660185511305483225416051708878357189530595965992350055334820378387109046064384283138464825854455750319884417034907809207922174034293151428401066968153603720309881678240489554389902246968911783683529409598893006732050710469464502354213081471824890463157409366264164051370265213326073053285020204917375631748764264712643374983681057721917952358757015432749432908948261428353275093151790075022197714189206163134215315103, 21086153520048598786169857750936805604277664567817774664460508684003670502302309090451996890460669084397056007859256108355293069289180286744069869788034455379356774892426063355812211938369687363613649187261276214647682224924760631173273646480179734923052819579729206566136998202738004693357079772445998313417118811575716713719713425456903643208635220241330814329516583323942979855886550421694669869092246154864251064889038193612822797937736925854371199646805580554872113726878535438082715356751200540213482107525098188), (116969053282694964799384771184091326303783633954428385196195106448482795095537983186445774516345149664381173834220871423555644858263622043970631708050194494865598220654365692163194726440427226462426292354441330021886333830775935143649055408074223466986424355324037704727682925776252702628182654864848940761049870226530117740598115594078111417658004448199672691637414626676511064717083418122102790469776547004932065495742273400807655050349768888802235266816179305399411904017010194674411837318963119660814179508659522079, 50084014889793959696599960870266488490551570031242416218275044365044406279560773812159187876069277424936558566002408934269450009685126762919422186537900216338665358746852202216630815904714706257229182538937888481607640416939802948615453184222442533517179199989078012953988190237579277262608278898391324918782630916840313135675473154777780855027523835253960743640206425166079504138147039127770593334045531030931479175201464964155413852798543401227075673058536367848947304461742267492110565792799164008125042863814750484), (75495634491380681480755034982641869190790206884849110723256175106318578661884367627647143036688535570791725909016139335131090112769001955747766299722705758599159778181042043453667346349033547319312262250475534057045860453347457133690528259902127083849168115417362595686165076571790325723969187880950829034560735006803713082244776521462470725461944018138446316622326672180314948459934243221388622927753353641287295474464745004329035876313365899195265984567422425276920658644349603345662940685219340306202950650607462424, 36253213840544424135747639984625468377126489352389007053380932532914480713717870396970116475077843047531097911732210943486983201258877192757861153015876591828621816348899115209925885000722027312971132000986223661591438360763777219039380763132328418089417368883034318747845529041436281909436209997433288486880452129344883136566180200589020934893263313246425182857484118510922258585583154053518563004163870433471783169696048347094801055344875002707558347225173012259302506287684325108055470698444963530011674895234940861), (192481455040907281329193584721852105461149835280168733847414582510382943795683937046047272270386155455427903029708072280124641608091666028101203441908633497627017890386867343567857125870268607159026410298301416630232047646360786504167687619545786494459446199856135388394976238012143847784593439590750118221999002429721920816932370398509030842536157171976181011006850034186822030054621552078384154095398615589672184024311433279726791936051360592141198012580769956217276136748224000824970866935881059774801322488495734737, 263750748030593406555372960075339347959501012664293859999528761406646617202885255209546013672103696519460696026989591318113562143370752757504971207850886357088200588529406714681418094672394611241767914354242709867737587173914012871284335033363056451884058022592279355794323391316627257591556094592398182461024352393825325635906355111844626491458756610991526543618068466546705753811183653095707925663763039824680079042497299645105323384745735490293862452599416389420082263130648481405274914126094178915535243279138216891), (255417412247910237204056992220045681879601415453288901101493272549214517912477637905405057604185717193019107588463580766046854561097661737623152334645649813648085887341524457445897093708191115078479102309838323390531754049310253939778322042103086681614882877414565503266734052030713798844268300288931266616639070681932489338231071158921404363210396384266907626544529764539182475404302001747080341642167481344327297753736338699702763493207235894318368979448459989566928583831763472499113910984819179772191593553652132474, 216838227007896475467505545385808596622593627839947735482086337073695133835970632571085739743178459369081219447146261545489025016023191480118835913846110397255114648919854819641700710717424878468620182038420695530305995881014362474635138548754798584240818513132332952780471786911557099270185846735324286244202698215309265097328428369735979500503151382847521451988517209863599729938833413473246217315543633075429285724935075345739203874313074322507039546739903067587047347937253792823522407423759267865629674811587336735), (124096126188514803544503955059315279141132559829237017973895020854171803237264834921222239856902238141179876125883968947274872965203378100360103207367714763024384163506879494701103972703086350129968586526203471429720871699511033522121952069111450022016969221035561423806264769591980121521115751553028030488337106779564554084983419507958422995036643408111208147569385927747112032878129152578402922719412406569384357851502035073976747328543651617464058989532223729123880689755690748865232003435467745311460600569632062195, 79795929489497405541344074279045484311257046279349845074266797064963552718105676350112801481079796697379543842277745402508713939382393071567528053085584437224203083580852710549037874369323959513137365714211165782436080036247333330794646390255560519641038629449067754438673314304868898813042624277285756041579001910407073190691633730020025977695329396764438605452385145610146775049817517456197497958984225616236669698260373850993781035376644766912592244717606326819474841714478055835222357317541164073792768197449976805), (190703286030345244045469778665561974216325069308265949202325894850227791765904139485525133899256922401602997366124011248349376295580261874319338852553684877393759367840644756984940510336404382711261363588684354508782828978401315935725937405785634244395621036683704621600788947421051146412108450650360926888325295167558040472336174751620673578392573280408257149796768348815768625550159870118878124609165630736159309639790673200547390682579251405402083531773765502679177847618650304506944498168089416322240738303940653213, 24736645903036881803140323581228716611113404998832076832196705758532168994501238783666375149022287321792427144500995307601858381136965807435697339506741211246927952932690067441621139167964194664193434621736623395830739730041951079386866340029257422408469503684333096054282304496745395068380277705022308880154716936569675145590997527120346373478094696152761116815474531993309298675688562696276172987521492269383043279810681588686656859154216730700730536263035848904078841458919347823245082214554180323650026964599193449), (258703341869999263552696566941924062917262532623427112981841289107534325684990395930426708646820618617158698098807584327410715882613007054798579382797202218924771823397597250874444158233109489433439437861168171982652882535734326225316450293623741694672869263741406310745286481287471748736505002599328297372513945104194558584930703398823479254727890496522036645921691948539312161687230707649623943993196786543478056821803577376429265789558098025007309268634834269286613805213473295723199595802084698720821452641690348762, 157597653185058333749305618814281541720926026316916248894515953007654834382945318302782897071081232168734135231503541126542944853455636669320882162239580132818141369909385380309951303769335111171767021649073648211864119796372073673232431330520655857858471659683744957380388861533423069333178715676730080139275594800569694523547635241524786097810950368839577943317787129038527925602633331544524871784599829599691035333266868107278941473293754170485781398238637499037126629714954539370303741202156428560403509971269120259), (144029484484143740842105007898750587818400259866067203106619661765763196612852225351180802281798132738759712673153837981988639932431947090809824592374750203985082077932231250238993558934126045641958929154545019638665302385408753639772238214965583998593458523982768916457289049350438036003586345084629417537221581589792274874386127526724174033010886505160380617273573415323932040916826340570542462697219927548091751481509377962625757071590735901774613456978510749747386546939521455040718702532592290387855298509964335504, 81136403803938509674953360140216723808828994157366853530661289992039975024693660530412770844694016294799917019166287093752795881772713038987632126846487124365054635128318325215698759027661009762825117366778570281270937841455064304807681267714958371425526732088357275832549199054044120705515004113312778633030563138690914909627177849996617456660673293755637236050697184282677574577668950305536160357560245868725179346462569085515282246946818804551864995963132631326540113293786152201453968620257820912842230789280672879), (167933423643310489968736909399339291074532111423728809018251315108934196550988975700904712999504968918797886060359964419385418362138089494181042173732835977776288115501526781854180140081384888294467362388183968192889440693933788263691009913440459578937986555297497010971816134549682779591167883513859028748417671900766328167176421597712058150529821656694452760283330487597721120507927015978002030880379686393503772683299429146980224934216236258524809257894318690697716404775604790364766740110823609354214543678454335207, 249060203030314638656800525340380123405021821952904721849953191711065909060250501335838898260047436743185888780451959829884660980671620355155805987888739105567254190879933334691411436378354628161756038668310804522041631705561214001778546633300265947270561795770260431256098931841216149131420253712922540548278872260455771972510899952597837538488876155123609496441312030794339392252544212884101476954780198469300130297678877552887865118112329028954549930740352455919380615142366214732987382847820614960930054016512403685), (81531132387261687911917499446685797723971871365375671509000262296850261719634523323876587160746818150479196876938791972820817931157649714415936984850766979784687364441837634119019081500667512591299111427780436432976950026422776044193795432616317613520986261395626116948865296824517463828639995464038528157308915881004595745408077589331144910923977821241124679034305505478460626044978730506369719002450030831539905895506531403799691784318024460051225878101146939170314725597099259252484920566074712476020128146708728763, 2937120054477468141509617584718072841466725665936920849977929083765990055665939440305887249811696047078394520908428092839293350858414170848178164083344045344698200810920746906003705786425990783693973403162815180341354385994880845699003303202234732248708097094724976024552659615350213712717065586514234121293071473763401980455740807740160917980173788010327993607060642470248510559196661609000914685808353954049312164318177565333183579224288193591968204930301057232213051631057654211493148123839424779942852687340685859), (103644260861603589957248808023254195447470005051473901151854421472615182158114771695576397034699248112789770191530282302797868406969984836822917079823398511974177377027477715431406825405053605595879747122357745078872754130028142971701445852516659874028185272404314555307882576155287855648800598012051775334174420913382203557539801927105317596120387809472648928484865311968302940472396169283793012693982543833931245644607885977240792560196956780193270009230312161519165925549238619384488289402663988278459288965755045202, 13386131823381627746769871412188175354099500837026101545007050182395652213622116827516458708885503040423176624137354534217799527216400345533053176835186505390864762712683850484524757574534628840609687178597044082451530395700669918033403997664280245962765624164711393899615828305969266729155003151307376498365166318455594869316786666702572444740194586528840860391405316667797716685898051306351300068423693781875048265594832229743511143553177543907602987672492835074752327279125873635511855999185175110114329459883377537), (49806447733446335028783340650616199033338438619086297731292629401023714767537877728133378993911023452403002227083159364255769432882774341778909294590221930944811276789872595855728949386605648638168750044129790208111103100331015942951240705120476205432357062176913813923085615505235799335479085172612638542586397849084541871749283790134400068035128471694535143019228346147248907280201471476695674163387417128954358898944253662151554055947196719426143186764729676220385474455614516558327773933799259609604596713816808540, 67153879925391225704783520063321728291841246303771866370802949117008384122412140630611604172020608684305418836497124227910945398307322662493354546743254952303151830473091638175848920166466803499511290396766988373587222642302671831397081157040791215851705427492378162911106643097070740607333182057088894418177665114567377267999038233912213229123903048082371574624240893841173078444693780515417133220692841998171028137554861232812549476624566311728736485760045414080572245456064999665273894920043788708634808692721225111), (121259199659160450418948388268391671626763025328320946113219792501668203928186402325839464256295141580273373580230405155605770463172239061805223622554363862547879300443826551552724595822125684018396490933825583005990724827277076614006784797779689099622702460506413009438350060304272340392268432807413132707604981714652259643802514139444520463112200299452118287602493071775805573055176357194744688372487796393645874066138755543916937978565303290845579555253269930091309454226581952736942651259771285494328313841696719176, 54423785383353167245475846055742639414462824811528992154255919783122213594530026632096607760980193960486608312853375968958284421107224238091920595029896291015596986820214401232689927476113723708035744569656886855911932772506245596347237606736702765609624147987779604630980992572618251242821548630723856294062865887942586987410202233110518443350460787360988488460220225272399530872204640419820350367837356650390876309151879191299124610782813723570535829463907264642390350356162471637889917462673983296700274587307954465), (92977303619726373774401333534444147442488907995426361498879182990025454415553018333510508171552601209120558825262326946206424684031961499092804928326240295304486879568678879403499951176191105736205078630584013388298255658637491139786884227468870908840259825869871138175305278010052511608139487753205231824362171703992332827590103700189042458984190221436070514094303300081382771155591123233515363366709552805738441658312586231620217316133963684195358526529253054377690560419819547756625965095265987708024421058924420032, 17534083239981379559980686853294607180922082121446077383464277173041051133747075976359326283052436801964963297772275562097872932301281868876431190065920949359745987270625836847527970947817991199732508451593735881928613879776080915431405451290973033569319514193671669728141214871416017947828875927229222881168169257475334995978506638522562727082841621103377534674314230094515648566698775749021699250522226914566251601033319352322004841943102716282077117990514212749731767331369952932713217468397590156019717599467826551), (151714288904469334580506311699687786932470047567590570627562909313285345196856604545832204480874695065076751985948503804773320989285516729101449384425625868713665574733542588482486855117947345613674296154473648201573294656067965326647224949611860214628357359309132040214209027790777151678914123082601456378886356732067541268132080748126762522835420758316631537412494961049197204205425016010352396151454741704273031546867105807470915616417638914866181520925045778461950631479727411682307627799765986827626393424093734894, 113195138575713276051356285353595608257964537355789624720904791904726154999652921625323202826448756838634725794845270773644628040704179463307506514170317679747518970223913451987204840944885539492431928207306649322098820553336366010453320453438302826748962194453073126072743462627626115533593121954332373216153303456196916042716877032156444624816270538578390571230115119658190341882710839242167009432905590403357945527537819618201757354986156989592243059863622832218854572529390202728216950457641950272095047333787845133), (143273408433100301029438629162157732007505901763968878422325872934638796541841921963880559171658699771599739944152860051396803691318827873678982069208535949317553094600976400547016789455183839578913564138947854902083200750061811236297222300037227275227735722169533644406492707041807445447669789156423983937337719273019297023253445936781670574157403858317609232724531493177053685096399564928522819896437359216101466084634086335795457115176098126076627222756666882660350843183492723945161110628940344165059531642659523383, 146674949633658124025273827347861739617972591213255422589451591241575751755759465692501605421798064451279436966144748850444994638018170033409916882690257065465451494369820928610739864416954101393861243749516295000434508472045269683452155382300622934680549683807475343006424675084022636524729510032850421728560842788745437895154746501644714259838329525121421521371090662294754870193345645037618193357860641995113251403596073075572702204621066922420230140482691977493775315013737307525071003333168203735454796604053833545), (249403491506281311380969267380571404400571727185603034767598580858666786446738167171913111309031464069379363518911333160553855193326393702713315185030611815951152637452746142527720323983558876002146517342279115230804997355865418057903304497673749142638365374144470739441077179470538767458050046177835858994825609702629664894934918018990719979984975720592480571603874761730644357479552994821055677150758155915862526298576933222903943787581240032930566464815465204077024966262935795336546362399011433775662246247111398239, 220026583481159087233455062019670620573362768860109890275771463721572578698600501321802550891913369288645565111669790293890107298985819301987334470845204887838326523986148919044265423495050278621214141338819744106934635120845496939830822733488219002062348108603935860045393020164701405072467539274006065291082813376084700667518290775010951235883727637485506655896607963039368820379051422268084714127890377382608847667294781936288634493994597515091795456078934847649806729629586190284753683050015906539243957697001022023), (215079273711572876410986208369683751294908183118379806386470679715006826521170132721726567905439942811382303605708056664603360017394551900388730088190217419850878783175574888901650563370610979038087942241376746471780988908912202971215079064900140401113825730922891606699754858802818433393292483508699051884185015859425552120339604916848864621271989828730706632512180758062407093767038158443746033606152375556179657992769575646334869657982412168590556206097067487695947784501185834313278349861463587166621658897486961285, 165567166071807415210098884820764709496153202096646908950619075676969166055854408565385662974546628510018441833788996418834797201726509458995351065808801225062402256327061845600825747669765288510624735507443675920510399006294180586052938942717561974376882538088092265694134635957495100715662266267357612266079433484517807375368429704206604635121324513004453596132019914682211594230617872219093487683074011218155282605906006194375075803005611967842695926548707579195433499994415413239784543530160970447676692869869775676), (228640244303908717297167044778358038077902415175263705677701277564554270721639076536848778203545648125859327404830206543807475124805809333701155019527553638924049712539331364884394462007690016542789938920025584886621196279327226524440087499458342989252357755491410890483133060523953494059732343775334979996866384865935940617099927020557347955903470709779090391882774438879675954149657556507819136838955515558446346085651316020265457443778053298058612260871138738040683307567599833900424381965386410969307647307369384337, 50165978141277819866049506699428057948802298519848104269621195645506935211584635274953826734316042747547515285609143893926944616496665386006349117172998096582280910144517457297702276740861716885437586834114054074206762165813673080314532603338459131607867567911958178781739505569816626312228165860061197202805933649452157563939564094961259760708185312146707171518968545037144370645198264879962319609864920134620742014988290980148541839415818403783076111150948944201550612135282717822173823751686257249500946118268104684), (260772944033526649752040603039686583353866815340829345188533891968004157467437167053710372219786485894088629376882326037936018907830890211870975702462740982328255444349717705245571849629146899762401559087996404759952457290427825581600106649293512652464779359266335650503918992764721684994867827583945612335934204038413816090349940775896656941750661067477541878792538967929065878101983413114812547001636708105307101185316535811926701056506444389655899925460725232919103379480543873872663434597493298813809089638160216500, 178822297670557205167893884671789644494733002710980842013844409963257117977727466427973839291798664502187859871290871392663447194614632215617775851356048586688401675157884835686198745209102861687009247775089840237122905831291304107610469327023876013149997285955560827672550035934501475882105008318345702835710511139568555607450691543879827538078967647488713788236537917448993732693958930584796688889209027167790147994500386404418863068804471331354407391195350272032834736051454815212017456171393538604058440084178785138), (153951520673385600585961203675637598772601638997436454635342055186847630642649668335965719208548586394720698759337915374432017680802144574982195131450687416186157048436598230083986127273557613203138054681250267787104668155803300164220352768363677389975389879906251331431662461990044058915429571767891876553813802059111070091377174616114219840922496478719633748862558761260936593076772050749815146554186743403077990697502097617642694431073886078861243520255713835477305063044518118066338897871379418786916048308001969642, 156677641648933384765684691841278862645672754960550364491841534426373366855026169555313043450342179770319758154010346709165462884527668929783331518815234286818109634304084831326103818198387741069702702752332554903172870825713486344211463198732464292089738363752466400950781915098607771340376959222392923586445885108829631888240542595711945606244159113099631894036295416012830825883435869636226984125330515770450372976608451137637329197460905623926500239295398492662897852793832046161329679123965719170637821852017541626), (182121275786448274703764860722207288688504251090526347386757201912164299971660589134892392593241000207363015377123532378065868724162125833912530972394915958665480631907067587572014039907112757035041814867937944633329495525743116952775108181544154895419181248880103117645953572669852637658173135330666489107513016628573955811775466684165143992392582744844394450653190459150090420140982302633882320923586679381748714431459394022990660732442705410510333910511438790458145935472292717646314404943912425265028499888510174598, 203440028868962984833821327933789556292629799184980205949050297313869882325162938301832971394230086020203937893809586214315999984427107160219912194805861777145741298008459998847103235243151628211509976280466653813611751247864428514134005135222162797493409369979305348203986570673847042670733283319660635425580706085693423174093318482780132615052711623695122664139057281605247745929023719568948004049990752313628422178360038895083650988297135247676372740583180753811984847210662578351383128821641159416840888477928682078), (218823575478368993955048790301926838437881143334348547262286809656812028268317304117409196876147138768171269470142474896692100140880755219823221990741488174315700621873115881799875553774369475082536987154562339321080637214185501516400621440388225723796980982899499623333730581949456459563202708568004908699142703905181478123703124547955265445070084332319889770567425486299504192535917180867591651719599910708571157067795615339103935726452179859088482325394789423729638822803813023195364259090039516707595275620606223098, 238360831921645517033282852001853402704192593646552818549162257086131847495832206207536403824297663424275603654870000653597808272307859106152007825595353459253005711098749795572570443393454435526757269349583998699531628152424144085951574812986232887851420719883402359586733609130991895552759814577684367961852962954957142339493218345367856462618197020620224169353973697144908034084747802499066704624535556265014878529090655506836355781206186508004035222663675445692924362410085183466479682020421951634577195038189582468), (7605308948924713893554832066864121414252483808305011091620612954856641658669367332357087398584404497275705301412227300132578417133173046053080772734818034453592192660914525809258158102936364260896213514380057335541283089086072298851758871406982865424218623716834685065557610594958011992745774101791101476219252968301741083316175066203079039213553580734030289747773949653701560564634653634860835561109658488968900667869196390219359276163732091789449610499277368225539853863255513232114666428859799256253673733736659934, 84338265593158215073600285774268951532171030715482815121324903198740799001477695481022777242719096465783467452535757377773297443527190828821051666329343779990168147101359925275718790254346877292701611345915823716088047741419538003476861653674067582773629818569266305858464954225803492630796727802186048224313050739888896540519497030255394106498300870595202213057412239405023629489623432730026664229571431460166590904128615265134596663917268529201962732873572258496676098364394367451264108741454944171782819942195095341), (260574236488407935488628660869550896326797079442686943514628661629687399953873851351524123117678854245330138146883940465164632401241414354283763993006051409910547635993821167683763784377300171479035704071118316710560399835534541136502396716751872135374863702011670440373059039486855344367530019761146394096881285791796980662052288525887698305777038723190087660859458441551938560031917347933816170298126009833562473518886720754679296740435464958844554206717306339055626973734868160598112213246395854439553619910006602141, 215031607965289395841597958782668037673484825089737077680116503967686961841667136969161392233440749102334833530419916926904430230760368898665628347399517114710948182534421920881834061302840221573802306449366480749919988514946580495147534756949978412713550979077019198599738941387116501782579306035864628214179812916834096486956736908275485194857938819787685023366084861770486853029181761022412161076373564613780204140998658159981842030287716923797731294561007312770312377377200056945449000311171752181205441965528935874), (198650576114165882449288026892214156276310958538011770523786728908105721360166101586279901877256531212257550264666494397314854415530372455940040150000010464517188336179827548221813135688964063397759290819652552869032850475218576198380858804434982221752101529325232884185525464193387767853411736259300751746214902051788858890055001236520152969180010172699764643110516920458462497046758742780733065725918173268086172671600452269919046762751217264939972190320714063861500100730343214043940778545664923273954431822712458287, 98575677753024287556019342929363679053982268955883779060795868148514132469159057938577626286714738458880375542997435176228749972239849021765147899018326553134629305587630983987645333121909724303395753140044547644366980019247720029923521164816180269979075442608444144431202613744990379185147853120702658487250116464883053687214761782785364318531008585387852132690487409708623886477690527271931747982661236178782523900957816260304362680211164984895592121752024391716149630257731393458732924761811426589241282290399095942), (133239237361361811696048540847458002212650695618301830827793891053639158166896674746134234523487135397403954524183567898886271486999571641531735158385404357658102658615539986689461289623145800299293935203492505727751870154133777899999222627625429326191129944696381042246624406490311860471634501715534659706946193422960549385790867868364451316422996956308516881589568763130787648575177095185336254852857468636860618577916534359157560688439784211466848879111128248465929528606516810076772919357973993801977193176114082633, 91993476954022760012798281670772708974247590300533609094245183822546756179517685689556735104286180548746323121584555720933324078992320978166897622353779701361126291322413292697697396543199293764590408581810818990685090527780478292097542106699940483205806149443174482967568300230425843760446653203856070462189339134604330157898491668720364014222964691584546427448260833308773860654718614894674905336051468516174232055942686622203957221449760803027397791234923638079424420066167267329350115771383830077528497272156638506), (95582621179135234162644663973759115030280708105173042864643748820898368161340863849390296104736276377098268450466214656481306123639700508027953901051290602167543644403815267941649482259183013123386204623097548703992945451692699742180719629475227930324881627331813906906508914901060228391057700936398107111821208803611542219630887301456153687209236199542403045434348094180112509184244726118896660624616403473132543257734828812611125323216911743462747983375152094663325459065388691057143880240380997574071376853464247035, 232352441732141135103454694828789409695750521085516707673246640367598676004047358260302254213092756665608390600758286850148614086134444187559526307489875627257575726111105762131815461870322981755137649000376767125396510619885683103239625485770683659802497093679638121418808084113118832714735551581184248380109440381623813485630097624684044974323307573190413869646763288463464923237420994040221148913548050627902538591565441845343995830686332202964403908307760184053940232271993381347882801989168889743238527356213855452), (258077403654756237716504509389411450264086564167441197441992247041683977605292742137327564976821856572413513401676985367106470072675968010369293214122880029016779939107521858890678568060848094862941480840987133595171797018800289787199783252896262873627767237196210053178254269524723135216496799679281365275621756340432147482265982099094739471498473746177912190376569719635941552555622213874734197454882799555744886325184069583870028520520148657134565959771591400315189969688904284018357614841113544340835425223265680147, 132619711305230755023718414178727374860129372168380541236154544169652117680402142337603417839580343610412910242758120828063112527040245594832613214330126362748191108746206127128051213878124100598393743003465997856657505974679274302377336989381816351610608074708062960998916948448170373532794915312522943031887089971768553107015227988908849150040972068906638987306481505099609598863656873588776064450399947837586887592565715213866014274642313127496432902232963787467375168488326815943797992382485889955510144119668259991)]
enc_flag =  5d130cc326373ca55bc593d06dfe84e33f52b5ef0d1eab5154d47c77c502663bd0a05196f5ad666c69d70ac94dcbb58ada1da640c8df212fd85968ace999e7c70ab1cb8a2050bbe4f82a570936e8b2fd5bf25d376d9cdfeaae1f94b842918ea1

This is the second part of the challenge, which uses ECC to encrypt the flag.

First, we see that it generates two prime numbers and , then random coordinates for a generator point of a curve on . The parameter of the curve is generated randomly, but the parameter is determined by , and (this is usually done to start with a point that belongs to the curve).

Then, they show us a value master_eye () which corresponds to the result of multiplying the order of the curve under and under . And also, they show us that , The point at infinity (in the curve under ). In some way, this value is like the order of , since by multiplying it times we obtain the identity element of the group.

Then, the server takes in the curve under and multiplies this point by 32 random values. Subsequently, it takes the sum of these random values to derive an AES key to encrypt the flag. They give us the result of multiplying all random values times , but not the random values and not even .

Curve parameters

We are in a fairly limited situation, since we have almost no information about the curve. However, we have 32 points (coordinates and ) and we know they belong to the curve.

Therefore, we know this:

If we use two of the points we have, we can get rid of the parameter :

If we do this with two other points, we have a similar equation:

And now we can multiply the first times and the second times to be able to eliminate :

Perfect, now we have an equation that is fulfilled and that only depends on the coordinates of 4 points and . We can use another 4 points to have similar equations:

If we pass all the terms aside, we have two values that are divisible by :

So, we can use the greatest common divisor (GCD) to recover (well, aactually a multiple of , but we can take away the small factors that we have).

Once we have the modulo on which it operates in the curve, it is already easier to find parameters and from any two points of the curve. We start from a previous expression:

Since we already know , we can calculate multiplicative inverses, and therefore, isolate :

And after finding , we can calculate as follows:

All this can be implemented with the following SageMath code:

x, y = [], []
for xx, yy in outputs[:8]:
    x.append(xx)
    y.append(yy)

kN2 = gcd((x[0] - x[1]) * (x[2] ** 3 - x[3] ** 3 - y[2] ** 2 + y[3] ** 2) - (x[2] - x[3]) * (x[0] ** 3 - x[1] ** 3 - y[0] ** 2 + y[1] ** 2), (x[4] - x[5]) * (x[6] ** 3 - x[7] ** 3 - y[6] ** 2 + y[7] ** 2) - (x[6] - x[7]) * (x[4] ** 3 - x[5] ** 3 - y[4] ** 2 + y[5] ** 2))
N2 = kN2

for pp in primes(1000):
    if N2 % pp == 0:
        N2 //= pp

N = isqrt(N2)

print(f'N^2 =', N2)
print(f'N =', N)

a = (y[0] ** 2 - y[1] ** 2 - x[0] ** 3 + x[1] ** 3) * pow(x[0] - x[1], -1, N2) % N2
b = (y[0] ** 2 - x[0] ** 3 - a * x[0]) % N2

print(f'{a = }')
print(f'{b = }')

And with this, we get the curve parameters:

$ sage solve_ecc.sage
N^2 = 264565577158994236590031855153889858642149293847448847970649031816068290144718943726237580763969647903770543375415221480423145106277967483944055518720771189157189592025839010707415649298934802554818600881343671391830933519779439364174223387859553464007199819265502917701981157545728448143450273367259289276152361264709006325795000613690279714089006075705019812688622337567736625576157696248463678172321658741121121141186095188499520441835623507334604791145463181077781478470093570533678182144421450743423516076239451209
N = 16265471931640785828934127858946752538285468297743536678369884769134613070708011877740082736319382017849667570641090507172991939418666182470818730451631260930161158328837538561881241462033418605418414010577396121712695567318179840613434951995896817726886735203
a = 255016168931197818685062305277467475939147310316032851940562629263766273806848827361574161304193387338790695002038199730358872156231618756413472252089556793554595535751713490844781606041715667333542594625070573351900213140641050218811210932150487739254199296509019565794946174873502371514562154033669982225110484375322837401197720028302647760803541964996213018205876600519059980832702437327295820859281072782162433368802258604600450884470883303464689592355860840174477238043947992440101763465668785090298241602420559775
b = 50127732115018484203170702229784545965146420529082726037385256846562169633784145549965749115939355046938153878636690046505434313448672070728706649287121339198111456597206969317341833429883720351526802757158855937829665701077162207162706822082172196818620358232889005030349353850169533514493407744045253838278286262204977117355796158321792643972401350420922296278450361220874255243965850220373605475047095584092551599895968561340721051061489824446629675800132597230488528303354169479640856219344579732617565600333600980

Generator point

From the generator point we know that its coordinates and are 257-bit integers, And we know that it satisfies the curve equation. In addition, as the curve modulo is , which has bits, we can define the following polynomial:

We get a root at , which is also small compared to the bits that has. Therefore, we can use the Coppersmith method on a bivariate polynomial to find this small root. To do this, we can use defund’s implementation, which admits multivariate polynomials:

load('coppersmith.sage')
P.<Gx, Gy> = PolynomialRing(Zmod(N2))
f = Gx ** 3 + a * Gx + b - Gy ** 2
roots = small_roots(f, (2 ** 257, 2 ** 257))
Gx, Gy = roots[0]
print(f'{Gx = }')
print(f'{Gy = }')

And here we have :

$ sage solve_ecc.sage
N^2 = 264565577158994236590031855153889858642149293847448847970649031816068290144718943726237580763969647903770543375415221480423145106277967483944055518720771189157189592025839010707415649298934802554818600881343671391830933519779439364174223387859553464007199819265502917701981157545728448143450273367259289276152361264709006325795000613690279714089006075705019812688622337567736625576157696248463678172321658741121121141186095188499520441835623507334604791145463181077781478470093570533678182144421450743423516076239451209
N = 16265471931640785828934127858946752538285468297743536678369884769134613070708011877740082736319382017849667570641090507172991939418666182470818730451631260930161158328837538561881241462033418605418414010577396121712695567318179840613434951995896817726886735203
a = 255016168931197818685062305277467475939147310316032851940562629263766273806848827361574161304193387338790695002038199730358872156231618756413472252089556793554595535751713490844781606041715667333542594625070573351900213140641050218811210932150487739254199296509019565794946174873502371514562154033669982225110484375322837401197720028302647760803541964996213018205876600519059980832702437327295820859281072782162433368802258604600450884470883303464689592355860840174477238043947992440101763465668785090298241602420559775
b = 50127732115018484203170702229784545965146420529082726037385256846562169633784145549965749115939355046938153878636690046505434313448672070728706649287121339198111456597206969317341833429883720351526802757158855937829665701077162207162706822082172196818620358232889005030349353850169533514493407744045253838278286262204977117355796158321792643972401350420922296278450361220874255243965850220373605475047095584092551599895968561340721051061489824446629675800132597230488528303354169479640856219344579732617565600333600980
Gx = 187542020032288314214490630204741820227829303492195652833504798640124300158900
Gy = 168843703689929435984972726423710110843417547332425176249556408870268071035700

Elliptic curve factorization method

Before being able to solve the discrete logarithm that will give us the key to decrypt the flag, we need to factor , because to solve the discrete logarithm in the curve under we need to solve it before in the curve under and under , and then use the Chinese Remainder Theorem (CRT) to bring together both results.

The factorization of is something peculiar, since it is necessary to understand how the Lenstra elliptic-curve factorization works:

  • If we want to factor a number , we define an elliptic curve under and a point on this curve (we can generate random coordinates and , a random parameter and then find a parameter to force the point to be in the curve)
  • The goal is to find a couple of points in which the sum of both is not well defined
  • To add two points, it is necessary to calculate the slope of the line that joins these points. If this line is vertical, the result is the point at infinity. If it turns out that the GCD of this slope value with is greater than , the point is not defined. But the important thing is that we will have a factor of

To apply this knowledge to the challenge, we have to remember the value of (master_eye) which holds that in the curve under :

sage: E = EllipticCurve(Zmod(N), [a, b])
sage: EM = EllipticCurve(Zmod(N2), [a, b])
sage:
sage: G = E((Gx, Gy))
sage: m = 1626547193164078582893412785894675253828546829774353667836988476965589408066956214779521399108300576899339435850978322322115885861611495653342922478
....: 0974963093860223870869151381622793452378040102391285088110131930993214655276327069828109098832154854719776594644
sage: m * G
(0 : 1 : 0)
sage:
sage: P = EM(outputs[0])
sage: m * P
...
ZeroDivisionError: Inverse of 16265471931640785828934127858946752538285468297743536678369884769134613070708011877740082736319382017849667570641090507172991939418666182470818730451631260930161158328837538561881241462033418605418414010577396121712695567318179840613434951995896817726886735203 does not exist (characteristic = 264565577158994236590031855153889858642149293847448847970649031816068290144718943726237580763969647903770543375415221480423145106277967483944055518720771189157189592025839010707415649298934802554818600881343671391830933519779439364174223387859553464007199819265502917701981157545728448143450273367259289276152361264709006325795000613690279714089006075705019812688622337567736625576157696248463678172321658741121121141186095188499520441835623507334604791145463181077781478470093570533678182144421450743423516076239451209 = 16265471931640785828934127858946752538285468297743536678369884769134613070708011877740082736319382017849667570641090507172991939418666182470818730451631260930161158328837538561881241462033418605418414010577396121712695567318179840613434951995896817726886735203*16265471931640785828934127858946752538285468297743536678369884769134613070708011877740082736319382017849667570641090507172991939418666182470818730451631260930161158328837538561881241462033418605418414010577396121712695567318179840613434951995896817726886735203)

We see that errors appear that the point is not defined. We still do not find a factor of , because the error says that there is no inverse of modulo .

What we can do is find some factors of using factordb.com:

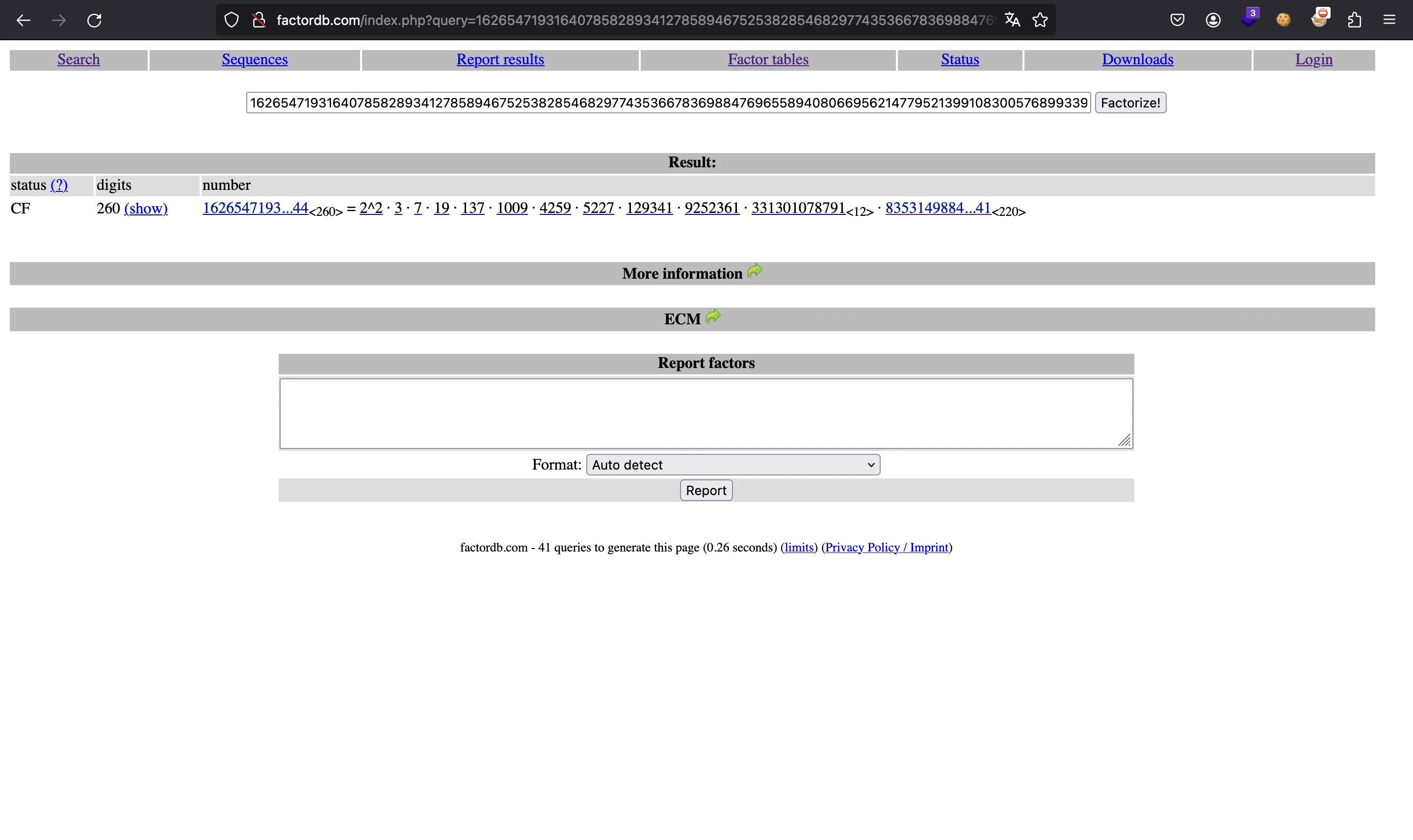
El Reset de 1745 5

And now, instead of multiplying for , we remove some factor. And after trying a bit, we see a somewhat different mistake:

sage: (m // (2 ** 2 * 3)) * P
...
ZeroDivisionError: Inverse of 3306666750998407949290614826810384435005357289027507523518097170844397310630405493724231782674473208511099023446178055658897571567 does not exist (characteristic = 264565577158994236590031855153889858642149293847448847970649031816068290144718943726237580763969647903770543375415221480423145106277967483944055518720771189157189592025839010707415649298934802554818600881343671391830933519779439364174223387859553464007199819265502917701981157545728448143450273367259289276152361264709006325795000613690279714089006075705019812688622337567736625576157696248463678172321658741121121141186095188499520441835623507334604791145463181077781478470093570533678182144421450743423516076239451209 = 3306666750998407949290614826810384435005357289027507523518097170844397310630405493724231782674473208511099023446178055658897571567*80009749116421201819460392082932543369781073296146200526104333277735370142669725871106604546514530470592721417838917956283421712140325370081541030574865070485541235289513992448161233817820635108170971961669125453845627344044069052189301381281546319302677223308512323449970971168044792073413850208786719548578234348518037138428508360825551264023856385886924097308601393744682119824794566727)

Here we have a factor of :

sage: p = 3306666750998407949290614826810384435005357289027507523518097170844397310630405493724231782674473208511099023446178055658897571567
sage: N % p
0
sage: q = N // p

Discrete logarithm

The last step that remains is to solve a discrete logarithm. The server calculates 32 random values and multiplies them times in the curve under :

Then it uses the sum to derive the AES key that encrypts the flag.

An option is to solve 32 discrete logarithms and then add all the results. However, it seems more efficient to add all points and solve a single discrete logarithm, resulting in , because:

Even so, it is not trivial to solve this discrete logarithm because we are in a curve under . A curve defined under a composite modulus can be broken down into the “product” of several curves defined under prime modules (more information in crypto.stackexchange.com). A challenge that can serve as an example is Ecchimera from CryptoCTF 2021.

And on the other hand, after investigating how to solve this discrete logarithm, we find a challenge called “pure division” from the zer0pts CTF 2021, and two writeups that show how to solve it:

In this challenge, a curve defined modulo . To solve it, it is necessary to redefine the curve under /-adic numbers) with digits of precision. In this field, discrete logarithm is easy to solve because there is an isomorphism between the points of the curve and .

Although the background of the attack is highly complex, the implementation in SageMath is quite simple. For our case, we have to put the points of the curve in and , solve the discrete logarithms and then use the CRT to obtain the result in the curve defined under :

sage: EM = EllipticCurve(Zmod(N2), [a, b])
sage: G = EM((Gx, Gy))
sage: P = sum(map(EM, outputs))
sage:
sage: Ep_order = EllipticCurve(GF(p), [a, b]).order()
sage:
sage: EQp = EllipticCurve(Qp(p, 2), [a, b])
sage: pG = EQp(G[0] % (p ** 2), G[1] % (p ** 2)) * Ep_order
sage: pP = EQp(P[0] % (p ** 2), P[1] % (p ** 2)) * Ep_order
sage:
sage: sol_p = ZZ((pP[0] / pP[1]) / (pG[0] / pG[1]))
sage: sol_p * pG == pP
True
sage:
sage: Eq_order = EllipticCurve(GF(q), [a, b]).order()
sage:
sage: EQq = EllipticCurve(Qp(q, 2), [a, b])
sage: qG = EQq(G[0] % (q ** 2), G[1] % (q ** 2)) * Eq_order
sage: qP = EQq(P[0] % (q ** 2), P[1] % (q ** 2)) * Eq_order
sage:
sage: sol_q = ZZ((qP[0] / qP[1]) / (qG[0] / qG[1]))
sage: sol_q * qG == qP
True
sage:
sage: sol = crt([sol_p, sol_q], [p, q])
sage: sol * G == P
False

However, this solution is not correct since the last condition is not met. But the previous conditions are fulfilled.

What is happening here is that this solution is in modulo , and is the result of adding 32 numbers lower than . Therefore, it is expected that the sum is somewhat greater than , and the result we have is smaller:

sage: sol < N
True

So, we can add to the result until the condition is satisfied (less than 32 iterations):

sage: while sol * G != P:
....:     sol += N
....:
sage: sol // N
14
sage: sol
228783371310953134200979693682284782082294455467926861967477800951173709471659482447103308284512776967919781995204775749869580375084462240509528430246695076210060525582252947319050463647309271053406795093984733161889288695889919185344579992689803192397436707284

And that’s it. With this number we can derive the AES key.

Flag

Finally, we can decrypt the flag with AES:

$ python3 -q
>>> from hashlib import sha256
>>> from Crypto.Cipher import AES
>>> from Crypto.Util.Padding import unpad
>>>
>>> key = sha256(b'228783371310953134200979693682284782082294455467926861967477800951173709471659482447103308284512776967919781995204775749869580375084462240509528430246695076210060525582252947319050463647309271053406795093984733161889288695889919185344579992689803192397436707284').digest()
>>>
>>> unpad(AES.new(key, AES.MODE_CBC, b'iseeyou!' * 2).decrypt(ct), 32)
b'HackOn{3r3s_un4_l3y3nd4_d3_l4_cr1pt0_y_s1nc3r4m3nt3_b4st4nt3_r3pt1li4n0}'