Calibrator
6 minutes to read
We are given a remote instance to connect to:
$ nc 165.227.224.40 31139
[OK] Memory check
[OK] Syncing filesystem
[OK] Detecting sensors
[OK] Module loader
[OK] Reading configurations
Inititing calibration process ...
┌──────────────────────────────────────────────────────────────────────┐
│┼───────────────────┼────────────────────────┼┼──────────────────────┼│
││ XenoCal 2000 │ . ││ ││
│┼───────────────────┤ ┌─┐ x││ . . ││
││ Iteration: 42 │ x ► └─┘ ││ x ││
│┼─────────┬─────────┤ ││ ││
││ X:1337 │ Y:65189 │ . x ┌───┼┼───┐ ││
│┼─────────┴─────────┘ x ┌─┘ ││ └─┐ x ││
││ . ┌─┘ ││ └─┐ ││
││ ┌─┐ x ▼ ┌┘ . ││ └┐ x ││
││ └─┘ . ┌┘ ││ └┐ ││
││ . │ ││ . │ ││
│┼──────────────────────────────────┼─────────┼┼─────────┼────────────┼│
││ x │ x ││ │ ▼ ││
││ x ──►x └┐ ││ ┌┘ ││
││ . ▼ └┐ ││ ┌┘ . ││
││ . └─┐ ││ ┌─┘ ││
││ ┌─┐ x └─┐ ││ ┌─┘ x ││
││ └─┘ ┌─┐ ┌─┐ └───┼┼───┘ ││
││ └─┘ └─┘ ││ ││
││ x . . ││ . ││
││ . x ││ x ││
││ x ▼ x . ││ x ││
││ ││ ││
│┼────────────────────────────────────────────┼┼──────────────────────┼│
└──────────────────────────────────────────────────────────────────────┘ ┌─
│
┌─┬───────────────────────────┬─┐ ┌──────┐ ┌───┼┐
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ │[=()=]│ ├────┤
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ ┌──┼──────┼──┐ │ │
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ │◄├┼┼┼┼┼┼┼┼┤►│ │ │
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ └──┼──────┼──┘ ├────┤
└─┴───────────────────────────┴─┘ │[=()=]│ └────┘
└──────┘
Iteration 0:
>
Source code analysis
And we also have the source code in Python:
from FLAG import flag
import random
import math
import time
ITERATIONS = 47
SIDE_LENGTH = 2 * 10 ** 9
ATTEMPTS = 300
HI = SIDE_LENGTH // 2
LO = -SIDE_LENGTH // 2
def banner():
banner = """
┌──────────────────────────────────────────────────────────────────────┐
│┼───────────────────┼────────────────────────┼┼──────────────────────┼│
││ XenoCal 2000 │ . ││ ││
│┼───────────────────┤ ┌─┐ x││ . . ││
││ Iteration: 42 │ x ► └─┘ ││ x ││
│┼─────────┬─────────┤ ││ ││
││ X:1337 │ Y:65189 │ . x ┌───┼┼───┐ ││
│┼─────────┴─────────┘ x ┌─┘ ││ └─┐ x ││
││ . ┌─┘ ││ └─┐ ││
││ ┌─┐ x ▼ ┌┘ . ││ └┐ x ││
││ └─┘ . ┌┘ ││ └┐ ││
││ . │ ││ . │ ││
│┼──────────────────────────────────┼─────────┼┼─────────┼────────────┼│
││ x │ x ││ │ ▼ ││
││ x ──►x └┐ ││ ┌┘ ││
││ . ▼ └┐ ││ ┌┘ . ││
││ . └─┐ ││ ┌─┘ ││
││ ┌─┐ x └─┐ ││ ┌─┘ x ││
││ └─┘ ┌─┐ ┌─┐ └───┼┼───┘ ││
││ └─┘ └─┘ ││ ││
││ x . . ││ . ││
││ . x ││ x ││
││ x ▼ x . ││ x ││
││ ││ ││
│┼────────────────────────────────────────────┼┼──────────────────────┼│
└──────────────────────────────────────────────────────────────────────┘ ┌─
│
┌─┬───────────────────────────┬─┐ ┌──────┐ ┌───┼┐
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ │[=()=]│ ├────┤
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ ┌──┼──────┼──┐ │ │
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ │◄├┼┼┼┼┼┼┼┼┤►│ │ │
│ │┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼┼│ │ └──┼──────┼──┘ ├────┤
└─┴───────────────────────────┴─┘ │[=()=]│ └────┘
└──────┘
"""
print(banner)
def load():
boot_messages = \
"""
[\033[92mOK\033[0m] Memory check
[\033[92mOK\033[0m] Syncing filesystem
[\033[92mOK\033[0m] Detecting sensors
[\033[92mOK\033[0m] Module loader
[\033[92mOK\033[0m] Reading configurations
Inititing calibration process ...
""".split('\n')
for m in boot_messages:
print(m)
time.sleep(random.random())
# Calibrator's error acceptance threshold
e = 2
if __name__ == '__main__':
load()
banner()
for i in range(ITERATIONS):
print(f"Iteration {i}:")
R = random.randint(SIDE_LENGTH // 4, SIDE_LENGTH // 2)
X = random.randint(LO + R, HI - R)
Y = random.randint(LO + R, HI - R)
for a in range(ATTEMPTS):
line = input("> ")
x, y = [int(n) for n in line.split(' ')]
D = math.sqrt((X - x) ** 2 + (Y - y) ** 2)
if D <= e:
print("\033[94mREFERENCE", end="\n\033[0m")
break
elif D <= R:
print("\033[92mDETECTED", end="\n\033[0m")
else:
print("\033[91mUNDETECTED", end="\n\033[0m")
else:
exit(0)
print(flag)
The challenge runs 47 iterations, and in each iteration, we are given 300 attempts to input a point for-else syntax existed in Python. The else blocks executes when the for loop is finished (more information at www.w3schools.com), but not if a break statement exits the loop.
So, looking again at the challenge code, we need to enter the if statement where D <= e, so that break is called and the server does not call exit(0).
Drawing the problem
On each iteration, we must enter a point LO, HI and SIDE_LENGTH).
In order to pass the iteration, we must enter a point DETECTED. And if UNDETECTED.
The following figure shows all these sections:
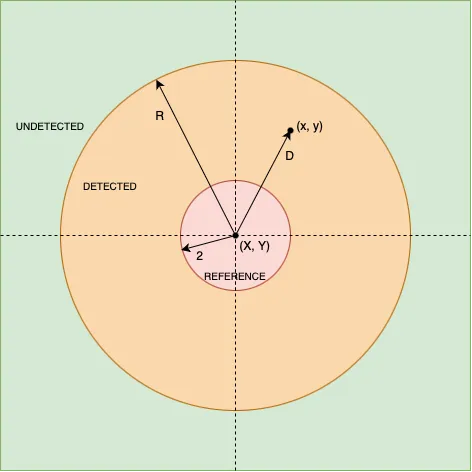
Notice that we don’t know any of DETECTED, UNDETECTED to somehow find a point REFERENCE.
Binary search
Since we have only 300 attempts, we must find a quick searching algorithm that allows us to find a REFERENCE point. Since we have a “binary” oracle (DETECTED or UNDETECTED), we will try to find a way to apply binary search.
The objective is to find 0 to HI), so that
Then, we will do another binary search on point LO to 0), so that
Analogously, the other two binary search algorithms will output
Therefore, we can construct this system of equations:
Subtracting the first two equations and the last two, we have this reduced system of equations:
So, we can isolate
Once we know the point
Flag
After programming the above procedure, we execute the script and eventually find the flag:
$ python3 solve.py 165.227.224.40:31139
[+] Opening connection to 165.227.224.40 on port 31139: Done
[+] Round: Done
[+] HTB{b1n4ry_s34rch_15_und3rr4t3d}
[*] Closed connection to 165.227.224.40 port 31139
The full script can be found in here: solve.py.