Tsayaki
6 minutes to read
We are given the source code of the server in Python:
from tea import Cipher as TEA
from secret import IV, FLAG
import os
ROUNDS = 10
def show_menu():
print("""
============================================================================================
|| I made this decryption oracle in which I let users choose their own decryption keys. ||
|| I think that it's secure as the tea cipher doesn't produce collisions (?) ... Right? ||
|| If you manage to prove me wrong 10 times, you get a special gift. ||
============================================================================================
""")
def run():
show_menu()
server_message = os.urandom(20)
print(f'Here is my special message: {server_message.hex()}')
used_keys = []
ciphertexts = []
for i in range(ROUNDS):
print(f'Round {i+1}/10')
try:
ct = bytes.fromhex(input('Enter your target ciphertext (in hex) : '))
assert ct not in ciphertexts
for j in range(4):
key = bytes.fromhex(input(f'[{i+1}/{j+1}] Enter your encryption key (in hex) : '))
assert len(key) == 16 and key not in used_keys
used_keys.append(key)
cipher = TEA(key, IV)
enc = cipher.encrypt(server_message)
if enc != ct:
print(f'Hmm ... close enough, but {enc.hex()} does not look like {ct.hex()} at all! Bye...')
exit()
except:
print('Nope.')
exit()
ciphertexts.append(ct)
print(f'Wait, really? {FLAG}')
if __name__ == '__main__':
run()
This challenge is kind of the second part of Iced TEA, because the server also uses Tiny Encryption Algorithm (TEA).
Source code analysis
What the server wants us to do is to take a given plaintext message, then provide a ciphertext and for different keys so that encrypting the plaintext with each of the keys results in the provided ciphertext:
Equivalent keys
After searching a bit, we find out that TEA has a total of 4 equivalent keys (more information at crypto.stackexchange.com). You can find a more formal explanation at Section 2.5 of this paper.
The key is in the key schedule algorithm (taken from Iced TEA):
def encrypt_block(self, msg):
m0 = b2l(msg[:4])
m1 = b2l(msg[4:])
K = self.KEY
msk = (1 << (self.BLOCK_SIZE//2)) - 1
s = 0
for i in range(32):
s += self.DELTA
m0 += ((m1 << 4) + K[0]) ^ (m1 + s) ^ ((m1 >> 5) + K[1])
m0 &= msk
m1 += ((m0 << 4) + K[2]) ^ (m0 + s) ^ ((m0 >> 5) + K[3])
m1 &= msk
m = ((m0 << (self.BLOCK_SIZE//2)) + m1) & ((1 << self.BLOCK_SIZE) - 1) # m = m0 || m1
return l2b(m)
In TEA, the key is formed by 16-bytes, which is splitted into 4 keys of 4 bytes each (K[0], K[1], K[2] and K[3]).
In each of the 32 rounds of the above for loop, there are XOR operations that involve K[0] and K[1] in one sentence, and then K[2] and K[3] in another sentence.
Due to XOR properties and the numbers that are involved, we can complement the most significant bits of K[0] and K[1] and achieve the same result, because K[2] and K[3].
We can test it as follows (using the solution from Iced TEA):
$ python3 -q
>>> from os import urandom
>>> from tea import Cipher as TEA
>>>
>>> pt = urandom(16)
>>>
>>> key1 = int('0' + '0' * 31 + '0' + '0' * 31 + '0' + '0' * 31 + '0' + '0' * 31, 2).to_bytes(16, 'big')
>>> key2 = int('0' + '0' * 31 + '0' + '0' * 31 + '1' + '0' * 31 + '1' + '0' * 31, 2).to_bytes(16, 'big')
>>> key3 = int('1' + '0' * 31 + '1' + '0' * 31 + '0' + '0' * 31 + '0' + '0' * 31, 2).to_bytes(16, 'big')
>>> key4 = int('1' + '0' * 31 + '1' + '0' * 31 + '1' + '0' * 31 + '1' + '0' * 31, 2).to_bytes(16, 'big')
>>>
>>> TEA(key1).encrypt(pt) == TEA(key2).encrypt(pt) == TEA(key3).encrypt(pt) == TEA(key4).encrypt(pt)
True
So, instead of using a padding of 31 bits set to zero, we can use random bits, so that no key is repeated.
Implementation
In Python, we can use the following code:
io = get_process()
rounds = io.progress('Round')
io.recvuntil(b'Here is my special message: ')
server_message = bytes.fromhex(io.recvline().decode())
for r in range(10):
rounds.status(f'{r + 1} / 10')
randoms = [''.join(choices('01', k=31)), ''.join(choices('01', k=31)), ''.join(choices('01', k=31)), ''.join(choices('01', k=31))]
key = int('0' + '0'.join(randoms), 2).to_bytes(16, 'big')
ct = TEA(key, IV).encrypt(server_message)
io.sendlineafter(b'Enter your target ciphertext (in hex) : ', ct.hex().encode())
for a, b, c, d in [[0, 0, 0, 0], [0, 0, 1, 1], [1, 1, 0, 0], [1, 1, 1, 1]]:
key = int(str(a) + randoms[0] + str(b) + randoms[1] + str(c) + randoms[2] + str(d) + randoms[3], 2).to_bytes(16, 'big')
io.sendlineafter(b'Enter your encryption key (in hex) : ', key.hex().encode())
rounds.success('10 / 10')
io.success(io.recvline().decode())
However, we are still missing the IV. The server uses TEA in CBC mode, but the IV is fixed (imported from a secret module).
This is easy to solve, because when we connect to the server and send a wrong ciphertext, the server will show what was the correct ciphertext:
print(f'Hmm ... close enough, but {enc.hex()} does not look like {ct.hex()} at all! Bye...')
Since we provide the key, we simply encrypt the given plaintext with a zero IV and then try to decrypt the ciphertext using CBC mode:
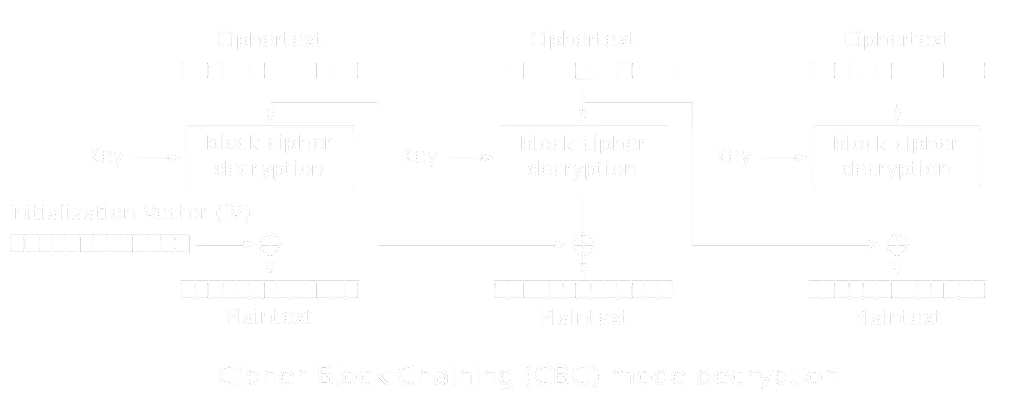
Since the server encrypts with a fixed IV, the first block of plaintext will be different from the one given initially by the server (because the zero IV is wrong). To get the correct IV, we only need to XOR the decrypted plaintext block and the given plaintext block:
io = get_process()
io.recvuntil(b'Here is my special message: ')
server_message = bytes.fromhex(io.recvline().decode())
key = b'asdf' * 4
IV = b'\0' * 8
io.sendlineafter(b'Enter your target ciphertext (in hex) : ', b'00' * 20)
io.sendlineafter(b'Enter your encryption key (in hex) : ', key.hex().encode())
io.recvuntil(b'Hmm ... close enough, but ')
ct = bytes.fromhex(io.recvuntil(b' ', drop=True).decode())
IV = xor(server_message[:8], TEA(key, IV).decrypt(ct)[:8])
io.close()
Flag
So, if we run the script, we will get the flag:
$ python3 solve.py 83.136.254.16:56803
[+] Opening connection to 83.136.254.16 on port 56803: Done
[*] Closed connection to 83.136.254.16 port 56803
[+] Opening connection to 83.136.254.16 on port 56803: Done
[+] Round: 10 / 10
[+] Wait, really? HTB{th1s_4tt4ck_m4k3s_T34_1n4ppr0pr14t3_f0r_h4sh1ng!}
[*] Closed connection to 83.136.254.16 port 56803
The full script can be found in here: solve.py.