<- HTB UNICTF

Clutch

22 minutes to read

We are given the following Python code that implements a quantum algorithm for key distribution:

from hashlib import sha256
from random import uniform
import json

from Crypto.Util.Padding import unpad
from Crypto.Cipher import AES

from secret import SECRET_MESSAGE
from alice import Alice
from bob import Bob

def json_print(message):
    print(json.dumps(message))

# Python implementation of the Frame-based QKD protocol described here : https://www.mdpi.com/2073-8994/12/6/1053
class QKD:
    # ...


def main():
    json_print({"info": "To all ships of The Frontier Board, use your secret key to get the coordinates of The Starry Spurr"})
    
    json_print({"info": "Initializing QKD..."})

    while True:
        qkd = QKD(Alice, Bob)
        public = qkd.execute()
        
        json_print(public)

        if "error" not in public:
            status = qkd.check_status()
            json_print(status)
            break

    json_print({"info": "Initialization completed. Only trusted ships can send valid commands"})

    while True:
        try:
            data = json.loads(input("> "))
            encrypted_command = bytes.fromhex(data["command"])
            assert len(encrypted_command) % 16 == 0
        except:
            json_print({"error": "Invalid input. Please, try again"})
            continue

        command = qkd.decrypt_command(encrypted_command)
        
        if command == "OPEN THE GATE":
            FLAG = open('flag.txt').read()
            json_print({"info": f" Welcome to The Frontier Board, the coordinates of The Starry Spurr are {SECRET_MESSAGE}{FLAG}"})  
            exit()

        else:
            json_print({"error": "Unknown command. Please, try again"})


if __name__ == '__main__':
    main()

The project is made out of four files:

  • server.py
  • alice.py
  • bob.py
  • helpers.py

There is a link to a paper that presents the quantum algorithm that is implemented in Python. We will be analyzing the algorithm and the code.

The algorithm is called Frame-based Quantum Key Distribution (QKD), and it allows two parties (Alice and Bob) to share a secret in a secure way over an insecure channel while using quantum computing. In this challenge we are in the position of Eve, a malicious user that can eavesdrop the communication between Alice and Bob, and we will need to find the shared secret among them, which should be hard to find from Eve’s position.

Therefore, we might think that the QKD algorithm is correct and the Python implementation has a bug that allows us to extract sensitive information. But it is also possible that the QKD algorithm is not completely good, although it is published in a research journal, and we need to find a flaw to get the shared secret.

Background

This challenge needs some knowledge about quantum computing. I’m not probably prepared to write rigorous quantum stuff here yet, but I will try to express some key concepts:

  • In quantum computing, qbits don’t have a certain value, they have a superposition state. It means that they can have any value, until the qbit is measured. Once a qbit is observed, it collapses to a value (0 or 1) and it cannot be changed. And this happens with some probability, that can be expressed as $\ket{\psi} = \alpha \cdot \ket{0} + \beta \cdot \ket{1}$, where $|\alpha|^2$ and $|\beta|^2$ represent the probability of collapsing to 0 or 1, thus $|\alpha|^2 + |\beta|^2 = 1$

  • A Hadamard gate (H) produces a “change of basis”:

    • $H \ket{0} = \displaystyle\frac{1}{\sqrt{2}} \big(\ket{0} + \ket{1}\big) \equiv \ket{+}$

    • $H \ket{1} = \displaystyle\frac{1}{\sqrt{2}} \big(\ket{0} - \ket{1}\big) \equiv \ket{-}$

  • Measuring a qbit that has been transformed by a Hadamard gate has 50% chance of collapsing to 0 or 1

The paper uses the following notation: $\ket{0_\mathrm{Z}}$ and $\ket{1_\mathrm{Z}}$ for qbits polarized with the standard basis, and $\ket{0_\mathrm{X}}$ and $\ket{1_\mathrm{X}}$ for qbits polarized with the Hadamard basis (that is, apply a Hadamard gate before measuring).

This means that if one measures using $\mathrm{Z}$, then $\ket{0_\mathrm{Z}}$ collapes to 0 and $\ket{1_\mathrm{Z}}$ collapses so 1 with 100% probability, while measuring any of $\ket{0_\mathrm{X}}$ or $\ket{1_\mathrm{X}}$ will collapse either to 0 or 1 with exactly 50% probability. The same happens in reverse when measuring with $\mathrm{X}$.

The QKD algorithm is mainly based in the use of non-orthogonal qbits. The purpose is that Alice sends a pair of qbits that are non-orthogonal, chosen at random and polarized with $\mathrm{X}$ and $\mathrm{Z}$, in this order. Actually, there are only 4 possible non-orthogonal pairs:

  • $(\ket{0_\mathrm{X}}, \ket{0_\mathrm{Z}})$
  • $(\ket{0_\mathrm{X}}, \ket{1_\mathrm{Z}})$
  • $(\ket{1_\mathrm{X}}, \ket{0_\mathrm{Z}})$
  • $(\ket{1_\mathrm{X}}, \ket{1_\mathrm{Z}})$

Then, Bob measures with either $\mathrm{Z}$ or $\mathrm{X}$, so that one of the qbits is always measured correctly. The author uses the term double matching to refer the fact of measuring the same value on both qbits. For example, if Bob receives $(\ket{0_\mathrm{X}}, \ket{1_\mathrm{Z}})$ and measures with $\mathrm{X}$, he can decode as either $(0, 0)$ or $(0, 1)$. The former is a double matching, whereas the latter is not.

Another concept to learn before diving into the QKD protocol is a binary frame (or simply, frame). This is just a matrix of non-orthogonal qbit pairs. For instance, pairs $(\ket{1_\mathrm{X}}, \ket{1_\mathrm{Z}})$ and $(\ket{0_\mathrm{X}}, \ket{1_\mathrm{Z}})$ can be arranged like

$$ \begin{pmatrix} \ket{1_\mathrm{X}} & \ket{1_\mathrm{Z}} \\ \ket{0_\mathrm{X}} & \ket{1_\mathrm{Z}} \end{pmatrix} $$

The paper shows in Table 3 that not all frames are useful, there are only 6 that are useful for the QKD protocol, while some of the useless frames can be used as auxiliary frames for error detection and correction.

Finally, the concept of matching result is the configuration that results from Bob’s measurement when obtaining a double matching. For instance, if Bob measures $(\ket{1_\mathrm{X}}, \ket{1_\mathrm{Z}})$ with $\mathrm{Z}$ and gets $(1, 1)$, and then measures $(\ket{0_\mathrm{X}}, \ket{1_\mathrm{Z}})$ with $\mathrm{X}$ and gets $(0, 0)$, the matching result can be represented as

$$ \begin{pmatrix} - & \ket{\bullet_\mathrm{Z}} \\ \ket{\bullet_\mathrm{X}} & - \end{pmatrix} $$

Since Bob got a matching result while measuring the first pair with $\mathrm{X}$ and the second pair with $\mathrm{Z}$. Table 4 in the paper shows the 4 possible arrangements and encodes them like bits 00, 01, 10, 11 for later decoding.

Frame-based QKD

I’ll show the steps of the algorithm and then we will do a short example using the source code:

  1. Alice sends $n$ pairs chosen randomly from the set of 4 possible pairs
  2. Bob chooses the basis to measure each of the $n$ pairs, randomly between whether $\mathrm{X}$ or $\mathrm{Z}$
  3. Bob tells the indices of the pairs that got double matching
  4. Alice takes the indices and performs 2-combinations to form frames, and discards useless ones
  5. Alice sends the frames to Bob as tuples of indices
  6. Bob computes sifting strings (sifting bits and measured bits) and sends them to Alice
  7. Alice is capable of getting Bob’s matching results to learn his basis choices for each qbit pair
  8. Alice and Bob compute a shared secret based on Bob’s measurement basis

Figure 6 in the paper shows the following flow:

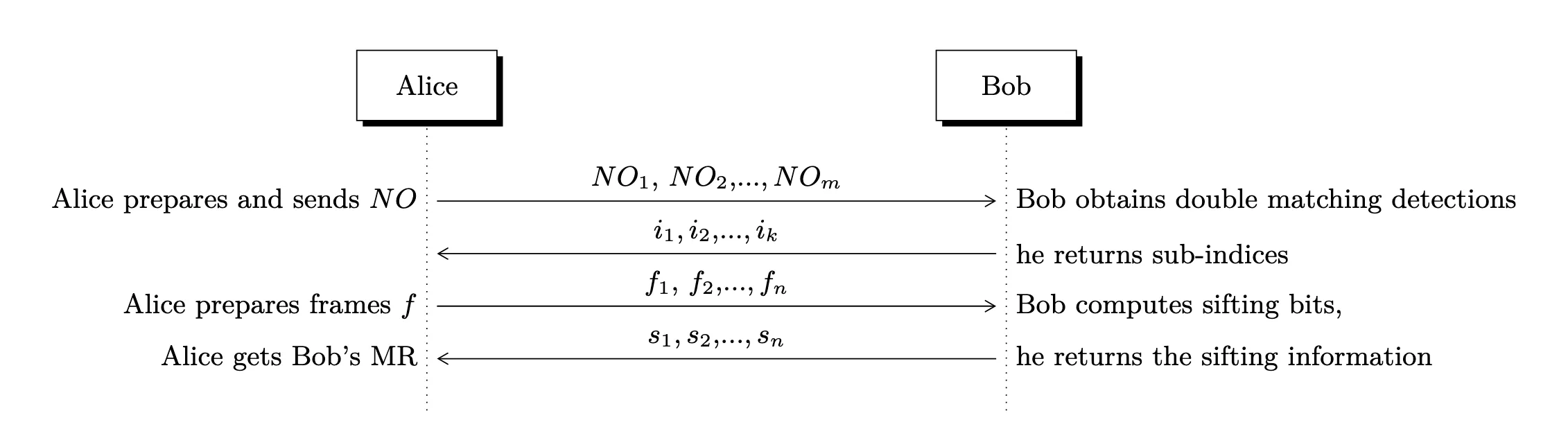
Clutch 5

There is an additional step before deriving the shared key. Alice must find ambiguous frames and tell Bob which frames are ambiguous, so that they don’t use those frames.

Source code analysis

The top-level protocol can be read in the QKD class from server.py:

class QKD:
    def __init__(self, Alice, Bob, pairs = 256, security = 256):
        self.Alice = Alice(pairs)
        self.Bob = Bob(uniform(0, 1))

        self.security = security

    def check_status(self):
        return {"status": "OK", "QBER": self.Bob.depolarizing_probability}

    def execute(self):
        pairs = self.Alice.prepare()
        double_matchings = self.Bob.measure(pairs)

        if not len(double_matchings):
            return {"error": "Key exchange failed, there's no double matchings. Retrying..."}
    
        frames, usable_frames, auxiliary_frames = self.Alice.compute_frames(double_matchings)

        if not len(frames):
            return {"error": "Key exchange failed, there's no frames. Retrying..."}

        bob_sifting_strings = self.Bob.compute_sifting_strings(frames)

        alice_sifting_strings, ambiguous_frames = self.Alice.error_correction(usable_frames, auxiliary_frames, bob_sifting_strings)

        alice_key = self.Alice.generate_shared_key(frames, usable_frames, ambiguous_frames, alice_sifting_strings, bob_sifting_strings)  

        bob_key = self.Bob.generate_shared_key(frames, ambiguous_frames, bob_sifting_strings)

        if len(alice_key) < self.security:
            return {"error": "Key exchange failed, the instance does not satisfy the security requirements. Retrying..."}

        if alice_key != bob_key:
            return {"error": "Key exchange failed, both keys are not equal. Retrying..."}

        bob_sifting_strings = list(bob_sifting_strings.values())

        public = {
            "double_matchings": double_matchings,
            "frames": frames,
            "sifting_strings": bob_sifting_strings,
            "ambiguous_frames": ambiguous_frames
        }

        self.shared_key = alice_key.encode()

        return public

Step 1: First of all, Alice generates random non-orthogonal qbit pairs (by default, a total of 256), and they are saved in pairs_data:

class Alice:
    def __init__(self, pairs):
        self.pairs = pairs
        self.pairs_data = {}
        
        # Setting up global parameters. Local variables with the same name refers to the frames generated in the actual QKD instance  
        self.usable_frames = USABLE_FRAMES
        self.usable_frames_iterable = list(self.usable_frames.keys())

        self.auxiliary_frames = AUXILIARY_FRAMES
        self.auxiliary_frames_iterable = list(self.auxiliary_frames.keys())
        
        self.generate_pairs()
        
    def generate_pairs(self):
        for i in range(self.pairs):
            x, z = [ randbits(1) for _ in range(2) ]
            self.pairs_data[i] = f"{x}x,{z}z"

    def prepare(self):
        pairs = []
        for i in range(self.pairs):
            circuits = self.generate_circuits(self.pairs_data[i])
            pairs.append(circuits)
        return pairs
            
    def generate_circuits(self, pair):
        x, z = [ int(state[0]) for state in pair.split(",") ]
        circuits = [ QuantumCircuit(1, 1) for _ in range(2) ]
        
        if x: circuits[0].x(0)
        if z: circuits[1].x(0)
        
        circuits[0].h(0)
        
        return circuits

The returning value of Alice.prepare is a list of quantum circuits that encode the qbit pairs. These circuits are very simple, they just use X and H gates to get one of the possible 4 non-orthogonal qbit pairs. So, nothing really interesting to see here.

Step 2: Then, Bob measures each circuit using a random basis:

class Bob:
    def __init__(self, depolarizing_probability = 0):
        self.depolarizing_probability = depolarizing_probability
        
        self.measurement_basis = {}
        self.measurement_results = {}
        self.backend = Aer.get_backend("qasm_simulator")

    def noise_model(self, p):
        error_model = depolarizing_error(p, 1)
        
        noise_model = NoiseModel()
        noise_model.add_all_qubit_quantum_error(error_model, "measure")

        return noise_model
        
    def measure(self, pairs):
        double_matchings = []

        noise_model = None
        if self.depolarizing_probability > 0:
            noise_model = self.noise_model(self.depolarizing_probability)
        
        for i in range(len(pairs)):
            basis = randbits(1)
            if basis:
                # Measurement in "X" basis
                pairs[i][0].h(0)
                pairs[i][1].h(0)
                
            pairs[i][0].measure(0, 0)
            pairs[i][1].measure(0, 0)

            bits = ""
            for circuit in pairs[i]:
                transpiled = transpile(circuit, self.backend)
                results = self.backend.run(transpiled, noise_model = noise_model, shots = 1).result().get_counts()  
                bits += list(results.keys())[0]
            
            if bits[0] == bits[1]: double_matchings.append(i)
            
            self.measurement_results[i] = bits
            self.measurement_basis[i] = "X" if basis else "Z"
        
        return double_matchings

As can be seen, Bob introduces some noise to the circuits with a depolarizing error probability, to make it more realistic.

Step 3: The output of Bob.measure is the list of indices that resulted in a double matching. Bob also saves the measurements in measurements_results and the chosen basis in measurement_basis.

Step 4: Alice computes frames based on 2-combinations of the double matching indices:

    def public_frame_to_private_frame(self, frame):
        return (self.pairs_data[frame[0]], self.pairs_data[frame[1]])

    def compute_frames(self, double_matchings):
        usable_frames = {}
        auxiliary_frames = {}
        
        public_frames = list(combinations(double_matchings, 2))

        for public_frame in public_frames:
            private_frame = self.public_frame_to_private_frame(public_frame)

            if private_frame in self.usable_frames_iterable:
                usable_frames[public_frame] = self.usable_frames[private_frame]
            
            elif private_frame in self.auxiliary_frames_iterable:
                auxiliary_frames[public_frame] = self.auxiliary_frames[private_frame]  

        frames = list(usable_frames.keys()) + list(auxiliary_frames.keys())
        
        shuffle(frames)

        return frames, usable_frames, auxiliary_frames

Step 5: Alice shuffles the frames list, although this doesn’t increase security, in my opinion. Then, they are sent to Bob.

Step 6: Now Bob uses compute_sifting_strings to compute both the sifting bits and the measurement bits:

    def compute_sifting_bits(self, frame):
        sifting_bits = {
            "X": 0, 
            "Z": 0
        }
        
        for pair in frame:
            sifting_bits[self.measurement_basis[pair]] ^= int(self.measurement_results[pair][0])
            
        return ''.join(map(str, sifting_bits.values()))

    def compute_measured_bits(self, frame):
        measured_bits = []

        for pair in frame:
            measured_bits.append(self.measurement_results[pair][0]) # since both bits are equal due to the double matching event  

        return ''.join(measured_bits)
            
    def compute_sifting_strings(self, frames):
        sifting_strings = {}

        for frame in frames:
            sifting_bits = self.compute_sifting_bits(frame)
            measured_bits = self.compute_measured_bits(frame)

            sifting_strings[frame] = f"{sifting_bits},{measured_bits}"

        return sifting_strings

These sifting strings are really interesting because they give too much information. First of all, sifting bits are the column-wise XOR of the measured pairs, considering only the values that are 100% correct, and the rest as 0. For instance,

$$ \text{Alice:} \begin{pmatrix} \ket{1_\mathrm{X}} & \ket{1_\mathrm{Z}} \\ \ket{0_\mathrm{X}} & \ket{1_\mathrm{Z}} \end{pmatrix} \longrightarrow \text{Bob:} \begin{Bmatrix} \mathrm{Z}\\ \mathrm{X} \end{Bmatrix} \longrightarrow \begin{pmatrix} - & \ket{1_\mathrm{Z}} \\ \ket{0_\mathrm{X}} & - \end{pmatrix} \longrightarrow \text{01} $$

On the other hand, the measured bits are simply $10$, in row order. Since both pairs are double matchings, the $-$ sign is not relevant. So, the sifting string in this example is 01,10.

Step 7: Alice performs error detection and correction on Bob’s sifting strings:

    def verify_undetected_error(self, pair, detection_frame, required_sifting_string, frame, auxiliary_frames, auxiliary_frames_iterable, sifting_string):  
        for auxiliary_frame in auxiliary_frames_iterable:
            if  (
                    frame[pair]                       == auxiliary_frame[0]      and 
                    auxiliary_frames[auxiliary_frame] == detection_frame         and 
                    sifting_string[auxiliary_frame]   == required_sifting_string
                ):

                return True

        return False
    
    def error_correction(self, usable_frames, auxiliary_frames, bob_sifting_strings):
        alice_sifting_strings = bob_sifting_strings.copy()
        
        ambiguous_frames = []

        usable_frames_iterable = list(usable_frames.keys())
        auxiliary_frames_iterable = list(auxiliary_frames.keys())

        for frame in usable_frames_iterable:
            if alice_sifting_strings[frame] in VALID_SS[usable_frames[frame]]:
                sifting_bits = alice_sifting_strings[frame][:2]

                if sifting_bits == "01" or sifting_bits == "10":
                    ambiguous_frames.append(frame)

                else:
                    pair, detection_frame, required_sifting_string, corrections = ERROR_CORRECTION_RULES[usable_frames[frame]]
                    
                    verify = self.verify_undetected_error(
                                pair, 
                                detection_frame, 
                                required_sifting_string, 
                                frame, 
                                auxiliary_frames,
                                auxiliary_frames_iterable, 
                                alice_sifting_strings
                            )

                    if verify:
                        if  alice_sifting_strings[frame] == "00,11":
                            alice_sifting_strings[frame] = corrections[0]
                            
                        elif alice_sifting_strings[frame] == "11,11":
                             alice_sifting_strings[frame] = corrections[1]

            else:
                ambiguous_frames.append(frame)

        ambiguous_frames += auxiliary_frames

        shuffle(ambiguous_frames)
        
        return alice_sifting_strings, ambiguous_frames

This process is meant to discard frames that result ambiguous due to errors when measuring qbits on the simulated circuits. With this, Alice gets the correct sifting strings, that can be used to compute the shared secret. Bob also needs to know the frames that are ambiguous, in order to discard them later.

Step 8: Alice and Bob can generate the same secret:

    def generate_shared_key(self, frames, usable_frames, ambiguous_frames, alice_sifting_strings, bob_sifting_strings):  
        shared_secret = ""

        for frame in frames:
            if frame in ambiguous_frames:
                continue

            else:
                sifting_bits = alice_sifting_strings[frame][:2]
                measurement_result = ALICE_MR_DERIVATION[usable_frames[frame]][sifting_bits]
                shared_secret += KEY_DERIVATION[bob_sifting_strings[frame]][measurement_result]
        
        return shared_secret

    def generate_shared_key(self, frames, ambiguous_frames, sifting_strings):
        shared_secret = ""

        for frame in frames:
            if frame in ambiguous_frames:
                continue

            else:
                basis_orientation = (self.measurement_basis[frame[0]], self.measurement_basis[frame[1]])  
                measurement_result = BOB_MR_DERIVATION[basis_orientation]
                shared_secret += KEY_DERIVATION[sifting_strings[frame]][measurement_result]

        return shared_secret

Alice’s way to generate the secret looks more complicated. On Bob’s side, he only takes the measurement basis he computed at random and uses that to derive the secret using a table that depends on the measurement results.

Solution

I started playing with Alice and Bob in the Python REPL, with a small key size:

$ python3 -q
>>> from server import Alice, Bob, QKD
>>>
>>> while True:
...     qkd = QKD(Alice, Bob, 16, 8)
...     public = qkd.execute()
...     if 'error' not in public:
...         break
...
>>> public
{'double_matchings': [2, 3, 4, 6, 7, 8, 9, 11, 12, 13, 14, 15], 'frames': [(2, 15), (3, 13), (7, 12), (4, 14), (4, 7), (4, 6), (7, 13), (3, 12), (9, 15), (8, 15), (6, 15), (8, 13), (9, 13), (4, 9), (12, 15), (4, 8), (2, 13), (7, 15), (2, 4), (11, 12), (6, 12), (11, 15), (8, 12), (6, 13), (3, 15), (13, 15), (2, 12), (12, 13), (11, 13), (9, 12), (4, 11), (3, 4), (14, 15)], 'sifting_strings': ['11,11', '01,10', '00,11', '10,10', '11,11', '00,11', '01,10', '00,11', '11,11', '10,01', '00,11', '00,00', '01,10', '11,11', '11,11', '10,10', '01,10', '11,11', '11,11', '11,11', '11,11', '00,11', '01,01', '10,10', '11,11', '10,01', '00,11', '01,10', '10,10', '00,11', '00,11', '11,11', '10,01'], 'ambiguous_frames': [(7, 12), (13, 15), (9, 12), (11, 13), (3, 12), (3, 13), (8, 15), (12, 15), (11, 12), (14, 15), (2, 13), (7, 13), (8, 12), (4, 8), (4, 14), (9, 13), (2, 12), (6, 12), (6, 13), (12, 13), (8, 13)]}  
>>>
>>> double_matchings = public.get('double_matchings')
>>> frames = list(map(tuple, data.get('frames', [])))
>>> sifting_strings = public.get('sifting_strings')
>>> ambiguous_frames = set(map(tuple, public.get('ambiguous_frames', [])))
>>>
>>> double_matchings
[2, 3, 4, 6, 7, 8, 9, 11, 12, 13, 14, 15]
>>> frames
[(2, 15), (3, 13), (7, 12), (4, 14), (4, 7), (4, 6), (7, 13), (3, 12), (9, 15), (8, 15), (6, 15), (8, 13), (9, 13), (4, 9), (12, 15), (4, 8), (2, 13), (7, 15), (2, 4), (11, 12), (6, 12), (11, 15), (8, 12), (6, 13), (3, 15), (13, 15), (2, 12), (12, 13), (11, 13), (9, 12), (4, 11), (3, 4), (14, 15)]
>>> sifting_strings
['11,11', '01,10', '00,11', '10,10', '11,11', '00,11', '01,10', '00,11', '11,11', '10,01', '00,11', '00,00', '01,10', '11,11', '11,11', '10,10', '01,10', '11,11', '11,11', '11,11', '11,11', '00,11', '01,01', '10,10', '11,11', '10,01', '00,11', '01,10', '10,10', '00,11', '00,11', '11,11', '10,01']
>>> ambiguous_frames
{(6, 12), (12, 13), (3, 13), (8, 12), (8, 15), (7, 13), (4, 8), (4, 14), (12, 15), (3, 12), (14, 15), (9, 13), (11, 13), (2, 13), (6, 13), (7, 12), (9, 12), (11, 12), (8, 13), (2, 12), (13, 15)}

Let’s start looking at some values that we are not supposed to know. For instance, the variable bob_sifting_strings is computed from compute_sifting_strings on frames (I’ll put a beginning underscore to denote private variables):

>>> _bob_sifting_strings = qkd.Bob.compute_sifting_strings(frames)
>>> _bob_sifting_strings
{(2, 15): '11,11', (3, 13): '01,10', (7, 12): '00,11', (4, 14): '10,10', (4, 7): '11,11', (4, 6): '00,11', (7, 13): '01,10', (3, 12): '00,11', (9, 15): '11,11', (8, 15): '10,01', (6, 15): '00,11', (8, 13): '00,00', (9, 13): '01,10', (4, 9): '11,11', (12, 15): '11,11', (4, 8): '10,10', (2, 13): '01,10', (7, 15): '11,11', (2, 4): '11,11', (11, 12): '11,11', (6, 12): '11,11', (11, 15): '00,11', (8, 12): '01,01', (6, 13): '10,10', (3, 15): '11,11', (13, 15): '10,01', (2, 12): '00,11', (12, 13): '01,10', (11, 13): '10,10', (9, 12): '00,11', (4, 11): '00,11', (3, 4): '11,11', (14, 15): '10,01'}

Notice that we can get this value by joining frames and sifting_strings:

>>> dict(zip(frames, sifting_strings)) == _bob_sifting_strings  
True
>>> bob_sifting_strings = dict(zip(frames, sifting_strings))

Another thing to notice is that the bit-length of the shared key equals the length of frames minus the length of ambiguous_frames:

>>> _shared_key = qkd.shared_key
>>> _shared_key
b'010001000000'
>>> len(_shared_key)
12
>>> len(frames)
33
>>> len(ambiguous_frames)
21
>>> len(frames) - len(ambiguous_frames) == len(_shared_key)  
True

We know that none of the ambiguous_frames are used to generate the shared secret, therefore, we can easily find the frames that are actually used to generate the secret (which determines the length of the secret):

>>> used = sorted(set(frames).difference(ambiguous_frames))
>>> used
[(2, 4), (2, 15), (3, 4), (3, 15), (4, 6), (4, 7), (4, 9), (4, 11), (6, 15), (7, 15), (9, 15), (11, 15)]

Let’s take a closer look to the condition that makes a frame ambiguous or not:

    def error_correction(self, usable_frames, auxiliary_frames, bob_sifting_strings):  
        alice_sifting_strings = bob_sifting_strings.copy()
        
        ambiguous_frames = []

        usable_frames_iterable = list(usable_frames.keys())
        auxiliary_frames_iterable = list(auxiliary_frames.keys())

        for frame in usable_frames_iterable:
            if alice_sifting_strings[frame] in VALID_SS[usable_frames[frame]]:
                sifting_bits = alice_sifting_strings[frame][:2]

                if sifting_bits == "01" or sifting_bits == "10":
                    ambiguous_frames.append(frame)

                else:
                    # ...

            else:
                ambiguous_frames.append(frame)

        ambiguous_frames += auxiliary_frames

        shuffle(ambiguous_frames)
        
        return alice_sifting_strings, ambiguous_frames

We can see that sifting bits $01$ or $10$ are always ambiguous! Let’s have a look:

>>> bob_sifting_strings
{(2, 15): '11,11', (3, 13): '01,10', (7, 12): '00,11', (4, 14): '10,10', (4, 7): '11,11', (4, 6): '00,11', (7, 13): '01,10', (3, 12): '00,11', (9, 15): '11,11', (8, 15): '10,01', (6, 15): '00,11', (8, 13): '00,00', (9, 13): '01,10', (4, 9): '11,11', (12, 15): '11,11', (4, 8): '10,10', (2, 13): '01,10', (7, 15): '11,11', (2, 4): '11,11', (11, 12): '11,11', (6, 12): '11,11', (11, 15): '00,11', (8, 12): '01,01', (6, 13): '10,10', (3, 15): '11,11', (13, 15): '10,01', (2, 12): '00,11', (12, 13): '01,10', (11, 13): '10,10', (9, 12): '00,11', (4, 11): '00,11', (3, 4): '11,11', (14, 15): '10,01'}  
>>> ambiguous_frames
{(6, 12), (12, 13), (3, 13), (8, 12), (8, 15), (7, 13), (4, 8), (4, 14), (12, 15), (3, 12), (14, 15), (9, 13), (11, 13), (2, 13), (6, 13), (7, 12), (9, 12), (11, 12), (8, 13), (2, 12), (13, 15)}
>>> for t, s in bob_sifting_strings.items():
...     print(t, ' \t', repr(s), '\t', t in ambiguous_frames)
...
(2, 15)          '11,11'         False
(3, 13)          '01,10'         True
(7, 12)          '00,11'         True
(4, 14)          '10,10'         True
(4, 7)           '11,11'         False
(4, 6)           '00,11'         False
(7, 13)          '01,10'         True
(3, 12)          '00,11'         True
(9, 15)          '11,11'         False
(8, 15)          '10,01'         True
(6, 15)          '00,11'         False
(8, 13)          '00,00'         True
(9, 13)          '01,10'         True
(4, 9)           '11,11'         False
(12, 15)         '11,11'         True
(4, 8)           '10,10'         True
(2, 13)          '01,10'         True
(7, 15)          '11,11'         False
(2, 4)           '11,11'         False
(11, 12)         '11,11'         True
(6, 12)          '11,11'         True
(11, 15)         '00,11'         False
(8, 12)          '01,01'         True
(6, 13)          '10,10'         True
(3, 15)          '11,11'         False
(13, 15)         '10,01'         True
(2, 12)          '00,11'         True
(12, 13)         '01,10'         True
(11, 13)         '10,10'         True
(9, 12)          '00,11'         True
(4, 11)          '00,11'         False
(3, 4)           '11,11'         False
(14, 15)         '10,01'         True

It looks correct, all sifting strings that start with 01 or 10 are ambiguous. Therefore, these are the non-ambiguous frames:

>>> non_ambiguous = {t: s for t, s in bob_sifting_strings.items() if s[:2] in {'00', '11'}}
>>> non_ambiguous
{(2, 15): '11,11', (7, 12): '00,11', (4, 7): '11,11', (4, 6): '00,11', (3, 12): '00,11', (9, 15): '11,11', (6, 15): '00,11', (8, 13): '00,00', (4, 9): '11,11', (12, 15): '11,11', (7, 15): '11,11', (2, 4): '11,11', (11, 12): '11,11', (6, 12): '11,11', (11, 15): '00,11', (3, 15): '11,11', (2, 12): '00,11', (9, 12): '00,11', (4, 11): '00,11', (3, 4): '11,11'}

However, we need to take the frames that were actually used:

>>> used_non_ambiguous = {t: s for t, s in non_ambiguous.items() if t in used}
>>> used_non_ambiguous
{(2, 15): '11,11', (4, 7): '11,11', (4, 6): '00,11', (9, 15): '11,11', (6, 15): '00,11', (4, 9): '11,11', (7, 15): '11,11', (2, 4): '11,11', (11, 15): '00,11', (3, 15): '11,11', (4, 11): '00,11', (3, 4): '11,11'}  
>>>
>>> for t, s in used_non_ambiguous.items():
...     print(t, ' \t', repr(s))
...
(2, 15)          '11,11'
(4, 7)           '11,11'
(4, 6)           '00,11'
(9, 15)          '11,11'
(6, 15)          '00,11'
(4, 9)           '11,11'
(7, 15)          '11,11'
(2, 4)           '11,11'
(11, 15)         '00,11'
(3, 15)          '11,11'
(4, 11)          '00,11'
(3, 4)           '11,11'

This is very interesting. All used sifting strings are either 00,11 or 11,11… Let’s have a look at Bob’s measurement basis:

>>> for i, b in qkd.Bob.measurement_basis.items():  
...     print(f'{i:2d}: {b}')
...
 0: Z
 1: Z
 2: Z
 3: Z
 4: X
 5: Z
 6: X
 7: Z
 8: Z
 9: Z
10: X
11: X
12: Z
13: Z
14: X
15: X

Don’t you notice something? Let’s combine the outputs:

>>> for t, s in used_non_ambiguous.items():
...     print(t, ' \t', repr(s), '\t', (_basis[t[0]], _basis[t[1]]))  
...
(2, 15)          '11,11'         ('Z', 'X')
(4, 7)           '11,11'         ('X', 'Z')
(4, 6)           '00,11'         ('X', 'X')
(9, 15)          '11,11'         ('Z', 'X')
(6, 15)          '00,11'         ('X', 'X')
(4, 9)           '11,11'         ('X', 'Z')
(7, 15)          '11,11'         ('Z', 'X')
(2, 4)           '11,11'         ('Z', 'X')
(11, 15)         '00,11'         ('X', 'X')
(3, 15)          '11,11'         ('Z', 'X')
(4, 11)          '00,11'         ('X', 'X')
(3, 4)           '11,11'         ('Z', 'X')

Hey! If a sifting string is 11,11, then the basis are always $(\mathrm{Z}, \mathrm{X})$ or $(\mathrm{X}, \mathrm{Z})$. On the other hand, if the sifting string is 00,11, then the basis are always $(\mathrm{Z}, \mathrm{Z})$ or $(\mathrm{X}, \mathrm{X})$.

With this information, we can simply choose an initial basis for one index and then derive the rest using the previous conditions. We can do this with a simple algorithm:

basis = {used[0][0]: 'X'}

while len(basis) < len(used):
    old_basis = basis.copy()

    for u, m in old_basis.items():
        for t, v in used_non_ambiguous.items():
            if u == t[0] and v == '11,11' and t[1] not in basis:
                basis[t[1]] = 'Z' if m == 'X' else 'X'
            elif u == t[1] and v == '11,11' and t[0] not in basis:  
                basis[t[0]] = 'Z' if m == 'X' else 'X'
            elif u == t[0] and v == '00,11' and t[1] not in basis:
                basis[t[1]] = m
            elif u == t[1] and v == '00,11' and t[0] not in basis:
                basis[t[0]] = m

    if len(old_basis) == len(basis):
        break

We will have a 50% chance of getting the correct basis:

>>> basis = {used[0][0]: 'X'}
>>>
>>> while len(basis) < len(used):
...     old_basis = basis.copy()
...     for u, m in old_basis.items():
...         for t, v in used_non_ambiguous.items():
...             if u == t[0] and v == '11,11' and t[1] not in basis:
...                 basis[t[1]] = 'Z' if m == 'X' else 'X'
...             elif u == t[1] and v == '11,11' and t[0] not in basis:
...                 basis[t[0]] = 'Z' if m == 'X' else 'X'
...             elif u == t[0] and v == '00,11' and t[1] not in basis:
...                 basis[t[1]] = m
...             elif u == t[1] and v == '00,11' and t[0] not in basis:
...                 basis[t[0]] = m
...     if len(old_basis) == len(basis):
...         break
...
>>> basis_x = basis
>>> basis_x
{2: 'X', 15: 'Z', 4: 'Z', 9: 'X', 6: 'Z', 7: 'X', 11: 'Z', 3: 'X'}
>>> _basis
{0: 'Z', 1: 'Z', 2: 'Z', 3: 'Z', 4: 'X', 5: 'Z', 6: 'X', 7: 'Z', 8: 'Z', 9: 'Z', 10: 'X', 11: 'X', 12: 'Z', 13: 'Z', 14: 'X', 15: 'X'}

So, if the key is not correct, then it is the opposite:

>>> basis = {used[0][0]: 'Z'}
>>>
>>> while len(basis) < len(used):
...     old_basis = basis.copy()
...     for u, m in old_basis.items():
...         for t, v in used_non_ambiguous.items():
...             if u == t[0] and v == '11,11' and t[1] not in basis:
...                 basis[t[1]] = 'Z' if m == 'X' else 'X'
...             elif u == t[1] and v == '11,11' and t[0] not in basis:
...                 basis[t[0]] = 'Z' if m == 'X' else 'X'
...             elif u == t[0] and v == '00,11' and t[1] not in basis:
...                 basis[t[1]] = m
...             elif u == t[1] and v == '00,11' and t[0] not in basis:
...                 basis[t[0]] = m
...     if len(old_basis) == len(basis):
...         break
...
>>> basis_z = basis
>>> basis_z
{2: 'Z', 15: 'X', 4: 'X', 9: 'Z', 6: 'X', 7: 'Z', 11: 'X', 3: 'Z'}
>>> _basis
{0: 'Z', 1: 'Z', 2: 'Z', 3: 'Z', 4: 'X', 5: 'Z', 6: 'X', 7: 'Z', 8: 'Z', 9: 'Z', 10: 'X', 11: 'X', 12: 'Z', 13: 'Z', 14: 'X', 15: 'X'}

Notice that we don’t need to find the whole measurement basis, only the indices that are actually used for secret generation. Now, we can use Bob’s generate_shared_key to find the shared key:

>>> from helpers import BOB_MR_DERIVATION, KEY_DERIVATION
>>>
>>> def generate_shared_key(measurement_basis, frames, ambiguous_frames, sifting_strings):  
...     shared_secret = ''
...     for frame in frames:
...         if frame in ambiguous_frames:
...             continue
...         basis_orientation = (measurement_basis[frame[0]], measurement_basis[frame[1]])
...         measurement_result = BOB_MR_DERIVATION[basis_orientation]
...         shared_secret += KEY_DERIVATION[sifting_strings[frame]][measurement_result]
...     return shared_secret
...
>>> generate_shared_key(basis_x, frames, ambiguous_frames, bob_sifting_strings)
'101110111111'
>>> generate_shared_key(basis_z, frames, ambiguous_frames, bob_sifting_strings)
'010001000000'
>>> _shared_key.decode()
'010001000000'

At this point, we have found a way to find the shared key with a 50% chance.

Getting the flag

Now we only need use the shared key to derive an AES key to encrypt the requested command ("OPEN THE GATE"):

    while True:
        try:
            data = json.loads(input("> "))
            encrypted_command = bytes.fromhex(data["command"])
            assert len(encrypted_command) % 16 == 0
        except:
            json_print({"error": "Invalid input. Please, try again"})
            continue

        command = qkd.decrypt_command(encrypted_command)
        
        if command == "OPEN THE GATE":
            FLAG = open('flag.txt').read()
            json_print({"info": f" Welcome to The Frontier Board, the coordinates of The Starry Spurr are {SECRET_MESSAGE}{FLAG}"})  
            exit()

        else:
            json_print({"error": "Unknown command. Please, try again"})

The decrypt_command function uses the shared key to derive an AES key. Then, it removes PKCS7 padding, but there is no exception handler:

    def decrypt_command(self, encrypted_command):
        key = sha256(self.shared_key).digest()

        cipher = AES.new(key, AES.MODE_ECB)
        command = unpad(cipher.decrypt(encrypted_command), 16)  
    
        return command.decode()

Therefore, we won’t be able to test the two possible shared keys we got before, because it is very likely that a wrong AES key will result in incorrect padding and the server will close. But this is not a problem, because we will get the correct shared key one out of two times.

Flag

We can sum up all the above code snippets into a Python script that connects to the challenge instance, takes the needed information, extracts the shared key and uses it to encrypt the required command. With this, we can get the flag:

$ python3 solve.py 94.237.54.253:46816
[+] Opening connection to 94.237.54.253 on port 46816: Done
[+] Shared key: 0101010011011010111110011110011111111101011111101000010100101111110110001011100011011111010010011100010010101111010110110011010000101111001010001001101101011101101101111101001011101110110100101101011001000110010111100101110110010110010011101001111101100010101101111001100100110110011011100011000111100000011001000111110100100010100001011100011011110001110010100110101010101000111010001111111000000111000010101110110111101000010010101100001111010101001101010111011110100110111000010010100111101110111010110100100000000010011000001110001101111000000110001011100111001011101010110000010010110011110000101101000011011011110111101001101010011110100000111011010000110101100000010010001011100011101110101100111101111101111110101000100010100011101111110011010001001110  
[+] HTB{n0w_7h475_4_C1u7Ch!_d3f1n3731Y_Fr4m3_b453d_QKD_n33d5_70_M47ur3__C0ngr47u14710n5!_d546b1cc16212e806fac3136509fe5f8}
[*] Closed connection to 94.237.54.253 port 46816

The full script can be found in here: solve.py.

Conclusion

Not all research papers are perfect. This is a great example of an algorithm that looks pretty complex and hard to break, but it is fully broken, despite being very nicely documented. I want to thank the author of the challenge, D-Cryp7, for this awesome challenge, that made my deep-dive into the QKD protocol trying to find a flaw, although it seemed to be pretty secure at first glance.