Mind your Ps and Qs
1 minute to read
We are given the output of an RSA encryption:
Decrypt my super sick RSA:
c: 240986837130071017759137533082982207147971245672412893755780400885108149004760496
n: 831416828080417866340504968188990032810316193533653516022175784399720141076262857
e: 65537
RSA background
RSA works so that, given a message
And the decryption needs two more values:
Vulnerability
The modulus
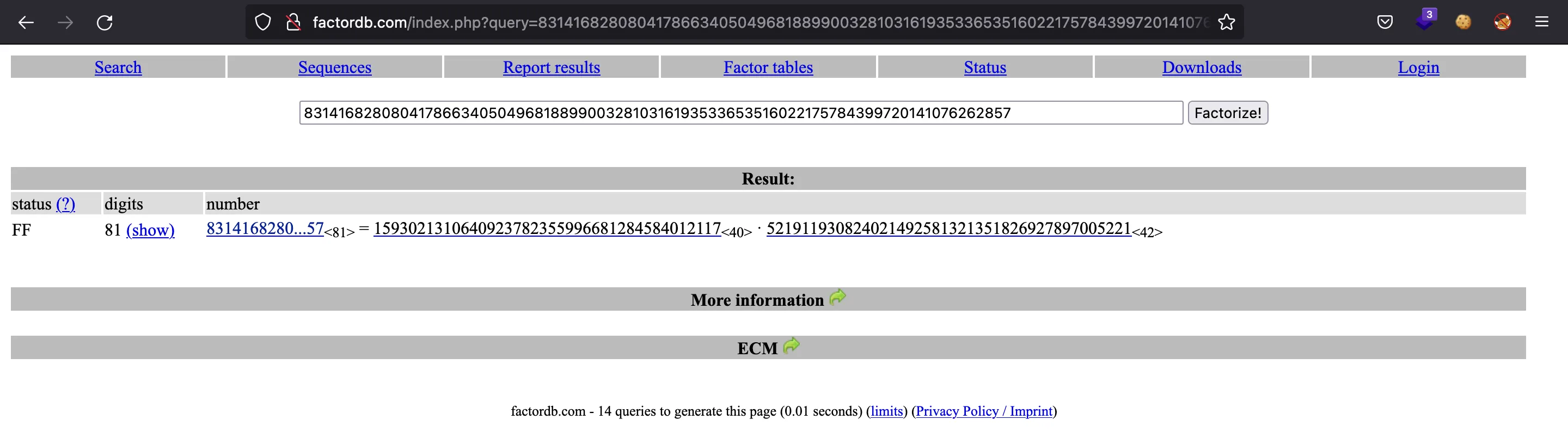
Having
Flag
$ python3 -q
>>> c = 240986837130071017759137533082982207147971245672412893755780400885108149004760496
>>> n = 831416828080417866340504968188990032810316193533653516022175784399720141076262857
>>> e = 65537
>>> p = 1593021310640923782355996681284584012117
>>> q = 521911930824021492581321351826927897005221
>>> assert n == p * q
>>> phi_n = (p - 1) * (q - 1)
>>> d = pow(e, -1, phi_n)
>>> m = pow(c, d, n)
>>> bytes.fromhex(hex(m)[2:])
b'picoCTF{sma11_N_n0_g0od_23540368}'